牛客练习-凤凰——不同寻常的最短路(找规律求结点数)

Posted 2022-02-05 C+++++++++++++++++++

文章目录

• • 题目六：凤凰
  • • 题目分析
    • 解题代码
    • • 法一：建树dfs
      • 法二：并查集

题目六：凤凰

题目链接

题目分析

这题我开始以为就是一个从1点开始的最短路算法，然后用了各种最短路算法也没过，后面发现原来是有这个"堵车"的限制！

注意由于题目是n个点，配备n-1条边，一般是不会存在环的！

以下为堵车情况的手写分析与证明结论的过程：

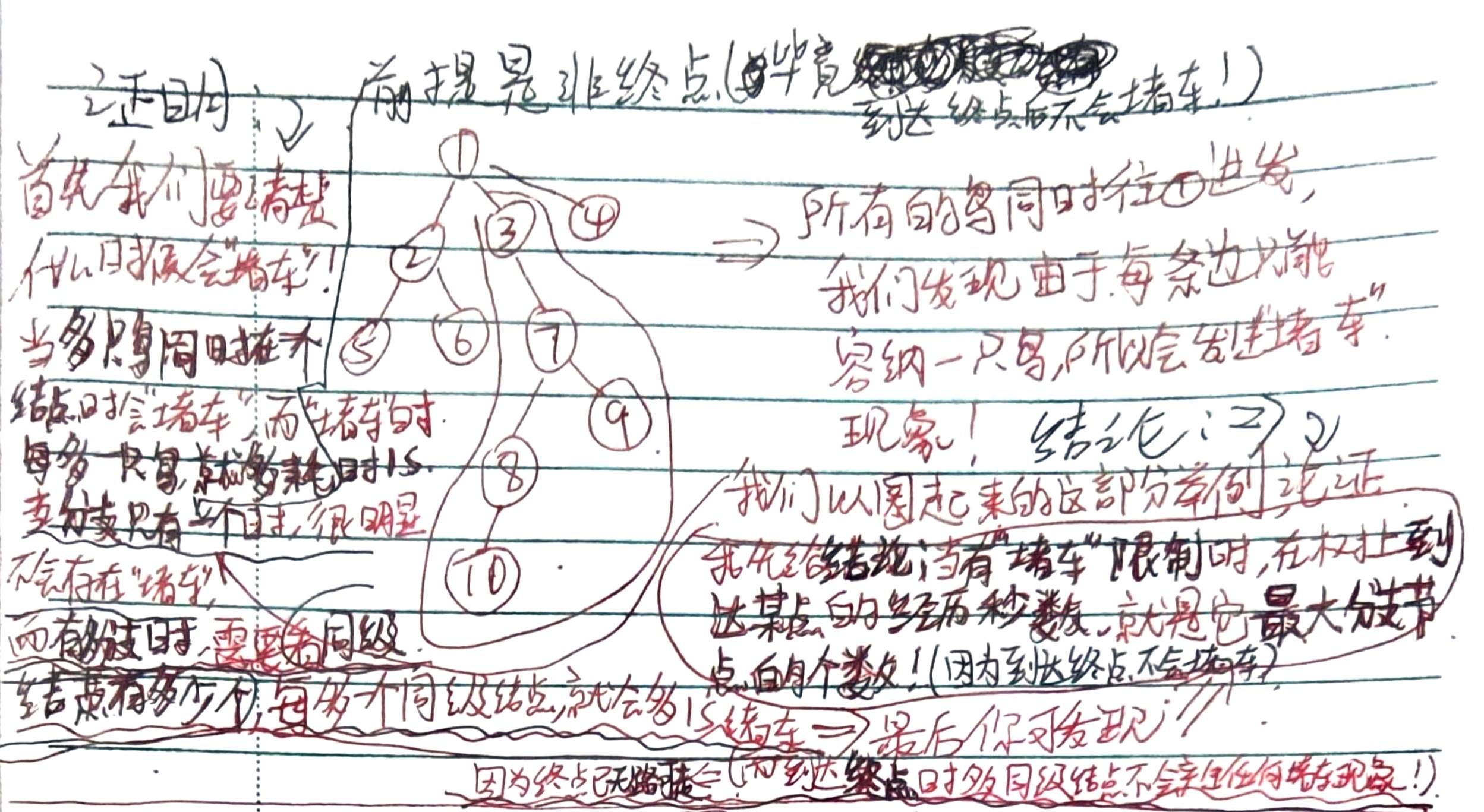
得出结论：

当有"堵车"限制之后，在树上到达某点经历的时间，就是该点分支的最大结点数。

所以实际上求到达1结点的时间，就是它所有子树的最大结点个数！

对于直接的计算树中结点个数我们有多种方法。

1. 建树，然后dfs计算。时间复杂度O(n)
2. 通过并查集分堆，然后得到所有堆里面的最多个数。时间复杂度O(logn)

解题代码

法一：建树dfs

注意取消同步，否则过不了

#include <bits/stdc++.h>
using namespace std;
vector<int>*graph;
int dfs(int cur_node,int pre_node)
    int res = 1;
    for (int i = 0; i < graph[cur_node].size(); ++i) 
        if(graph[cur_node][i]!=pre_node)
        res += dfs(graph[cur_node][i],cur_node);
    
    return res;

int main()
    ios::sync_with_stdio(false);
    int n;
    cin>>n;
    graph = new vector<int>[n];
    int a,b;
    for (int i = 1; i <n ; ++i) 
       cin>>a>>b;
       graph[a-1].push_back(b-1);
       graph[b-1].push_back(a-1);
    
    int res = INT_MIN;
    for (int j = 0; j < graph[0].size(); ++j) 
        res = max(res,dfs(graph[0][j],0));
    
    cout<<res;
    return 0;

法二：并查集

并查集过程只需要，把根去掉，然后整个树连在一起的就是一个分支。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
//TODO 实现并查集数据结构
class UnionFind
    int* root;
// 添加了 rank 数组来记录每个顶点的高度，也就是每个顶点的「秩」
    int* rank;
    int length;
public:
    ll* cnt;
    ll ret;
    UnionFind(int size):length(size)
        root = new int[size];
        rank = new int[size];
        cnt = new ll[size];
        for(int i=0;i<length;i++)
            root[i] = i;
            rank[i] = 1;
            cnt[i]=1;
        
        ret = 1;
    
    int find(int x)
        if(x==root[x])
            return x;
        return root[x]=find(root[x]);
    
// 按秩合并优化的 merge 函数
    void merge(int x,int y)
        int rootX = find(x);
        int rootY = find(y);
        //高度小的树被高度大的合并，如果高度一致合并后高度增加
        if(rootX!=rootY)
            if(rank[rootX]>rank[rootY])
                root[rootY] = rootX;
             else if(rank[rootX]<rank[rootY])
                root[rootX] = rootY;
            else
                root[rootY] = rootX;
                rank[rootX]++;
            
            ll sum_cnt = cnt[rootX] +cnt[rootY];
            cnt[rootX] = cnt[rootY] = sum_cnt;
            ret = max(ret,sum_cnt);
        
    
;
int main()
    int n;
    cin>>n;
    UnionFind uf(n+1);
    int m = n-1;
    int a,b;
    while (m--)
        cin>>a>>b;
        if(a==1||b==1)
            continue;
        uf.merge(a,b);
    
    cout<<uf.ret;
    return 0;