每日算法练习

Posted 2022-02-03 没谱的曲

1、删除链表的倒数第N个结点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：
给定一个链表: 1->2->3->4->5, 和 n = 2.

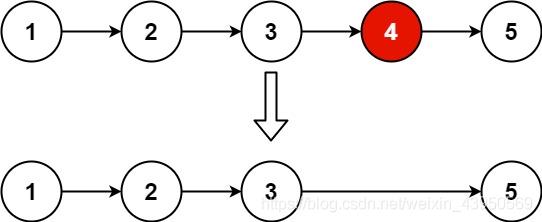
当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：给定的 n 保证是有效的。

提升：使用栈实现或使用双指针实现

解析：

该题我选择使用双指针来解决，首先我们建立一个链表结构

public class ListNode 
        int val;
        ListNode next;

        ListNode() 
        

        ListNode(int val) 
            this.val = val;
        

        ListNode(int val, ListNode next) 
            this.val = val;
            this.next = next;
        
    

我们先创建一个虚拟头结点，然后创建p1、p2两个指针初始值为虚拟头结点

ListNode fictitious = new ListNode(-1);
        fictitious.next = head;

        ListNode p1 = fictitious;
        ListNode p2 = fictitious;

我们先让p1走n+1个节点，之后再让p1和p2两个指针同时移动，直到p1指针指向末尾（此时p2节点指向的就是删除节点的上一个节点）

for (int i = 0; i < n ; i++) //p1节点先走n+1步
            p1 = p1.next;
        
        // 记住 待删除节点p2 的上一节点
        ListNode prev = null;
        while (p1 != null) //两个节点同时移动直到p1节点走到链表的末尾
            prev = p2;
            p2 = p2.next;
            p1 = p1.next;
        

最后，删除链表的倒数第N个节点，输出链表

// 上一节点的next指针绕过 待删除节点p2 直接指向p2的下一节点
        prev.next = p2.next;
        // 释放 待删除节点p2 的next指针
        p2.next = null;

        return fictitious.next;

完整代码如下：

public class DeleteN 
    public class ListNode 
        int val;
        ListNode next;

        ListNode() 
        

        ListNode(int val) 
            this.val = val;
        

        ListNode(int val, ListNode next) 
            this.val = val;
            this.next = next;
        
    

    public ListNode removeNthFromEnd(ListNode head, int n) 
        ListNode fictitious = new ListNode(-1);
        fictitious.next = head;

        ListNode p1 = fictitious;
        ListNode p2 = fictitious;
        for (int i = 0; i < n ; i++) //p1节点先走n+1步
            p1 = p1.next;
        
        // 记住 待删除节点p2 的上一节点
        ListNode prev = null;
        while (p1 != null) //两个节点同时移动直到p1节点走到链表的末尾
            prev = p2;
            p2 = p2.next;
            p1 = p1.next;
        
        // 上一节点的next指针绕过 待删除节点p2 直接指向p2的下一节点
        prev.next = p2.next;
        // 释放 待删除节点p2 的next指针
        p2.next = null;

        return fictitious.next;
    

2、在排序数组中查找数字（使用二分法）

统计一个数字在排序数组中出现的次数。

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

二分查找：

我们先来了解一下二分查找
直接在百度百科上查找，可以得出以下二分法的描述：

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

解析：

该题的数组已经是排序好了的，整个数组都是单调递增，这样就能完美适用二分法。
我们首先定义一个开始下标和一个结束下标，分别指向第一个元素和最后一个元素，定义一个count来记录最后要输出的该数出现的次数

int start = 0;//定义数组开始下标
        int end = nums.length - 1;//定义数组结束下标
        int count = 0;//target出现的次数，默认为0

从数组中间将数组分成两份，读取中间的数，若查找的数大于中间的数，则将开始下标移动到中间，否则将结束下标移动到中间，直到两个下标重合

while (start < end) //当start不小于end时，说明位置重合，跳出循环
            int mid = (start + end) / 2;
            if (nums[mid] >= target) 
                end = mid;
             else if (nums[mid] < target) //将值小于target的所有数排除在下标start的元素前
                start = mid + 1;
            
        

从下标为start的元素开始往后遍历，直到遍历完整个数组或遍历到的值不等于target为止

while (start < nums.length && nums[start] == target) //从下标为start的元素开始往后遍历，直到遍历完整个数组或遍历到的值不等于target为止
            start++;
            count++;
        
        return count;

完成后的完整代码如下：

public class BinarySearch 
    public int search(int[] nums, int target) 
        int start = 0;//定义数组开始下标
        int end = nums.length - 1;//定义数组结束下标
        int count = 0;//target出现的次数，默认为0
        while (start < end) //当start不小于end时，说明位置重合，跳出循环
            int mid = (start + end) / 2;
            if (nums[mid] >= target) 
                end = mid;
             else if (nums[mid] < target) //将值小于target的所有数排除在下标start的元素前
                start = mid + 1;
            
        
        while (start < nums.length && nums[start] == target) //从下标为start的元素开始往后遍历，直到遍历完整个数组或遍历到的值不等于target为止
            start++;
            count++;
        
        return count;
    

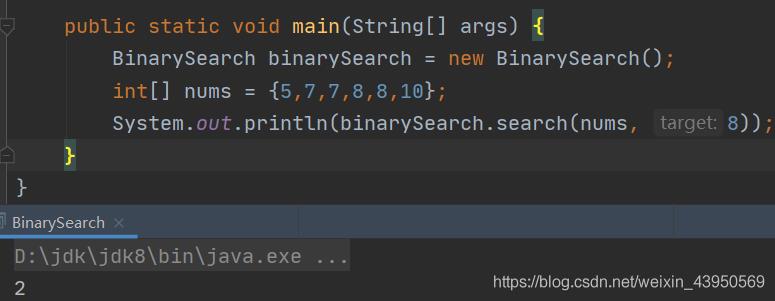
现在我们调用这个方法测试一下：

public static void main(String[] args) 
        BinarySearch binarySearch = new BinarySearch();
        int[] nums = 5,7,7,8,8,10;
        System.out.println(binarySearch.search(nums, 8));
    

测试结果：

3、用两个栈实现队列

用两个栈来实现一个队列，分别完成在队列尾部插入整数(push)和在队列头部删除整数(pop)的功能。
队列中的元素为int类型。保证操作合法，即保证pop操作时队列内已有元素。

示例:
输入:
[“PSH1”,“PSH2”,“POP”,“POP”]
返回:
1,2
解析:
“PSH1”:代表将1插入队列尾部
“PSH2”:代表将2插入队列尾部
"POP“:代表删除一个元素，先进先出=>返回1
"POP“:代表删除一个元素，先进先出=>返回2

解析：

该题看似困难，其实分析后就会感觉非常简单
我们首先要了解栈和队列的关系：

• 栈：是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
• 队列：队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

简单来说，栈就是只有一个口，这个口不仅是入口也是出口，先入后出，后入先出
而队列有两个口，一个为入口，一个为出口，只能先从入口存数据，才能从出口出，先入先出，后入后出
那么我们要如何通过两个栈来实现队列呢？
首先我们创建两个栈

Stack<Integer> stack1;
    Stack<Integer> stack2;
    public CQueue() 
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    

我们将一个栈用来实现插入操作，而另一个栈用来实现输出操作。
当我们要进行插入操作的时候直接调用方法往第一个栈中存数据

    public void psh(int value) 
        stack1.add(value);
    

当我们要进行删除操作的时候

1. 如果stack2为空，我们就将stack1中的所有元素取出，存入stack2中
2. 如果stack2仍为空，返回-1，否则从stack2中弹出一个值

public int pop() 
        if (stack2.isEmpty()) 
            if (stack1.isEmpty()) return -1;
            while (!stack1.isEmpty()) 
                stack2.add(stack1.pop());
            
            return stack2.pop();
         else return stack2.pop();
    

完成后的完整代码如下：

import java.util.Stack;

public class CQueue 

    Stack<Integer> stack1;
    Stack<Integer> stack2;
    public CQueue() 
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    


    public void psh(int value) 
        stack1.add(value);
    

    public int pop() 
        if (stack2.isEmpty()) 
            if (stack1.isEmpty()) return -1;
            while (!stack1.isEmpty()) 
                stack2.add(stack1.pop());
            
            return stack2.pop();
         else return stack2.pop();
    

调用两个方法测试一下

public static void main(String[] args) 
        CQueue cQueue = new CQueue();
        cQueue.psh(1);
        cQueue.psh(2);
        System.out.println(cQueue.pop());
        System.out.println(cQueue.pop());
    

测试结果：

算法之路漫漫，多加练习，才能提升自己！