LeetCodeLeetCode之跳跃游戏Ⅱ——暴力解法+动态规划+贪婪算法

Posted 2022-02-02 Roninaxious

1.题目描述

🔐给你一个非负整数数组 nums ，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。

⌛示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

⌛示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

❗提示:

1 <= nums.length <= 104
0 <= nums[i] <= 1000

2.暴力解题思路

💎反向查找，我们可以考虑最后一步前的位置，因此我们可以考虑最后一步跳跃前所在的位置，该位置通过跳跃能够到达最后一个位置。你可能我会说如果有多个能够达到最后一个位置，该怎么选择呢？我们肯定会选择距离最后一个位置最远的那一个。

• 从下标0开始遍历，当遍历到下标为2的时候发现能够达到最后一个位置，所以此时讲end置为下标2
• 从下标0开始遍历，发现下标0能到达end，结束
• 结果就为2

3.暴力解法代码

public static int jump2(int[] nums) 
        int size = nums.length;
        if (size == 1) 
            return 0;
        
        int minJumps = 0;
        for (int i = 0; i < size; i++) 
            if (size == 2) 
                minJumps++;
                break;
            
            if (nums[i] + i >= size - 1) 
                minJumps++;
                size = i + 1;
                i = -1;
            
        
        return minJumps;
    

复杂度分析

时间复杂度：O(n^2)
空间复杂度：O(1)

提交到LeetCode会发现超出时间限制。

4.动态规划思路

本题的核心是最少的跳跃次数，其实我们应该首先想到的是动态规划，首先就是如何分解子问题？

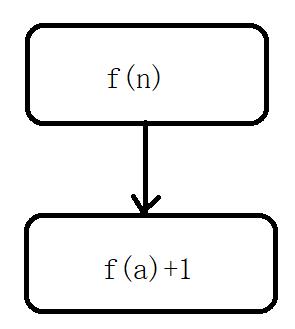
📑求解f(n)无非就是求距离最后一个位置最远且可达的位置+1。那么它的dp[i]就代表当前位置的最少跳跃次数。转移方程那肯定就是dp[n]=dp[a]+1，a就代表距离n最远的那个位置的下标。【由于这个a是无法直接确定的，所以需要一个内层循环提供支持】

5.动态规划解题代码

    public static int jump(int[] nums) 
        int[] dp = new int[nums.length];
        dp[0] = 0;
        for (int i = 1; i < nums.length; i++) 
            for (int j = 0; j < i; j++) 
                if (nums[j] + j >= i) 
                    dp[i] = dp[j] + 1;
                    break;
                
            
        
        return dp[nums.length - 1];
    

复杂度分析

时间复杂度：O(n^2)
空间复杂度：O(n)

不过庆幸的是提交到LeetCode能通过，但也很极限

我们可以发现本题使用动态规划，有很多重复的比较，这种就接近递归了，无法做到很大的优化。那有没有一种能达到时间复杂度为O(n)的方法呢？

6.贪婪算法解题思路

📅我们都知道贪心算法具有贪心选择性，从一个状态转移到另一个状态，不会对后续造成影响，往往具有唯一的最优选择。所以本题我们可以长期维护一个最远跳跃距离maxPos，遍历数组，每遍历一个元素就更改其最远跳跃距离maxPos，当达到临界值end时，将当前最远跳跃maxPos赋值给临界值end并将跳跃次数+1.

7.贪婪算法解题代码

    public static int jump3(int[] nums) 
        int length = nums.length;
        int maxPos = 0;
        int rb = 0;
        int time = 0;
        for (int i = 0; i < length - 1; i++) 
            maxPos = Math.max(maxPos, nums[i] + i);
             if (i == rb) 
                rb = maxPos;
                time++;
            
        
        return time;
    

复杂度分析：

时间复杂度：O(n)
空间复杂度：O(1)

提交到LeetCode