数字信号处理6：IIR滤波器设计

Posted 2022-01-31 zuguorui

IIR滤波器设计

文章目录

• IIR滤波器设计
• • 1. 简介
  • 2. 设计步骤简明
  • 3. 拉普拉斯变换和Z变换
  • • 3.1 拉普拉斯变换
    • 3.2 Z变换
  • 4. 双线性变换法
  • • 4.1 模拟域与数字域的映射
    • 4.2 模拟滤波器的性能指标
    • • 4.2.1 基本参数定义
      • 4.2.2 巴特沃兹滤波器阶数公式
      • 4.2.3 切比雪夫I型和II型滤波器阶数公式
      • 4.2.4 椭圆滤波器阶数公式
  • 5. 三种模拟滤波器原型
  • 6. 从模拟低通滤波器构造模拟高通、带通、带阻滤波器
  • • 6.1 模拟高通滤波器设计
    • 6.2 模拟带通滤波器设计
    • 6.3 模拟带阻滤波器设计
  • 7. IIR滤波器设计步骤总结
  • 8. 使用Matlab设计IIR滤波器
  • 9. 有限字长效应

1. 简介

IIR滤波器（无限冲激响应滤波器）相比FIR（有限冲激响应滤波器），是一种在运算效率方面非常高效的滤波器，相比于FIR滤波器，在实现同等的滤波效果时，IIR滤波器所需的阶数要比FIR滤波器低很多。FIR滤波器的阶数一方面取决于通带与阻带之间的增益（低阶滤波器应用高增益，会导致吉布斯效应），一方面取决于滤波精度（FIR滤波器的精度为$F_s/N$，$F_s$为采样率，$N$为滤波器阶数）。而IIR滤波器阶数一方面也是由通带和阻带之间的增益差决影响的，一方面则是由通带与阻带之间的频率的比值决定。但是IIR滤波器有两个缺点：相位响应不是线性的；阶数过高时难以稳定。

通常，定义一个线性时不变系统的传输函数如下：

$$\begin{gathered} y[n]=b[0]x[n]+b[1]x[n-1]+\cdots +b[N]x[n-N]+ \\ a[1]y[n-1]+a[2]y[n-2]+\cdots +a[M]y[n-M]\text{\hspace{1em}(1)} \end{gathered}$$

对于FIR滤波器来说，输出只与输入有关，即$a[n]=0$，而IIR滤波器的输出不仅与输入有关，还与过去的输出有关，即$a[n]$不总是为0。

2. 设计步骤简明

IIR滤波器设计相比于FIR滤波器，所需的计算和步骤都更为复杂，很多书上开始讲这一点都从艰深的步骤开始，而对于我这样的数学不好的新手来说则是一头雾水。实际上在一开始掌握IIR滤波器设计的大体流程对于实用学习来说是非常有益的。接下来我就从工程实用的角度来大概说明IIR滤波器设计的几个重要方法和步骤。

1. 与FIR滤波器可以直接从频域设计频率响应然后通过傅里叶变换得到时域滤波器不同，IIR滤波器无法从时域直接设计响应，而是通过经典模拟滤波器转换而来。几种经典模拟滤波器分别是巴特沃兹滤波器、切比雪夫I型和II型滤波器、椭圆滤波器。而这几种滤波器都是有参考表的，可以根据滤波器阶数直接确定模拟滤波器系数。
2. 以上所得的模拟滤波器都是低通形式的，因此要采用一些方法将其转换为带通、带阻和高通滤波器。
3. 将上述转换后的不同形式的模拟滤波器转换成数字滤波器。转换的方法有冲激不变法、双线性变换法。最常用的是双线性变换法，这也是这篇博客所讲的方法。
4. 若要像FIR滤波器那样，针对不同频段有不同的增益，那么就需要将IIR滤波器进行串联或并联，后面我会讲一篇音频EQ的例子，它就是使用了IIR滤波器并联。

以上基本就是IIR滤波器的总结，其中出现了几个大家会在教材里经常见到的关键字。不过IIR滤波器和模拟滤波器相关，因此接下来首先要对拉普拉斯变换和Z变换有一个大概的认识。

3. 拉普拉斯变换和Z变换

这里只是简单让大家对这两种变换有个印象，不会具体讲理论。需要的同学可以查看其他教材。

3.1 拉普拉斯变换

定义拉普拉斯变换如下：

$$X(s)={\int }_{-\infty }^{+\infty }x(t)e^{-st}\text{\hspace{1em}(2)}$$

其中，$s=\sigma +j\Omega$。

拉普拉斯变换是描述模拟域的。如果将$\sigma$和$w$分别作为平面坐标系的x轴和y轴，这个平面就是我们定义的s平面。

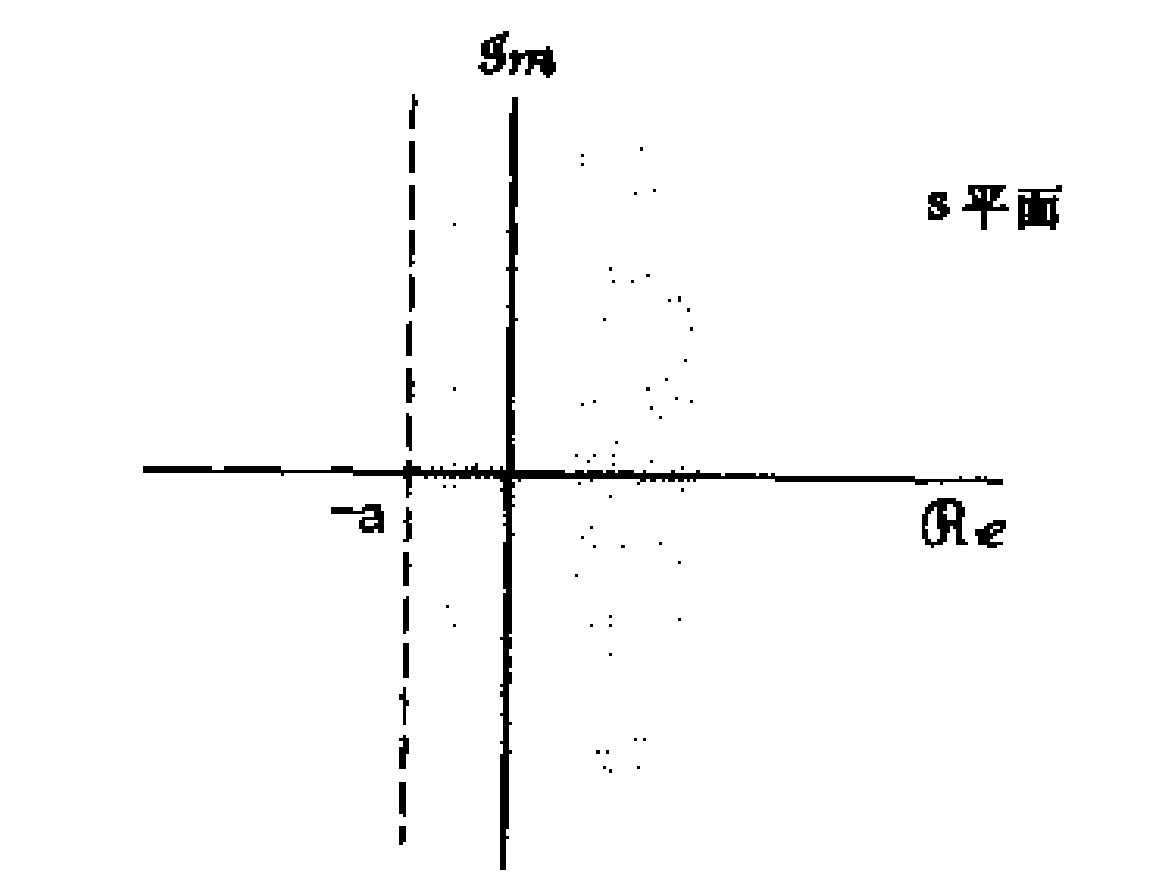
可以看到，拉普拉斯变换实际上就是为将信号幅值增益为原来的$e^{\sigma }$倍。如果$\sigma =0$，则特化为连续信号的傅里叶变换，落在s平面上就是虚轴。

一个信号的拉普拉斯变换是有收敛域的。如果x(t)的拉普拉斯变换是有理的，如果x(t)是右边信号，那么其收敛域ROC就位于s平面上最右边极点的右边。如果x(t)是左边信号，那么其收敛域就位于s平面上最左边极点的左边。 我们实际处理的信号都是有理的且为右边信号，因此适用于第一种情况。
关于更详细的拉普拉斯变换的知识，可以参考奥本海默的《信号与系统》。

3.2 Z变换

定义Z变换为

$$X[z]=\sum _{n=-\infty }^{+\infty }x[n]z^{-n}\text{\hspace{1em}(3)}$$

其中，$z=r{e}^{jw}$。
若将$r$看作$z$的幅值，$w$看作$z$的相角，则两者的关系可看作是一个极坐标表示的平面，称为z平面。

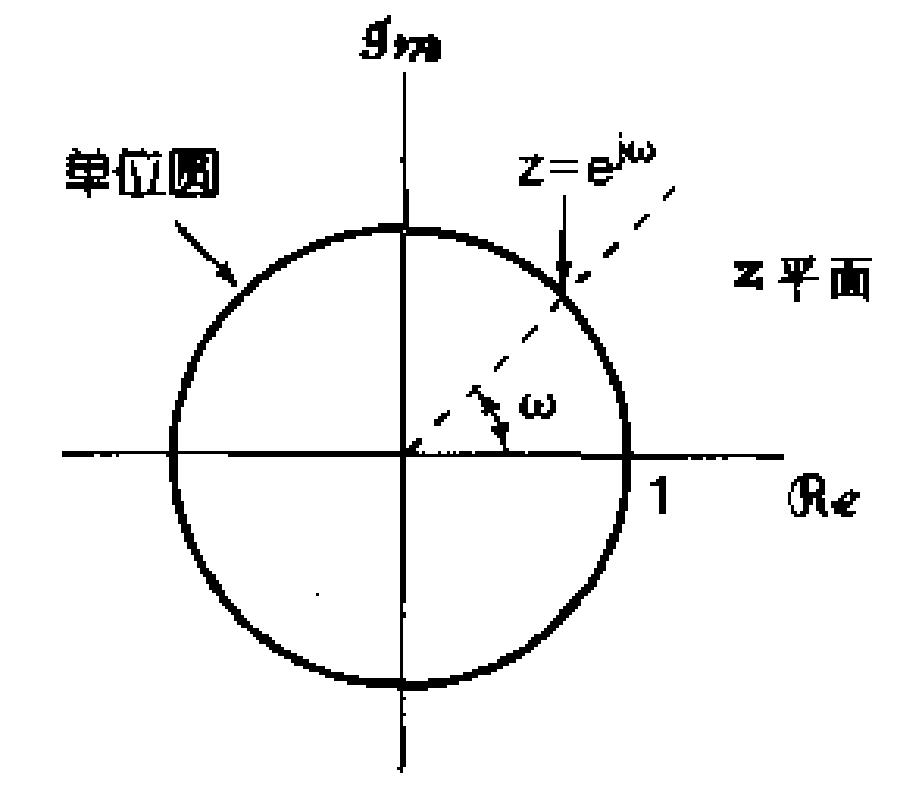
和拉普拉斯变换一致，可以看作是将信号$x[n]$的幅值增大到$r$倍。如果$r=0$，那么就特化离散信号的傅里叶变换，落在z平面的单位圆上。

基于Z变换，我们可以将数字域LTI系统的转换方程用两个多项式的比来表示。
首先，基于以下推导：

$$\begin{gathered} Z(x[n-k])=\sum _{n=-\infty }^{+\infty }x[n-k]z^{-n}=\sum _{n=-\infty }^{+\infty }x[n-k]z^{-(n-k)}{z}^{-k} \\ =z^{-k}\sum _{n=-\infty }^{+\infty }x[n-k]z^{-(n-k)}=z^{-k}X[z] \end{gathered}$$

应用到式1

$$\begin{gathered} y[n]=b[0]x[n]+b[1]x[n-1]+\cdots +b[N]x[n-N]+ \\ a[1]y[n-1]+a[2]y[n-2]+\cdots +a[M]y[n-M] \\ \Downarrow \\ Y[z]=b[0]X[z]+b[1]X[Z]z^{-1}+\cdots +b[N]X[z]z^{-N}+ \\ a[1以上是关于数字信号处理6：IIR滤波器设计的主要内容，如果未能解决你的问题，请参考以下文章 \end{gathered}$$

数字信号处理6：IIR滤波器设计

IIR数字滤波器的设计

IIR数字滤波器与FIR数字滤波器的定义？

实验六 基于MATLAB的IIR数字滤波器设计

实验六 基于MATLAB的IIR数字滤波器设计

滤波器设计模拟到数字