排序算法总结

Posted 2022-01-31 楊木木8023

1、直接插入排序

       (1) 分析：假设一个待排序集合A=a,b,c,d,e,f…，插入排序就是初始时将a视为只有一个元素的有序子集和B；从b开始，依次和集合B的元素比较，找到其插入的位置，最终的有序集合B即为排序的集合。直接排序的最坏情况的时间复杂度：O(n2)。

       (2) 应用场景：直接插入排序是稳定的，也就是说要排序的数中有两个相同的数，插入法进行排序后，两个相等数的位置不会互换，则A算法是稳定的，否则A不稳定，所以当实现一个排序且不想改变相对位置时可以使用直接插入排序。在大部分元素已排好序时，用直接插入排序较好。

       (3) 代码：

def insert_sort(nums):
    for i in range(1, len(nums)):
        key = nums[i]
        j = i - 1
        while j > 0 and key < nums[j]:
            nums[j+1] = nums[j]
            j -= 1
        nums[j+1] = key
return nums

2、折半插入排序

        (1) 分析：折半插入法相对于直接插入法减少了比较的次数，即当一个元素向前面的子集插入时，由于子集已经有序，所以寻找插入位置时进行折半查找。也就是，如果元素比子集的中间位置的元素大时，插入位置在子集的前一半中，如果元素比子集的中间位置小时，插入位置在子集的后一半。折半插入减少了插入元素的时间复杂度O(log2n)，但是由于元素移动部分的复杂度没变，所以折半插入排序的时间复杂度：O(n2)。

       (2) 应用场景：直折半插入排序是稳定的，所以当实现一个排序且不想改变相对位置时可以使用折半插入排序。

       (3) 代码：

def half_sort(nums):
    for i in range(1, len(nums)):
        key = nums[i]
        low = 0
        high = i-1
        while low <= high:
            mid = (high+low)//2
            if key < nums[mid]:
                high = mid - 1
            if key >= nums[mid]:
                low = mid + 1
        j = i-1
        while j >= low:
            nums[j+1] = nums[j]
            j -= 1
        nums[low] = key
return nums

3、冒泡排序

        (1) 分析：在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。每趟排序结束后，都会有一个元素找到自己最终在集合的位置。冒泡排序的时间复杂度：O(n2)。

       (2) 应用场景：冒泡排序是稳定的。

       最大数问题(179)：给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。如：nums=[3,30,34,5,9]，输出9534330。

       分析：用冒泡排序的方式进行解题，从前到后排序时，可以nums[i]和nums[i+1]的字符串和与nums[i+1]和nums[i]字符串的和的大小对比，例如330和303进行比较，然后进行冒泡排序，最终拼接成字符串就是最大数。

def largestNumber(self, nums) -> str:
    for i in range(0, len(nums)):
        for j in range(0, len(nums) - i - 1):
            if str(nums[j]) + str(nums[j + 1]) < str(nums[j + 1]) + str(nums[j]):
                nums[j + 1], nums[j] = nums[j] + nums[j + 1]
    nums = [str(i) for i in nums]
    res = "".join(nums)
    if int(''.join(nums)) == 0:
        return str(0)
    else:
        return ''.join(nums)

       (3) 代码：

def bubble_sort(nums):
    for i in range(0, len(nums)):
        for j in range(0, len(nums)-i-1):
            if nums[j] > nums[j+1]:
                nums[j], nums[j+1] = nums[j+1], nums[j]
    return nums

4、快速排序

        (1) 分析：选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描，将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素就找到了正确位置,然后再用同样的方法递归地排序划分的两部分，快速排序是一种原地排序。快速排序的时间复杂度：O(nlog2n)。

       (2) 应用场景：快速排序不稳定，适用于数据量大的情况。快排一次排序就有一个元素排在了对应的位置，所以可以用快排+分治加快查找速度。例如：数组中的第K个最大元素问题(215)。

       分析：数组a快排一次可以确定一个元素的最终位置q，并且a[0…..q-1]中的每个元素小于等于 a[q]，且 a[q]小于等于 a[q + 1 ……len(a)] 中的每个元素。所以，只要某次快排的q为倒数第K个下标的时候，就找到了答案，若q比倒数第K个下标小时，就在对a[0…..q-1]进行同样的快排，反之，则对a[q + 1 ……len(a)]进行快排。

def findKthLargest(self, nums, k: int) -> int:
    pos = len(nums) - k
    def repid_sort(nums, low, high):
        if low >= high:
            return nums[pos]
        i, j = low, high
        key = nums[i]
        while i < j:
            while i < j and key <= nums[j]:
                j -= 1
            nums[i] = nums[j]
            while i < j and key >= nums[i]:
                i += 1
            nums[j] = nums[i]
        nums[i] = key
        if i == pos:
            return key
        elif i > pos:
            return repid_sort(nums, low, i - 1)
        else:
            return repid_sort(nums, i + 1, high)
    return repid_sort(nums, 0, len(nums) - 1)

       (3) 代码：

def rapid_sort(nums, low, high):
    if low >= high:
        return nums
    i = low
    j = high
    key = nums[i]
    while i < j:
        while i < j and key <= nums[j]:
            j -= 1
        nums[i] = nums[j]
        while i < j and key >= nums[i]:
            i += 1
        nums[j] = nums[i]
    nums[i] = key
    rapid_sort(nums, low, i - 1)
rapid_sort(nums, i + 1, high)

5、选择排序

        (1) 分析：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。如果待排序集合有n个元素，那么一共要进行n-1次排序。选择排序的时间复杂度：O(n2)。

       (2) 应用场景：选择排序不稳定，适用于数据量小的情况。

       (3) 代码：

def choose_sort(nums):
    for i in range(0, len(nums)):
        min_position = i
        for j in range(i+1, len(nums)):
            if nums[j] < nums[min_position]:
                min_position = j
        if i != min_position:
            nums[i], nums[min_position] = nums[min_position], nums[i]
    return nums

6、堆排序

        (1) 分析：堆是具有以下性质的完全二叉树：每个父结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个父结点的值都小于或等于其左右孩子结点的值，称为小顶堆。堆排序的时间复杂度：O(nlogn)。

       (2) 应用场景：堆排序是不稳定的，适用于数据量大的情况，使用堆的好处主要在于数据不用一下读入内存中，比如topn问题。

        TopN问题(剑指offer40)：输入n个整数，输出其中最大的k个数？

        分析：堆的性质是每次可以找出最大或最小的元素。可以使用一个大小为 k 的小顶堆，将数组中的元素依次入堆，当堆的大小超过 k 时，便将多出的元素从堆顶弹出。也就是说，在小顶堆中，堆顶是最小的元素，先将集合的前k个元素入堆，从集合的k+1个元素开始，和堆顶进行比较，若大于堆顶元素则说明堆顶不是最大的k个之一，则将堆顶元素删除，进入新的元素；若小于堆顶元素则无需处理，直接跳过。最终，堆中的元素就是最大的k个元素。（反之，输出最小的k个数，利用大顶堆即可）

def getLeast1Numbers(self, arr, k):
    if len(arr) <= k:
        return arr
    heap = []
    for i in range(len(arr)):
        if i < k:
            heap.append(arr[i])
        else:
            heapq.heapify(heap)
            if heap[0] < arr[i]:
                heapq.heapreplace(heap, arr[i])
    return heap

        注意：在python中heapq默认为小顶堆，若要建大顶堆，可以将arr的所有数据先变为负数，即arr = [-i for i in arr]，然后其他部分不变，最后输出时，去掉负号。

       (3) 代码：

import heapq  # python默认的小顶堆
def heap_sort(nums):
    result = []
    for i in range(len(nums)):
        heapq.heapify(nums)  # 相当于将最小值找出，写入结果
        result.append(nums[0])
        nums.remove(nums[0])  # 把最小值删除，其余的部分继续按这样的步骤处理
    return result

排序总结：

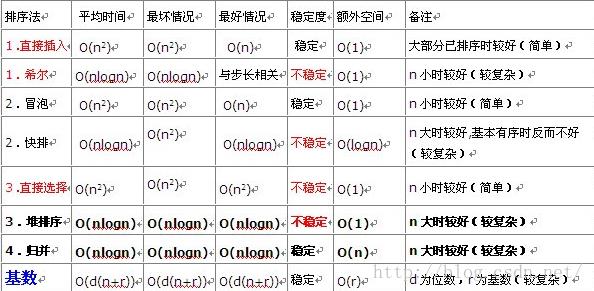
排序链表：

def sort_link(self, Node):
    firstNode = Node.next
    second_Node = firstNode
    while firstNode:
        while firstNode.next:
           if firstNode.element >firstNode.next.element:
              temp = firstNode.element
              firstNode.element=firstNode.next.element
                firstNode.next.element = temp
            firstNode = firstNode.next
        firstNode = second_Node.next
        second_Node = firstNode