用Python使用快速傅里叶变换分析振动传感器采集的数据并绘制趋势图分布图和频谱图

Posted 2022-01-28 bkzy

背景

某振动传感器可以通过蓝牙将测量的设备振动信号传输到手机，现需要对采集到的数据进行分析，并绘制趋势图、数据分布图和频谱图。
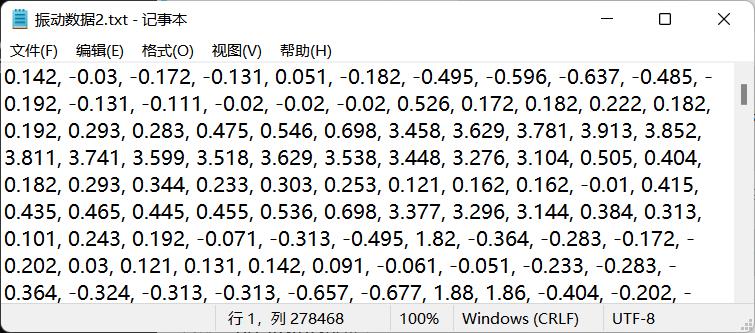
振动传感器的采样频率为12.8KHz（采样间隔为 1e6/12800=78.125微秒）,每秒钟最多可以将2048个（160ms的测量数据）数据传输到手机。采集获得的数据保存为文本文件，数据样式如下图。

环境

本文使用 python 3.9.6，在Windows 11环境下，用 jupyter notebook 进行分析。

读取数据文件

import numpy as np 
import pylab as pl #导入绘图模块
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']   #显示中文
mpl.rcParams['axes.unicode_minus']=False       #显示负号

# 通过文件读取数据
with open("振动数据2.txt", "r") as f:  # 打开文件
    data = f.read()  # 读取文件
# 文件重点数据使用逗号分隔，此处需要把数据分隔提取
data = data.split(',')
# 提取到的数据是文本格式的，需要转换为浮点数的数据
x = [float(v) for v in data]
print("共有%d点数据"%(len(x)))
"""
此处输出为：
共有38912点数据
"""

绘制趋势图和数据分布直方图

sampling_rate = 12800 #取样频率(来自传感器说明书)
fft_size = 2048 #FFT处理的数据样本数

# 用linspace计算每个数据点的时间标，时间标的单位为ms,总时长为160ms(2048个数据点)：
# linspace在指定的间隔内返回均匀间隔的数字
# np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
tstemp = np.linspace(0,int(1e6/sampling_rate * fft_size),fft_size)/1e3

# 绘制图形
pl.figure(figsize=(14,8))
pl.title("原始数据(趋势图)")
pl.ylabel("振动加速度(m/s2)")
pl.xlabel("时间(ms)")
pl.plot(tstemp,x[:fft_size])

pl.figure(figsize=(14,8))
pl.title("原始数据(分布图)")
pl.ylabel("点数")
pl.xlabel("振动加速度(m/s2)")
pl.hist(x[:fft_size],bins=100)
pl.show()

绘制的图形如下：

执行傅里叶变换

在np.fft中，有fft和rfft可以选择。
如果样本数据的总数量为N，fft函数返回N个变换后的数据，但是这N个数据是左右对称的，即有效的实际数据只有N/2+1个。
而rfft直接只返回N/2+1个数据，可以不用处理直接使用。

# 进行快速傅里叶变换
xs = x[:fft_size]# 从波形数据中取样fft_size个点进行运算
# 利用np.fft.rfft()进行FFT计算
# rfft返回N/2+1个数据。而fft返回N个数据，但这N个数据是左右对称的，因此实际有效的是N/2+1个数据。
# 所以此处直接使用rfft
xfft = np.fft.rfft(xs) 
# 打印显示前5个傅里叶转换结果
# 可以看出傅里叶转换结果是复数
# 复数用y=a+bj的形式表示，a为实部，b为虚部
print(xfft[:5])

此处的输出数据为

[2442.331       +0.j         -216.7047702  -55.99042361j
 -394.94605398-121.14476753j    8.80615719 +90.98250801j
  -65.84171697 +10.04387751j]

绘制频谱图

• 取频率
  绘制频谱图，首先一点试要知道横坐标上每点对应的频率值。
  本项目中的采样频率sampling_rage=12800Hz，共有N=fft_size=2048个采样点。
  将0~sampling_rage分为N份，然后将美分对应给各个数值，即使每个样本数据点所对应的频率。
  由于经过rfft傅里叶变换后，频率和样本点折半了，因此计算中频率使用sampling_range/2,样本点数使用N/2+1。

• 复数取模运算
  相当于始数取绝对值，但对于复数来说，没有绝对值这个概念。
  复数取模运算是对实部和虚部的平方和开根号，即：
  $$y=\sqrt{a^2+b^2}$$

# 通过下面的np.linspace计算出返回值中每个下标对应的真正的频率：
# 最后除以1e3将频率单位由Hz转换为KHz
freqs = np.linspace(0,int(sampling_rate/2),int(fft_size/2+1))/1e3

# 对复数取绝对值(取模运算)，复数的模为：√a^2 + b^2
abs_xfft=abs(xfft)

pl.figure(figsize=(14,8))
pl.title("单边振幅谱(未归一化)")
pl.ylabel("振幅(未归一化)")
pl.xlabel("频率(KHz)")
pl.plot(freqs,abs_xfft)
pl.show()

绘制的图形为：

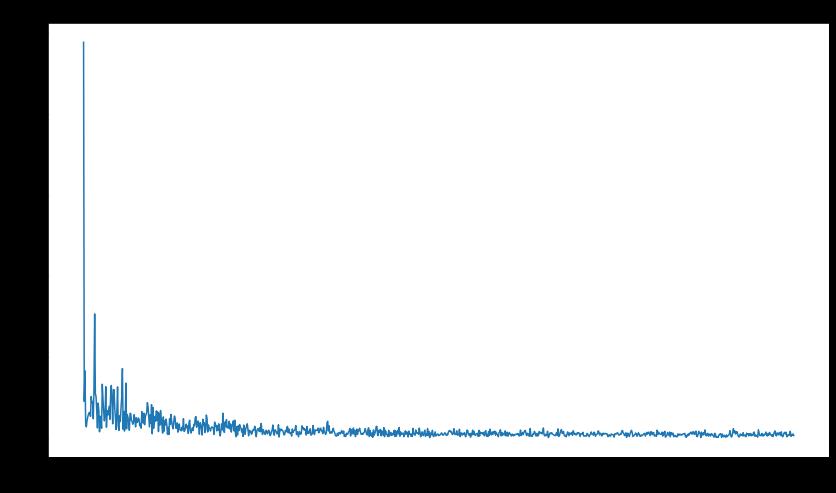
可以发现它的纵坐标非常大，看不出具体的物理意义。为了使纵坐标具有物理意义，工程应用中需要将取模后的傅里叶转换结果归一化，即将数值除以样本总数N.

数据归一化

# 直接对傅里叶转换后的结果进行归一化处理
# 归一化处理(可以在取模前归一化，也可以在取模后归一化)
abs_xfft_n = abs_xfft/fft_size

# 再次绘图
pl.figure(figsize=(14,8))
pl.title("单边振幅谱(归一化后)")
pl.ylabel("振动加速度(m/s2)")
pl.xlabel("频率(KHz)")
pl.plot(freqs,abs_xfft_n)
pl.show()

可以看到此时的图的纵坐标具备了一定的物理含义。但是最大值与最小值之间差别比较大，大值将小值压制的几乎只有一条线了，看不太清趋势。此时还可以对纵坐标的值取对数，缩小大值和小值之间的差别。但缺点是纵坐标的物理意义又不清楚了。

纵坐标取对数

# 对归一化取模后的数据再取以10为底的对数
# np.clip(a, a_min, a_max, out=None, **kwargs)
# np.clip将输入中a限制在min和max之间，将小于min的置为min，大于max的置为max
# 防止出现 log(0)导致无法计算的问题
xfft_log = np.log10(np.clip(abs_xfft_n,1e-20,1e1000))
pl.figure(figsize=(14,8))
pl.title("单边振幅谱(取Log10后)")
pl.ylabel("振动加速度(Log10(m/s2))")
pl.xlabel("频率(KHz)")
pl.plot(freqs,xfft_log)
pl.show()

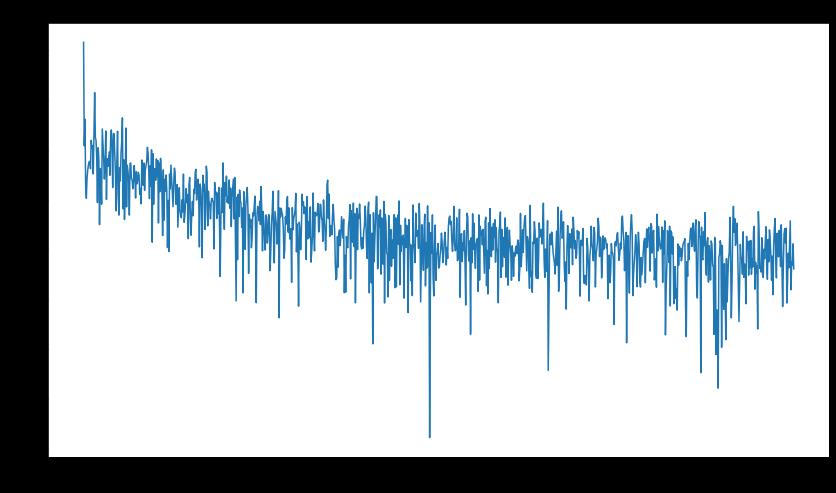
参考文献

python绘制频谱图_使用python进行傅里叶FFT-频谱分析详细教程
python画信号频谱(fft)