ACM - 贪心(经典母题+POJ一些练习题)
Posted 肆呀
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ACM - 贪心(经典母题+POJ一些练习题)相关的知识,希望对你有一定的参考价值。
总的来说,贪心就是对于求解最优解问题,每一步都做当前最优的措施,当然这需要子问题最优必定能推出总的最优才能这么做,不然很可能需要dp解决。
目前一点浅见,贪心更像是靠题感想到一种解决方案,然后先证明其合法性,再证明其不可能不是最优。
经典母题
这一部分主要照着AcWing上的题目写的笔记。
1、区间问题
AcWing 905. 区间选点
原题链接:https://www.acwing.com/problem/content/907/
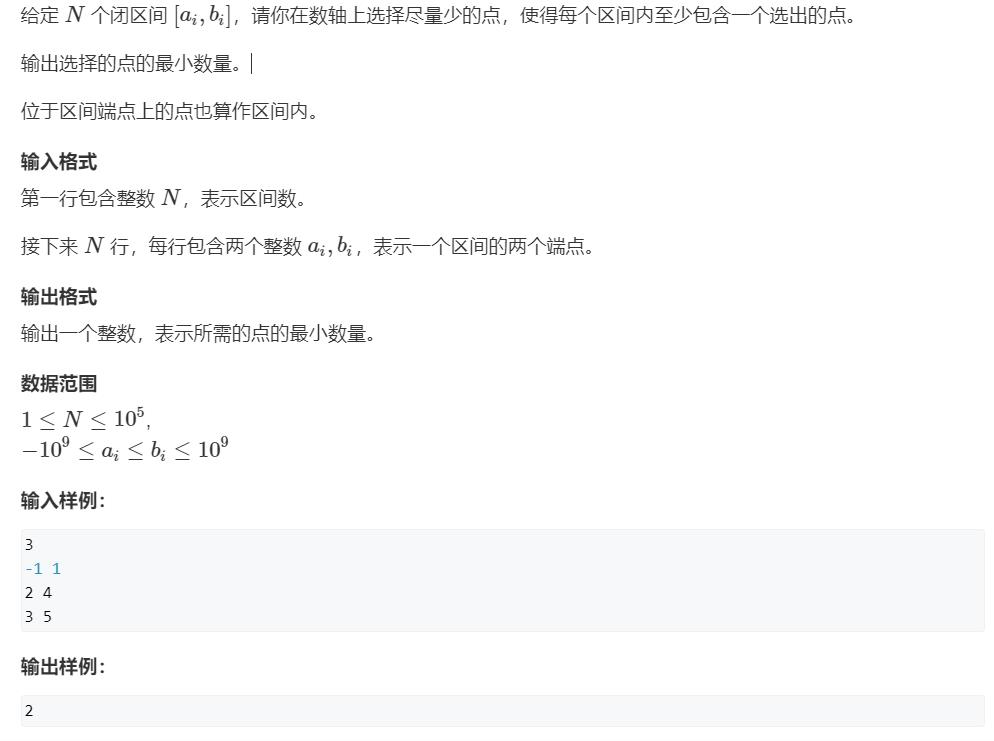
做法
按照右端点从小到大排序后,选择第一个区间的右端点 x ,若后续有区间 w 不能被 x 选中,则 ++ ans 的同时,更新 x 为 w 的右端点。
证明
采用 “贪心 >= 最优解 && 贪心 <= 最优解” 的方式得出 贪心 == 最优解。
① 贪心 >= 最优解
首先我们每当有一个区间 w 无法包含当前的 x 时,就会重新在 w 范围内找到一个点更新 x,故而可以保证贪心出来的解法是能够囊括所有区间的,即贪心是合法解,只是不确定是否一定最优。
② 贪心 <= 最优解
首先在该贪心策略下,每一次重新选 x 的时候,都意味着当前区间和上一次选 x 的区间是互相独立的、没有任何交集的,换而言之,将每一次会导致重新选 x 的区间抽离出来,这 a 个独立区间注定需要 a 个点,而 a 即为该贪心策略下需要重新选 x 的次数。换句话说,贪心 <= 最优解。
综上,贪心 == 最优解。
#include <bits/stdc++.h>
using namespace std;
#define getlen(array) return (sizeof(array) / sizeof(array[0]));
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 100010;
int dx[] = -1, 1, 0, 0, dy[] = 0, 0, -1, 1;
struct range
int l, r;
arr[N];
bool cmp(range a, range b)
return a.r < b.r;
int main()
//freopen("D:\\\\in.txt", "r", stdin);
//freopen("D:\\\\out.txt", "w", stdout);
rin;
for (int i = 0; i < n; ++ i)
rit;
ria;
arr[i] = t, a;
sort(arr, arr + n, cmp);
int cnt = 0, last = -INF;
for (int i = 0; i < n; ++ i)
if (arr[i].l > last)
last = arr[i].r;
++ cnt;
pr("%d", cnt);
return 0;
AcWing 908. 最大不相交区间数量
原题链接:https://www.acwing.com/problem/content/910/

做法
这道题和 AcWing 905. 区间选点 做法一样。
按照右端点从小到大排序后,选择第一个区间的右端点 x ,若后续有区间 w 不能被 x 选中,则 ++ ans 的同时,更新 x 为 w 的右端点。
证明
采用 “贪心 <= 最优解 && 贪心 不可能< 最优解” 的方式得出 贪心 == 最优解。
① 贪心 <= 最优解
首先我们每当有一个区间 w 无法包含当前的 x 时,就会重新在 w 范围内找到一个点更新 x,故而可以保证贪心出来的所有区间是互相不会覆盖的,即贪心是合法解,只是不确定是否一定最优。
② 贪心 < 最优解 是错的
假如存在最优解 > 贪心,设最优解为 a 个区间,贪心解法为 b 个区间,在最优解情况下,至少需要 a 个点才能把所有区间覆盖,但由上一题可知 b 个点就足以覆盖,故而 a 不可能 > b,即最优解不可能 > 贪心。
综上,贪心 == 最优解。
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
struct range
int l, r;
arr[N];
bool cmp(range a, range b)
return a.r < b.r;
int main()
cin >> n;
for (int i = 0; i < n; ++ i)
int a, b;
cin >> a >> b;
arr[i] = a, b;
sort(arr, arr + n, cmp);
int cnt = 0, last = -0x3f3f3f3f;
for (int i = 0; i < n; ++ i)
if (arr[i].l > last)
last = arr[i].r;
++ cnt;
cout << cnt;
return 0;
AcWing 906. 区间分组
原题链接:https://www.acwing.com/problem/content/908/
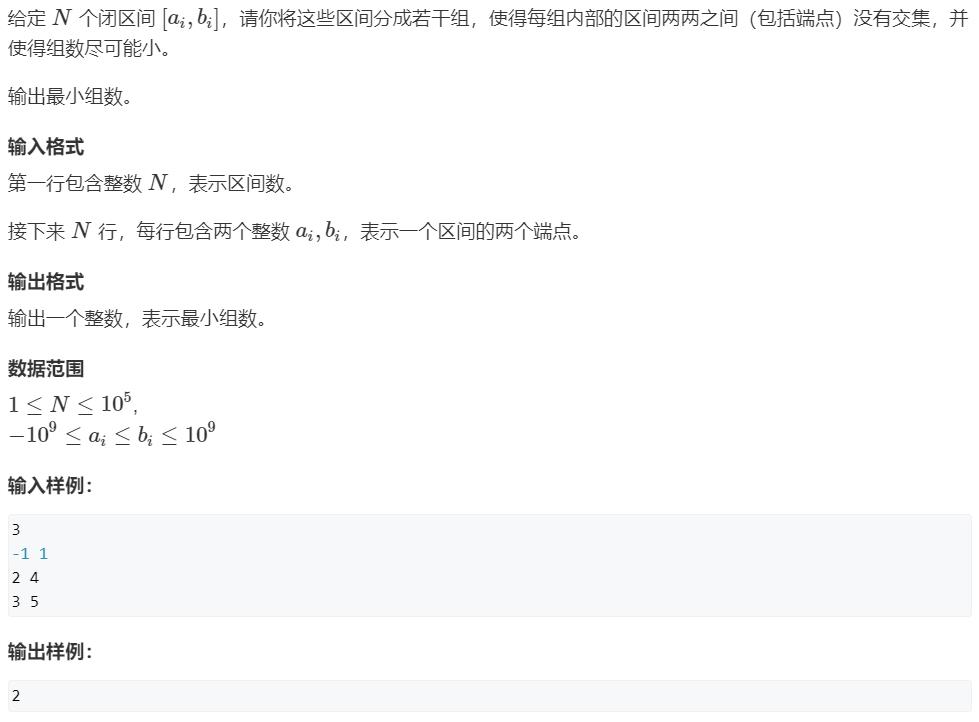
做法
将所有区间按照左端点从小到大排序,开一个小根堆,存每一组最右一个区间的右端点。
遍历区间数组,如果堆顶那一组能放下当前区间,则更新;不能则新开一组。
证明
① 合法性
首先,该种选法所确定的每一组都不会有区间重叠的情况,故而合法。
② 最优性
假如此时堆内有 a 组能容纳当前区间 x ,那么其实这些组中任意一组都可以放置当前区间 x。因为这些区间是按照左端点排序的,在 x 之后的任意一个区间 y (y的左端点大于等于x的左端点),想要放置在 a 中任意一组是更加没有问题的,所以并不存在说直接把堆顶那一组给 x 会影响到 y。
反之,如果连堆顶都容纳不下 x,那么其他现有的组是更加不可能的,所以需要新开一组。
#include <bits/stdc++.h>
using namespace std;
#define getlen(array) return (sizeof(array) / sizeof(array[0]));
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 100010;
int dx[] = -1, 1, 0, 0, dy[] = 0, 0, -1, 1;
struct range
int l, r;
;
range arr[N];
bool cmp(range a, range b)
return a.l < b.l;
int main()
//freopen("D:\\\\in.txt", "r", stdin);
//freopen("D:\\\\out.txt", "w", stdout);
rin;
// cout << " n == " << n << endl;
for (int i = 0; i < n; ++ i)
int a, b;
sc("%d%d", &a, &b);
arr[i] = a, b;
sort(arr, arr + n, cmp);
priority_queue<int, vector<int>, greater<int> > h;
for (int i = 0; i < n; ++ i)
range a = arr[i];
if (h.empty() || a.l <= h.top())
h.push(a.r);
else
h.pop();
h.push(a.r);
cout << h.size();
return 0;
AcWing 907. 区间覆盖
原题链接:https://www.acwing.com/problem/content/909/


做法
将左端点按从小到大排序,last 表示目标区间目前需要被覆盖的点,遍历区间数组,在能覆盖当前的 last 的区间中选择右端点最大的,然后更新 last 为该区间的右端点,循环往复,直到 last >= 目标区间的右端点。
证明
① 正确性
首先,这种做法一定能保证选出来的区间能把目标区间完全覆盖,或者所有区间本身并不能覆盖目标区间。
因为每一次选的是区间中右端点最大的,如果连最大的都无法覆盖,那么显然不存在合法方案。
② 最优性
假设存在比当前方案更少的区间数,那么聚焦于局部,那必然是存在类似于最优解中 2 个区间就能覆盖贪心解中 3 个甚至更多区间,那么这 2 个区间中必然会存在有的区间右端点比 3 个区间中的某部分区间更长,这与该贪心策略下做法矛盾。故而不存在更少的区间数。
#include <bits/stdc++.h>
using namespace std;
#define getlen(array) return (sizeof(array) / sizeof(array[0]));
#define ll long long
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 100010;
int dx[] = -1, 1, 0, 0, dy[] = 0, 0, -1, 1;
struct range
int l, r;
arr[N];
bool cmp(range a, range b)
return a.l < b.l;
int main()
//freopen("D:\\\\in.txt", "r", stdin);
//freopen("D:\\\\out.txt", "w", stdout);
int st, ed;
cin >> st >> ed;
int n;
cin >> n;
for (int i = 0; i < n; ++ i)
int a, b;
cin >> a >> b;
arr[i] = a, b;
sort(arr, arr + n, cmp);
bool flag = false;
int ans = 0, last = st;
for (int i = 0; i < n; ++ i)
range a = arr[i];
if (a.l <= last && a.r >= last)
++ ans;
int j = i, t = j;
while (j < n && arr[j].l <= last) //我是傻逼 忘了j < n调了好久的段错误
if (arr[t].r < arr[j].r) t = j;
++ j;
i = j - 1;
last = arr[t].r;
//这个if不可以放在外面,不然假设st == ed 那么会使得ans = 0就break
if (last >= ed)
flag = true;
break;
if (flag) cout << ans;
else cout << -1;
return 0;
2、Huffman树
AcWing 148. 合并果子
原题链接:https://www.acwing.com/problem/content/150/

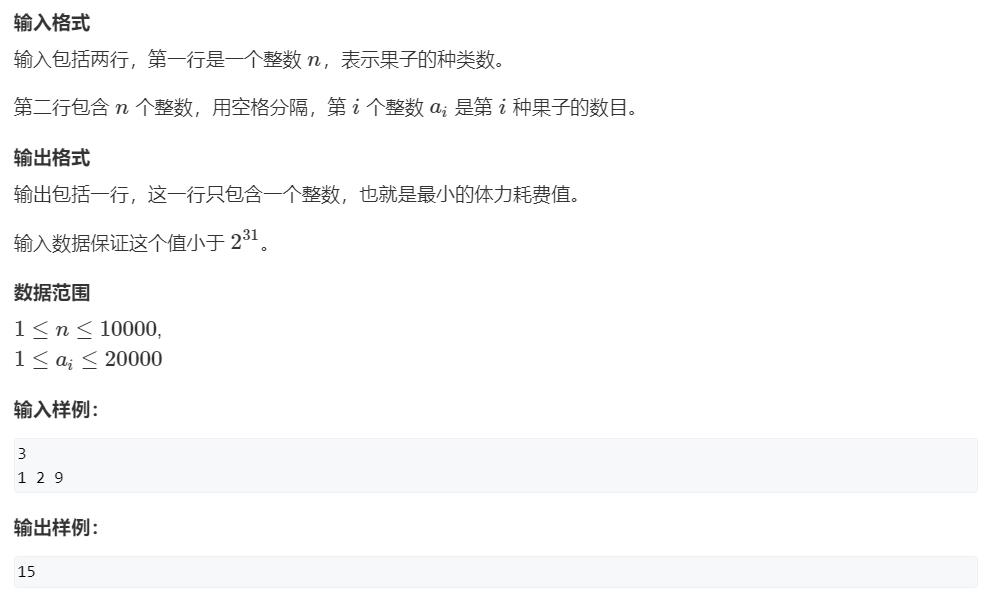
做法
因为不是必须相邻两堆,而是每次任意取两堆,所以其实就是构造哈夫曼树,每一次取倒数第一和第二小的合并后再放回去。
证明
简单一点来说,可以设 f(n)为合并 n 堆时的最小消耗值,那么 f(n) = f (n - 1)+ a + b。
每一次拿出最小和次小的两堆,保证了(a + b)是最小的,同时将(a + b)再次放回 f (n - 1)计算时,也是最优的做法(合并后的 a + b 和另一堆合并时,所消耗的是能做到的最小的方案)。
#include <bits/stdc++.h>
using namespace std;
#define getlen(array) return (sizeof(array) / sizeof(array[0]));
#define ll long long
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
int dx[] 以上是关于ACM - 贪心(经典母题+POJ一些练习题)的主要内容,如果未能解决你的问题,请参考以下文章