吴恩达_MIT_MachineLearning公开课ch02

Posted 2023-02-22 用七年单身换个PolyU.CSPhD

回顾回归

我们在ch01使用gradient descent[梯度下降]，实现了linear regression[回归]问题。
简单地来说，我们在读入数据后提取出X[Varibale,factors etc]作为我们的变量，或者说就是影响一个问题的一系列因素 和 Y[标签]问题的解。

我们定义了损失函数，函数只包含了变量theta，我们的目标就是用损失函数对theta进行求导，迭代更新不断缩小损失值直到最后收敛。

回归常可以用于的问题就是预测，比如原本数据中给你了一大堆影响房价的因素[X:Factors]以及对应因素下的真实房价[Y:Labels]，你就可以通过拟合出每种因素所占的权值从而对一组特定变量进行房价预测！

逻辑回归

我觉得逻辑回归之所以带了回归，就是因为其实际上也蕴含了“预测”的思想。
上述这一点在我们的作业中就很容易看出。

那实际上逻辑回归在机器学习中常用于处理“分类”问题。
最简单的就是二分类问题，比如给你一张图预测是猫or狗，当然了这是深度学习的问题我们的作业中用的是是否被一所学校录取作为二分类问题。(因为答案只有yes or no)

因为分类问题我们需要知道的属于某种情况的“概率问题”，概率嘛，当然不能为负，所以我们称之为“逻辑”。

解题步骤

我们同样是需要定义损失函数和一组待拟合的参数theta的。这里唯一需要注意的一点就是因为我们要输出一个非负值，也就是逻辑概率，所以我们在np.dot(X, theta)后需要用一个sigmoid激活函数进行激活。(否则这个值有可能求出来是负数！)

sigmoid是个长这样的函数(y = 1 / (1 + e^-x)):
这样一来我们的求出来的值不就压缩到(0, 1)范围内成为一个合理的概率了么？

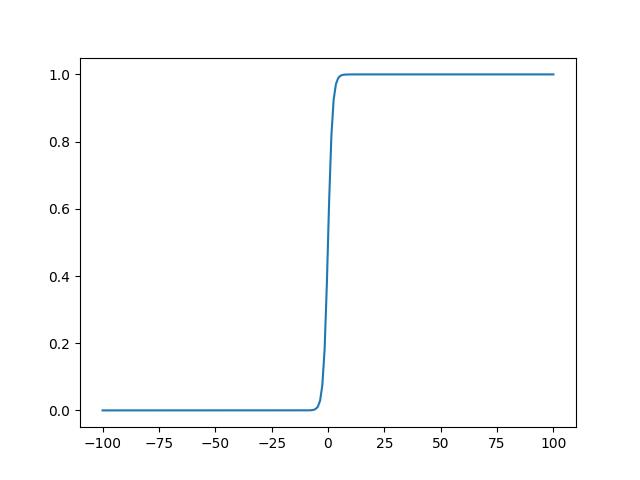
浅谈此函数的优缺点：
优点是函数连续易于求导，缺点是计算量较大且容易产生梯度消失问题(无法收敛)。

损失函数

损失函数有点长，我并不想手写打出来，直接用吴恩达老师在作业里给出的：
其中h(x)就是经过sigmoid激活的np.dot(X, theta)。

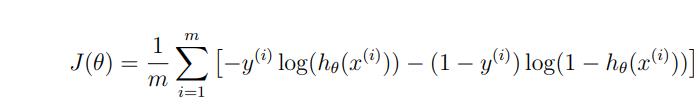
这个损失函数有个专有名叫做“交叉熵”，可以简单分析一下此函数的特点。
当y = 1时，退化为 -log(h(x))，此时若想要损失值尽可能小，那么h(x)应该无限趋近于1！若h(x)无限趋近于0，即和真实标签完全背道而行，损失值也是无限大的！
y = 0时是可以同理得到结果的，因此这个函数的设计是完全合理的！

上面只谈论其合理性，从根本上来解释可以看这个逻辑回归损失函数的理解或者看我下面这张从中截的图。

课后作业

我们的课堂作业的数据如下所示：
第一列是一门考试的成绩，第二列就是另一门的成绩，最后一列就是是否录取。

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
...

1.数据的展示[可视化处理]
代码如下，和ch01大同小异：

def visualize_data():
    file_path = "./ex2data1.txt"
    data = pd.read_csv(file_path, names=["Exam1", "Exam2", "Admitted"])
    data = np.array(data)
    length = len(data)
    yellow_points_x = []
    yellow_points_y = []
    black_points_x = []
    black_points_y = []
    for i in range(length):
        if data[i, -1] == 0:
            yellow_points_x.append(data[i, 0])
            yellow_points_y.append(data[i, 1])
        else:
            black_points_x.append(data[i, 0])
            black_points_y.append(data[i, 1])
    plt.scatter(black_points_x, black_points_y, marker='+', color="black", label="Admitted")
    plt.scatter(yellow_points_x, yellow_points_y, marker='o', color="yellow", label="Not admitted")
    plt.legend(loc="best")
    plt.show()

我的思路是为黄点和黑点分别设置装取x坐标和y坐标的list。
然后遍历我们整个ndarray类型的data，将这些点按规则装取最后显示。
最后的结果如下：

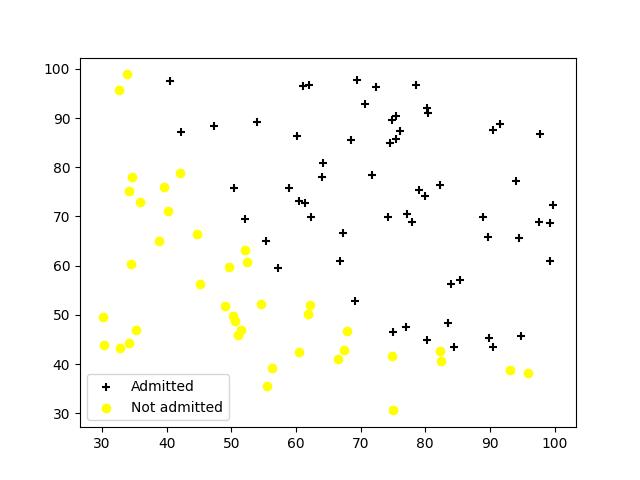
2.拟合出我们的决策边界，一条好的边界可以比较清晰且高准确率地划分图中的黄黑点。在执行这步之前我们肯定是需要先拟合出theta权值的。
赞一篇很清晰的逻辑回归损失函数求导过程[逻辑回归梯度下降法求导推演]。

我们这次同样用两种方法来做这题。
(1).梯度下降法。
可以看见我的iterations之大和learning_rate之小，确实很夸张，但学习率哪怕稍微再大一点好像就会过拟合，也不愿意花时间去调参数。这个设置可能会花费你8mins的样子抛出最后的损失值大致为0.253，和答案的0.203显然还有差距。

def logistic_regression():
    file_path = "./ex2data1.txt"
    data = pd.read_csv(file_path, names=["Exam1", "Exam2", "Admitted"])
    data = np.array(data)
    # now we have the corresponding X & Y data, apply gradient descent algorithm to the data
    X = data[:, :-1]
    Y = data[:, -1].reshape(-1, 1)
    # after extracting X & Y, assume theta as the coefficient and iterable reform it
    # add a column which is filled with 1 to the left of X
    length = len(X)
    beta = np.ones((length, 1))
    X = np.column_stack((beta, X))
    theta = np.zeros((3, 1))
    use_opt(theta, X, Y)
    
    iteraions = 9999999
    learning_rate = 0.0001
    for i in range(iteraions):
        temp_result = np.dot(X, theta)
        temp_result = 1 / (1 + np.exp(-temp_result))
        # xt = Y * np.log(temp_result)
        loss = np.sum(-Y * np.log(temp_result) - (1 - Y) * np.log(1 - temp_result)) / length
        print("loss is  %f" % loss)
        for j in range(3):
            X_j = X[:, j].reshape(-1, 1)
            temp = (temp_result - Y) * X_j
            derivative = np.sum((temp_result - Y) * X_j)
            theta[j, 0] = theta[j, 0] - learning_rate * derivative / length

(2).scipy库函数帮助我们来拟合。
其实对于这个库函数具体怎么设置参数以及其函数究竟该返回什么我不是很清楚，官方文档写得也有点难以捉摸。主要参考了这篇blog——scipy库optimize函数使用

其实各部分代码相信不困难，因为就是上面梯度下降法的一个分解过程而已。
但仔细看博客会发现其中作为Label的Y和作为拟合系数的theta都是以向量形式传入optimize函数使用的！
emmm，就是这个关键点罢了，我也是被折磨了好久，具体大神们怎么解决这个维度问题的得去看源代码，但简单来说就是内部机制会优化你这个bug。

代码：

def sigmoid(result):
    ans = 1 / (1 + np.exp(-result))
    return ans


def cost(theta, X, Y):
    temp_result = np.dot(X, theta)
    temp_result = sigmoid(temp_result)
    # xt = Y * np.log(temp_result)
    loss = -np.mean(np.multiply(Y, np.log(temp_result)) + np.multiply((1 - Y), np.log(1 - temp_result)))
    return loss


def grad(theta, X, Y):
    m = X.shape[0]
    loss = sigmoid(np.dot(X, theta)) - Y

    gradient = np.dot(X.T, loss) / m
    return gradient


def use_opt(w, X, Y):
    result = opt.minimize(fun=cost, x0=w, args=(X, Y), method='TNC', jac=grad)
    # temp = result
    print(result)
    # print("cost is %f" % cost(result[0], X, Y))


# 上面的函数做的就是把我们下面这个大的梯度下降法做一个分解
# 符合模块化思想的同时做到可以刚好利用fmin_tnc


def logistic_regression():
    file_path = "./ex2data1.txt"
    data = pd.read_csv(file_path, names=["Exam1", "Exam2", "Admitted"])
    data = np.array(data)
    # now we have the corresponding X & Y data, apply gradient descent algorithm to the data
    X = data[:, :-1]
    Y = data[:, -1]
    # after extracting X & Y, assume theta as the coefficient and iterable reform it
    # add a column which is filled with 1 to the left of X
    length = len(X)
    beta = np.ones((length, 1))
    X = np.column_stack((beta, X))
    theta = np.zeros(3)
    use_opt(theta, X, Y)

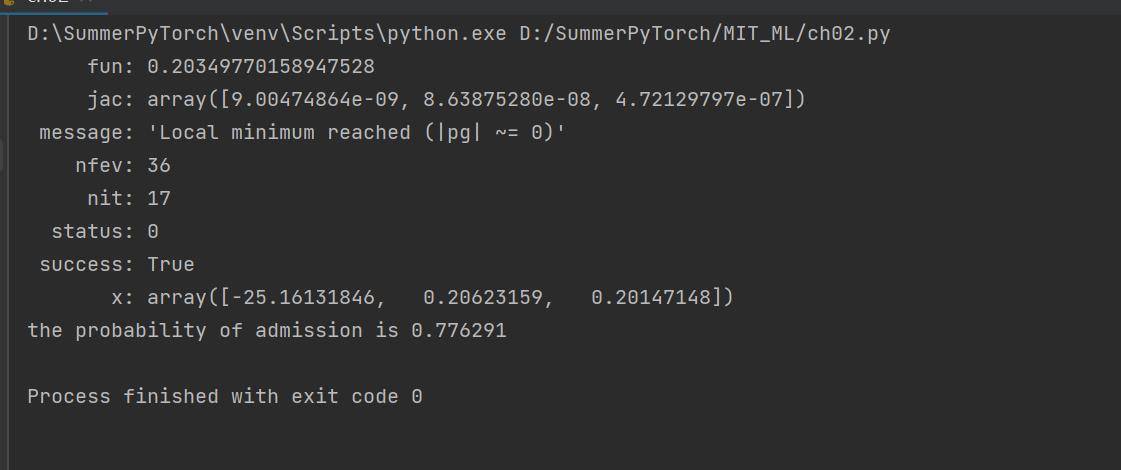
打印的result结果如下：这就与Andrew老师给出的答案一致了。

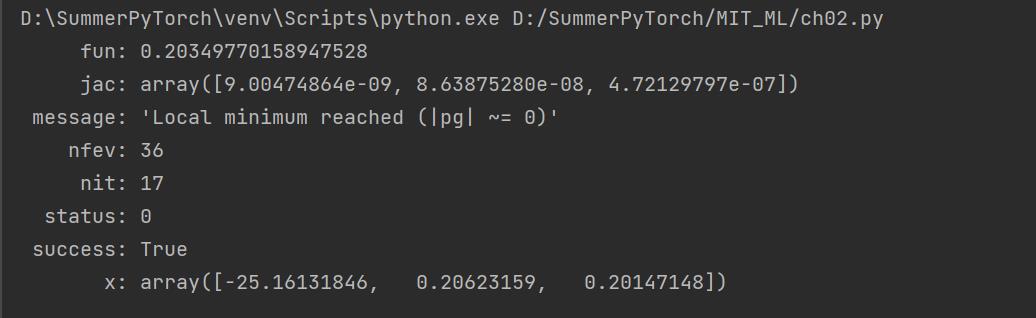
(3).预测[45， 85]的学生最后被录取的概率。
直接接上述，把拟合出来的theta进行调用即可，别忘了用sigmoid进行激活。
使用之前要debug一下我们的opt里的result变量，是一个optimizer类型的变量，其属性x就是我们需要的theta拟合系数！
所以我们修改use_opt代码如下：

def use_opt(w, X, Y):
    result = opt.minimize(fun=cost, x0=w, args=(X, Y), method='TNC', jac=grad)
    # temp = result
    print(result)
    # print("cost is %f" % cost(result[0], X, Y))

    temp_student = np.array([1, 45, 85])
    print("the probability of admission is %f" % sigmoid(np.dot(result.x, temp_student)))

最新结果如下图所示：可以看见录取率是符合Andrew在作业里给出的答案的。

(4).画出决策边界。
因为我们拟合出参数后应该是认为这条直线是
thata[0] + thata[1] * X[1] + theta[2] * X[2] = 0，然后sigmoid(0) = 0.5。
这样一来就好解释了，这条线刚好映射在概率为0.5的地方，其上下两部分刚好就是录取和非录取啦！
这是我自己想出来的解释，不知道合不合理。。。

以下代码就是通过计算出两个端点的值来连接成一条直线。

def plot_decision_bound(result, X):
    # print(X[:, 1].max(), X[:, 2].max())
    x_labels = [X[:, 1].min(), X[:, 1].max()]
    y_labels = [X[:, 1].min() * result.x[1] + result.x[0], X[:, 1].max() * result.x[1] + result.x[0]]/(-result.x[2])

    visualize_data()
    plt.plot(x_labels, y_labels, c='b', label="Boundary Line")
    plt.legend()
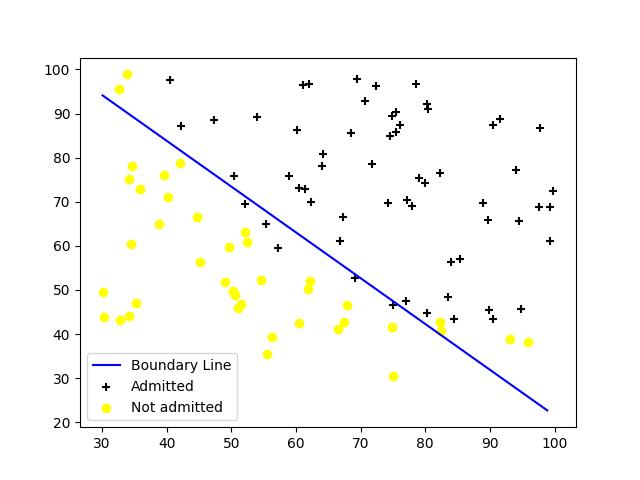
    plt.show()

得到的决策边界如下所示。

(5).data2的数据可视化，只要把文件名一改，把read_csv里的names一改就可以得到结果了，如下图所示：

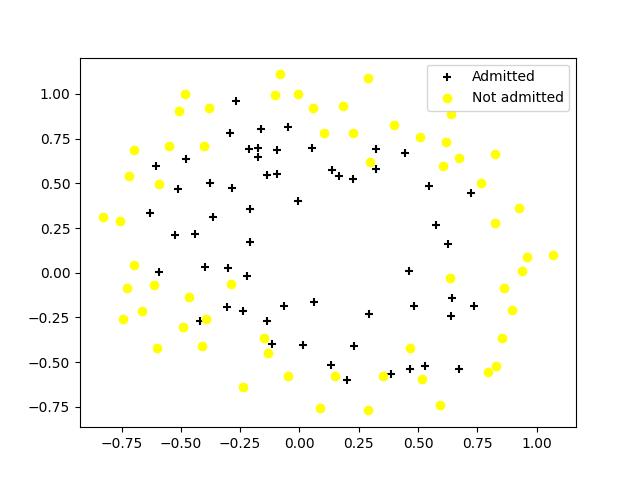
(6).特征映射，扩充特征的维度。这里有一个map_feature的函数如下：

def map_feature(X1, X2):
    """
    我们进行特征映射操作：思路是创建一个刚好的Factors然后每一轮循环进行相应地填充
    思路二:用hstack的方法，也就是我们常用的column_stack方法，将每一列进行堆叠也是可以的
    """
    length = len(X1)
    beta = np.ones(length)
    degree = 6
    num = int((2 + degree + 1) * degree / 2 + 1)
    Factors = np.zeros((length, num))
    Factors[:, 0] = beta
    ptr = 1
    for i in range(1, degree + 1):
        for j in range(0, i + 1):
            Factors[:, ptr] = np.power(X1, i - j) * np.power(X2, j)
            ptr += 1
    return Factors

degree就是我们需要的最高的维度，这里我们可以很轻松地识别出这个决策边界并不是线性的。所以我们把特征进行了补充补充为：
[X₁¹,X₂¹,X₁²,X₁¹X₂¹,X₂²… ,X₁⁶,…,X₂⁶]
所以可以看见我先计算出了一个num来表示扩充后的所有维度，然后控制两个循环将按上面的顺序逐个地放入预先建立好的Factors中！

(7).画等高图，我们刚刚说那个决策边界显然不是线性的。
于是这里我们实际上采用的是等高图！
这个时候可以发挥一下空间想象能力，想成在一个三维空间内，一组对应的[X，Y]有一个相应的Z，最后我们把Z = 0.5那一环映射下来即可，因为sigmoid之后0.5刚好是边界。
改装后的use_opt2函数如下，增加了画等高线图的步骤：

def use_opt_2(w, X, Y, lam):
    result = opt.minimize(fun=cost_high_index, args=(X, Y, lam), jac=grad_high_index, x0=w, method='TNC')
    # temp = result
    print(result)

    # 直接把决策边界集成在同一个函数内
    visualize_data()

    # 画等高线图
    u = np.linspace(-1, 1.5, 50)
    v = np.linspace(-1, 1.5, 50)

    z = np.zeros((len(u), len(v)))
    for i in range(len(u)):
        for j in range(len(v)):
            z[i, j] = sigmoid(np.dot(map_feature(u[i].reshape(-1, 1), v[j].reshape(-1, 1)), result.x))

    z = np.transpose(z)
    c = plt.contour(u, v, z, [0.5, 1.0])
    plt.clabel(c, inline=True, fontsize=10)
    plt.show()

大致步骤就是我们生成了两组数据u、v，这就相当于是x、y，至于这个范围是[-1, 1.5]可以看我们数据集2的图，大致就是这个范围，当然也可以调得更精细些。

z是一个二维的数组，也是用填充的方式来进行处理。
因为单独的u[i] or v[j]都是一个浮点数，而我们传入map_feature函数的需要是一个向量或者矩阵，这里我们将其变换成一个矩阵后再进行传入，会返回一个 1行28列 的扩维后的矩阵。
result.x是我们拟合出来的theta系数，就是一个向量(28,)。
两者做点乘得到的是一个数值，直接调用sigmoid之后存入。

至于transpose，是因为说是coutour函数规定X和Y必须得是反着来的！

contour参数就是X，Y，Z，最后那个就是一个把高度映射下来吧，如果某一个值我们设为0或者1.0那么那一条等高线并不会显示，这样说有点吃力，自己可以尝试以下几组:[0, 0.5], [0.3, 0.5], [0.5, 0.8], [0.5, 1.0]
大概就知道是个啥玩意儿了。
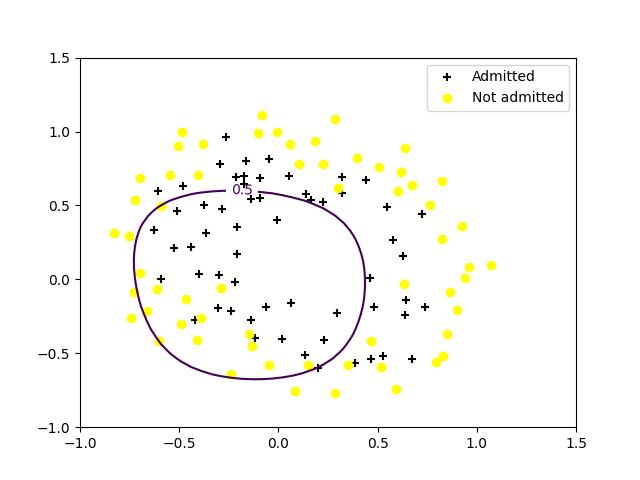
[0.5, 1.0]的结果

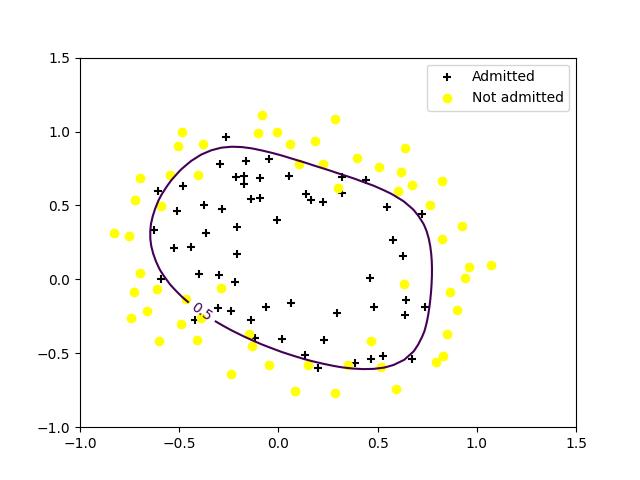
(8).调整学习率lamda的问题，就是做到欠拟合，过拟合。
这里就展示一个欠拟合的，把学习率调整大一些为100。
其他的改一个参数就行，应该不难。

总结

在逻辑回归问题下，对交叉熵损失函数的理解以及求导问题理解更加深刻。
这是最重要的，其次：
对如何去画出决策边界有了一定的了解。
对如何去调用scipy的自动优化函数也有了一定了解。