图像描述符（Image Descriptor）

Posted 2023-02-22 mini梁翊洲MAX

图像描述符的选取决定了我们如何量化图像，它的输出是特征向量，是图像本身的抽象。简单地说，它是用于表示图像的数字列表。

在现实图像处理的问题中，我们往往需要对图像进行一定的预处理从而将我们感兴趣的特征提取出来，从而大大减少计算量，增加精确度。

下面，我将用比较通俗的语言介绍和展示几种图像描述符的原理和处理结果。

颜色描述符

比较简单的应用有计算每个通道颜色的平均值和标准差，并利用它进行对比分析。

或者是利用颜色直方图（Color Histograms）。颜色直方图可以统计像素取值范围内像素的数量，从而完成对图片颜色整体的一个估计，我们尝试运行下代码看看。

我们要处理的图像是关于大海的，我们可以很清晰地看到明亮的蓝色占据了大部分的区域。为了直观感受，这里我们对查看每个通道的颜色直方图，但一般应用时我们会三个通道合并在一起。

导入必要的库和图像。

from matplotlib import pyplot as plt
import numpy as np
import argparse
import cv2

ap=argparse.ArgumentParser()
ap.add_argument("-i","--image",required=True)
args=vars(ap.parse_args())

image=cv2.imread(args["image"])

将图像按通道分割，我们这里注意到图像通道的排列顺序并不是我们口中常说的RGB，而是BGR。

chans=cv2.split(image)
colors=("b","g","r")

计算各通道的颜色直方图并展示出来。

这里calcHist()就是计算颜色直方图的函数。第一个参数一般是输入的图像，因为我们这里是一个通道一个通道计算，所以我们每次输入一个通道。第二个参数是询问计算输入的哪个通道，我们就只输入了一个通道，所以就计算第一个通道。第四个参数是bin，例如，我们将bin设为2，那么意味着我们将像素范围[0,255]等比例分为2份[0,127];[128,255]。第五个参数是像素的取值范围。

plt.figure()
plt.title("Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
features=[]

for (chan,color) in zip(chans,colors):
    hist=cv2.calcHist([chan],[0],None,[256],[0,256])
    features.extend(hist)

    plt.plot(hist,color=color)
    plt.xlim([0,256])
    
plt.show()

结果

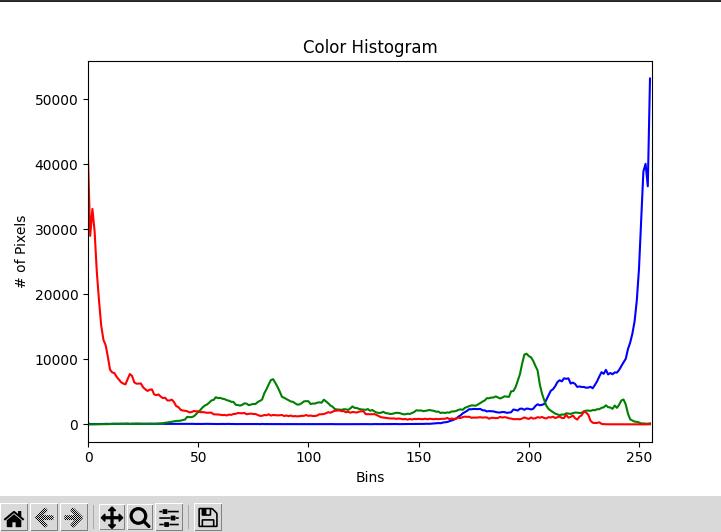
形状描述符

当使用形状描述符时，第一步通常是应用分割或边缘检测技术，使我们能够严格关注我们想要描述的形状的轮廓。然后，一旦我们有了轮廓，我们就可以再次计算统计矩来表示形状。

在这里，我们介绍Hu矩（Hu Moments），它被广泛用作简单的形状描述符。其数学原理对于数学一般的同学可能会比较复杂，我在此尽量用通俗的方法来解释。
对于一副M×N的数字图像，其p+q阶几何矩为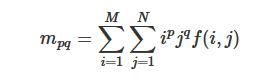：i和j表示某一像素点的坐标x和y。f(i,j)为图像在坐标点(i,j)处的灰度值。当p和q都为0时，是0阶几何矩，表示该图像像素值的总和，可看作是图像的灰度质量。当p或者q为1，另一个为0时，时1阶几何矩，可以表示x方向或者y方向像素值的求和，可以利用1阶几何矩除以0阶几何矩求得质心。

其中心矩为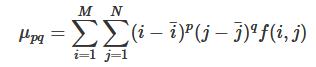：中心距实现了平移不变性。这是因为一个物体如果进行平移了的话，以任一原点为参考点的话，其所有坐标都发生了变化。但是如果我们以这个物体的某一点为参考，这个点随着整体一起移动，而整体的各个部位相对于这个参考点却是没变的。所以我们这里取质心为参考点，即分别减去质心的横坐标和纵坐标，就可以实现平移不变性。

进一步我们再引入规格化中心距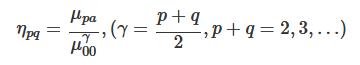：这个矩消除了图像比例变化带来的影响，即对象放大或者缩小也不会对这个矩的数值有太大的影响。原理其实也很简单，举个类似的例子方便大家理解。我们可以想象一个长方形，如果我们放大或者缩小它时，它的面积，边长都发生了变化。但是，它的长宽比却是始终不变的。

而Hu矩则利用上面的矩计算了7个数：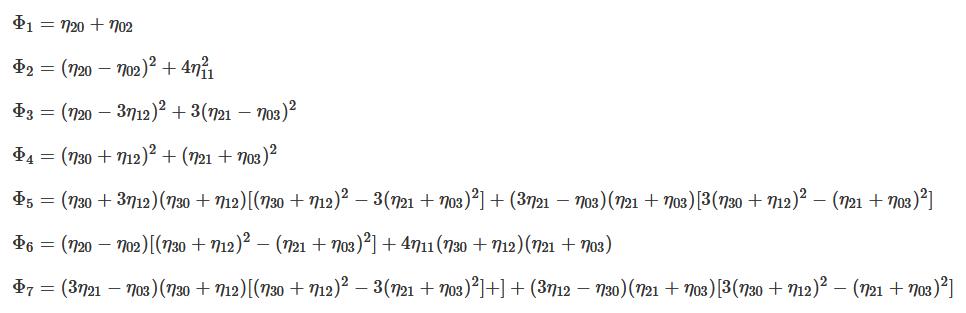

看到这么一大串后是不是感觉头疼？其实我们没必要去了解大佬是怎么得出来的这一堆东西，但是我从中观察出了一些有趣的现象。前面我们提到了平移不变性和缩放不变性，但是当我们对非堆成的图像进行上下（左右）翻转时，我们求的矩似乎会发生很大变化，但其形状却没有变化啊。那么我们如何得到翻转不变性呢？答案就在这一大串里面。

首先，我先把减弱翻转影响的原理说出来。我们刚刚说到，对于不对称的图形，翻转的影响尤其明显。我们举个例子，假设一个图形是[-9,1]，如果我们只是把两个值相加当作一个特征值的话是-9+1=-8 。当我们将它翻转变成[-1,9]，再求它的特征值就变成-1+9=8了。变化非常明显，那么我们可以考虑改变它特征值的选取规则。

我们再回头看看刚才这个例子，之所以出现那么大的误差是因为值变化了但符号没变，于是我们可以让他们符号相等。我们可以取绝对值，但这个在计算机里实现相对麻烦点。我们还可以取平方，不管符号如何，平方之后都是正数。这样子我们取平方和相加作为特征值的话，就几乎没有变化了。
知道这一点后，我们看看上面的七个式子。我们仔细观察可以发现对于p或者q任意一个为奇数的数值，一般会进行一次平方。或者两个p或者q任意一个为奇数的数值相乘，以抵消符号带来的影响。

接下来，我们实际应用Hu矩来计算一下下面哆啦A梦的形状描述符。

导入相应的库和图片。

import mahotas
from imutils.paths import list_images
import numpy as np
import argparse
import pickle
import imutils
import cv2

ap=argparse.ArgumentParser()
ap.add_argument("-i","--image",required=True)
args=vars(ap.parse_args())


image=cv2.imread(args["image"])
cv2.imshow("image",image)
cv2.waitKey(0)
gray=cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)
cv2.imshow("gray",gray)
cv2.waitKey(0)

我们需要将灰度图阈值化，方便寻找边缘。

thresh=cv2.bitwise_not(gray)
thresh[thresh>0]=255
cv2.imshow("thresh",thresh)
cv2.waitKey(0)
outline=np.zeros(image.shape,dtype="uint8")
cnts=cv2.findContours(thresh.copy(),cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
cnts=imutils.grab_contours(cnts)
cnts=sorted(cnts,key=cv2.contourArea,reverse=True)[0]
cv2.drawContours(outline,[cnts],-1,255,-1)
cv2.imshow("outline",outline)
cv2.waitKey(0)

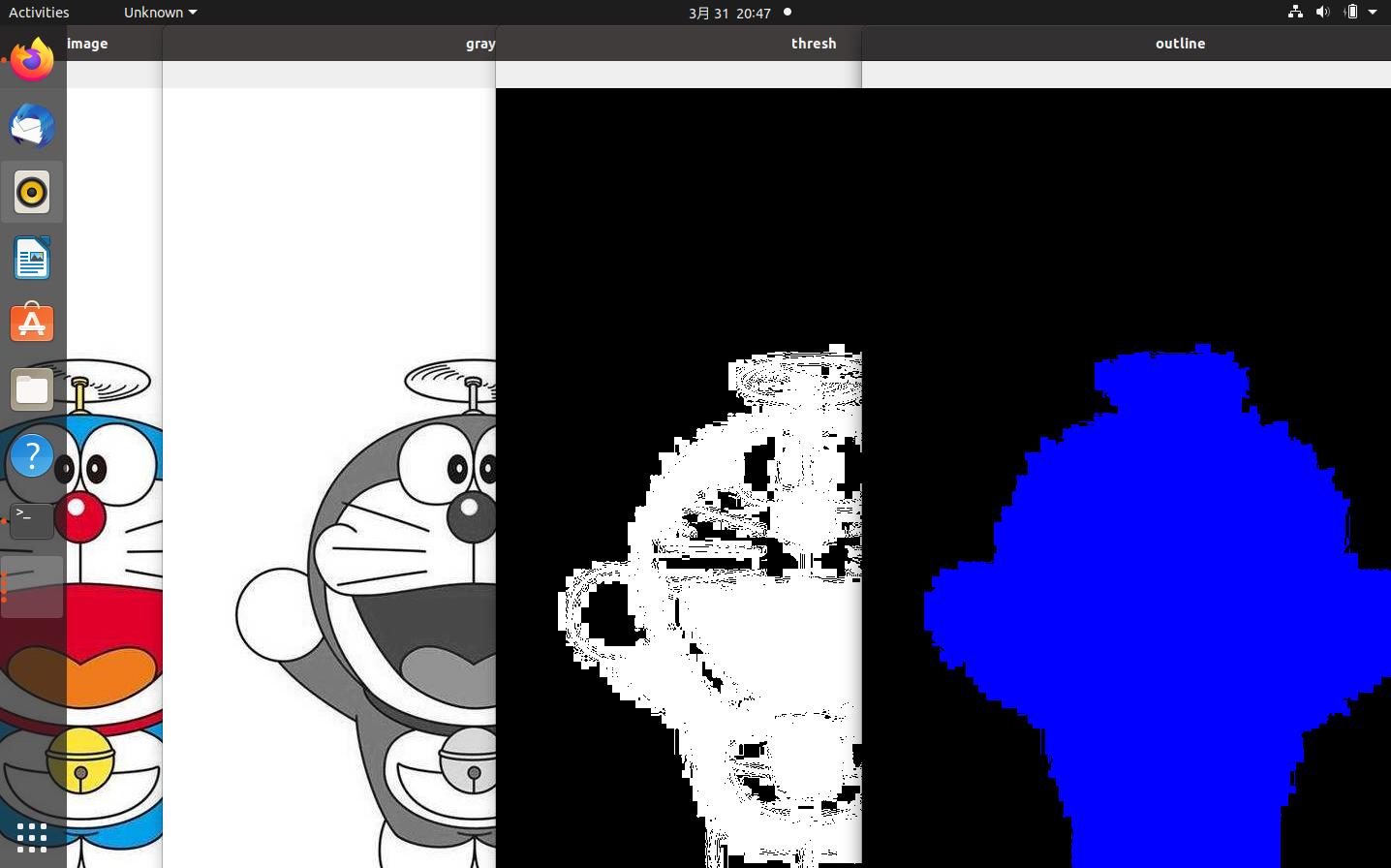
计算Hu矩

h_moments=cv2.HuMoments(cv2.moments(cnts)).flatten()
print(h_moments)

[1.74071461e-01 1.70471553e-03 6.92219552e-05 5.89352906e-06 1.13958626e-10 2.41123290e-07 3.44011832e-11]

在形状描述符开头我有提到过，在计算前我们需要对图像进行一些处理，这些处理在计算机视觉中经常需要用到。由于篇幅问题，我会在后续的博文中进行汇总介绍。

纹理描述符

提到纹理描述符，那就不得不说方向梯度直方图（ Histogram of Oriented Gradients），简称为hog。这个描述符在检测图像中的人物方面非常有用。

那么接下来我着重介绍这一个。

纹理描述符一般是对灰度图像进行操作。然后调整图像对比度，减少光照对图像的影响，使过曝或者欠曝的图像恢复正常。这种操作在图像处理方面很重要也很常见，但在这里我不打算展开来讲，以后会写相关文章的。HOG使用的是伽马矫正，有兴趣的可以去学习。

然后就是计算梯度了。在这里，我介绍下梯度是怎么算的。一般我们使用[-1 0 1]这样一个算子。假设我们对一块水平区域[-99 10 100]计算梯度，我们可以很清晰看到这块区域像素变化很大，即梯度很大。我们用算子和这片区域对应项相乘后-1 * -99+0 * 10+1 * 100=199，这就是梯度值。我们再看一块比较平滑的区域[20 25 23]，计算得到-1 * 20+0 * 25+ 1* 23=3，梯度值很小。当然，除了水平梯度还有垂直梯度。基于这两个梯度我们计算这块区域的合梯度（幅值和方向）。

得到了图像各个块梯度的幅值和方向后，我们根据orientations的数值，将方向（0-180）均等分成orientations段。然后根据方向的数值，将对应的幅值分配到各个段中，以得到特征描述符。这里我借用下图来让大家更清晰地看到这个过程。

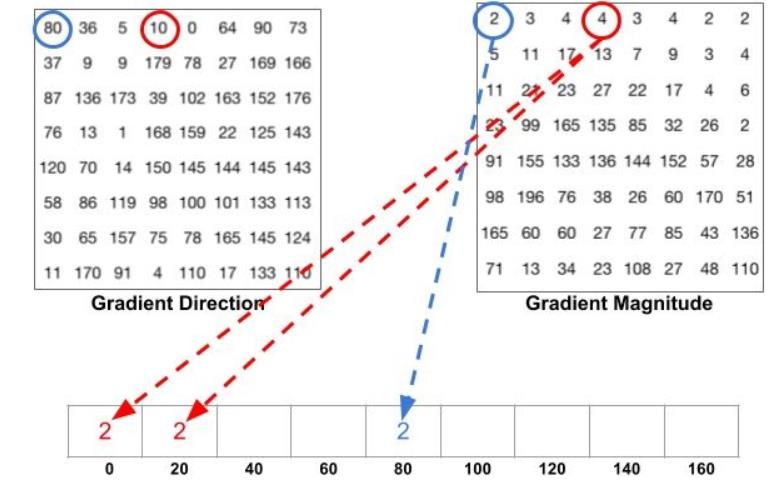后续我们通过归一化，滑动窗口来获取整幅图像的特征描述符，并将其可视化。

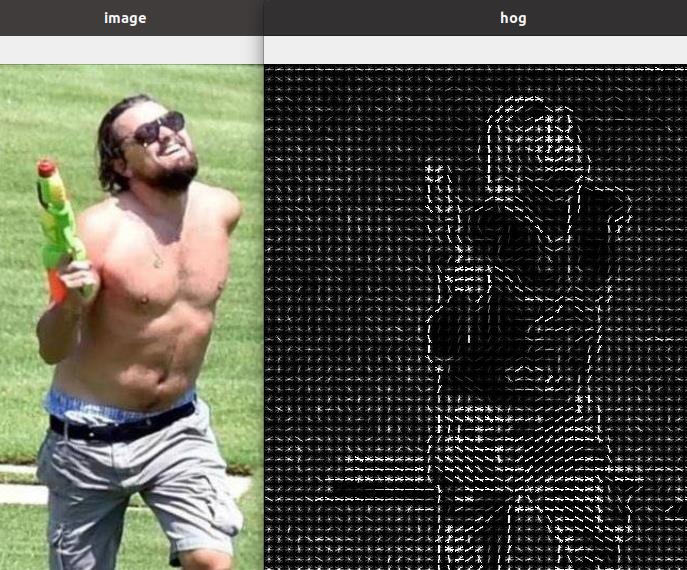
呼~说了那么一大堆，真正实操起来也不是简单的事。还好，在skimage里有相关的函数，操作起来就很方便了。我们就拿小李戏水的图片来实验下吧。

导入相应的库，图像并灰度化。

from skimage import feature,exposure
import cv2
import argparse

ap=argparse.ArgumentParser()
ap.add_argument("-i","--image",required=True)
args=vars(ap.parse_args())

image=cv2.imread(args["image"])
image=cv2.resize(image,(500,700))
gray=cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)

在hog（）函数里，除了gray和orientations我们知道了，还有其他几个参数。pixels_per_cell：一个cell里包含的像素个数，cell就是指我们计算梯度的一块小区域；cells_per_block：一个block包含的cell个数，滑动窗口一个个block地滑动；visualize：是否返回一个hog图像用于显示。

fd,hog_image=feature.hog(gray,orientations=9,pixels_per_cell=(10,10),cells_per_block=(2,2),visualize=True,channel_axis=None)
hog_image_rescaled=exposure.rescale_intensity(hog_image,in_range=(0,10))
cv2.imshow("image",image)
cv2.imshow("hog",hog_image_rescaled)
cv2.waitKey(0)

结果

“本站所有文章均为原创，欢迎转载，请注明文章出处：https://blog.csdn.net/kasami_/article/details/123853824。百度和各类采集站皆不可信，搜索请谨慎鉴别。技术类文章一般都有时效性，本人习惯不定期对自己的博文进行修正和更新，因此请访问出处以查看本文的最新版本。”