PostgreSQL中的B-TREE索引

Posted 2021-02-20 Warm water frog

• 分析了解pgsql中的索引
  • 前言
  • 索引
  • B-tree
    • B-Tree和B+Tree的区别:
    • pgsql中B-Tree
      • 实现
      • 如果该节点不是最右节点
      • 如果该节点是最右节点
  • 参考

分析了解pgsql中的索引

前言

pgsql中索引的支持类型好像还是蛮多的，一一来分析下

索引

PostgreSQL提供了多种索引类型： B-tree、Hash、GiST、SP-GiST 、GIN 和 BRIN。每一种索引类型使用了 一种不同的算法来适应不同类型的查询。

B-tree

首先我们需要弄明白一点b-tree就是btree。pgsql中使用的b-tree是btree的修改版本，引入了指向右兄弟节点的指针。

那么传统的btree和b+tree有什么区别呢？我们来探究下：

B-Tree和B+Tree的区别:

在B+Tree中，所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上，而非叶子节点上只存储key值信息，这样可以大大加大每个节点存储的key值数量，降低B+Tree的高度。

B-Tree：

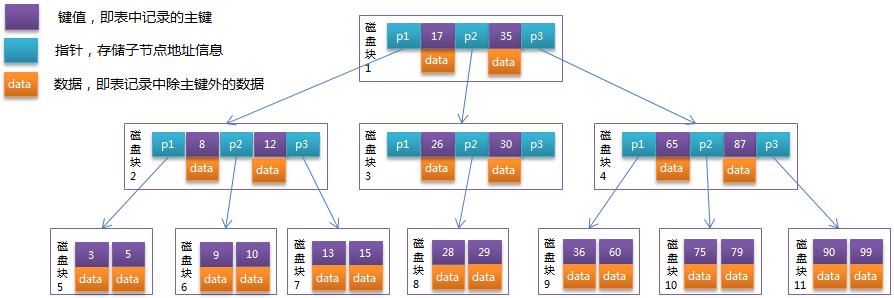
B+Tree:

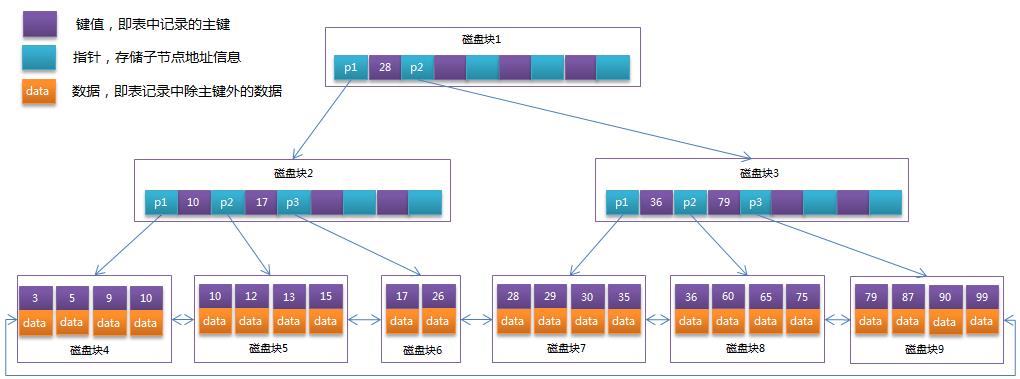
PostgreSQL的B-tree索引：

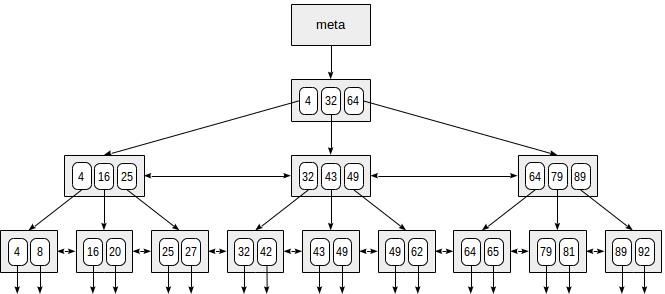
该索引最顶层的页是元数据页，该数据页存储索引root页的相关信息。内部节点位于root下面，叶子页位于最下面一层。向下的箭头表示由叶子节点指向表记录（TIDs）。 B-tree 中一个节点有多个分支，即每页（通常 8KB ）具有许多 TIDs 。

1、B-tree是平衡树，即每个叶子页到root页中间有相同个数的内部页。因此查询任何一个值的时间是相同的。

2、B-tree中一个节点有多个分支，即每页（通常8KB）具有许多TIDs。因此B-tree的高度比较低，通常4到5层就可以存储大量行记录。

3、索引中的数据以非递减的顺序存储（页之间以及页内都是这种顺序），同级的数据页由双向链表连接。因此不需要每次都返回root，通过遍历链表就可以获取一个有序的数据集。

b+tree会将行存储在索引页中，所以一页能存下的记录数会大大减少，从而导致b+tree的层级比单纯的b-tree深一些。 特别是行宽较宽的表。

例如行宽为几百字节，16K的页可能就只能存储十几条记录，一千万记录的表，索引深度达到7级，加上metapage，命中一条记录需要扫描8个数据块。

而使用PostgreSQL堆表+PK的方式，索引页通常能存几百条记录（以16K为例，约存储800条记录），索引深度为3时能支撑5亿记录，所以命中一条记录实际上只需要扫描5个块(meta+2 branch+leaf+heap)。

pgsql中B-Tree

B-tree可以在可排序数据上的处理等值和范围查询。
例如下面的集中场景:

<
<=
=
>=
>

实现

pgsql中B-tree的实现是根据《Effiicient Locking for Concurrent Operations on B-Trees》论文设计实现的。
Lehman和Yao的论文中，修改了B树的结构，不管是内部节点还是叶子节点，都有一个指针指向兄弟节点。同时还引入了“High Key”（下述HK）用于描述当前子节点的最大值。

其中的k1就代表一个HK,其值是p0以及p0子节点的最大值。HK并不作为索引结构中的一个元组，只是标记了一个最大的范围。同理，对于上述的2n个节点，每个节点都存在一个指针指向右兄弟节点，Pi的子节点取值范围为（Ki-1，Ki]。

然后来了解下：表和元组的组织方式
PostgreSQL的索引结构，也是按照这种方式进行存储的。

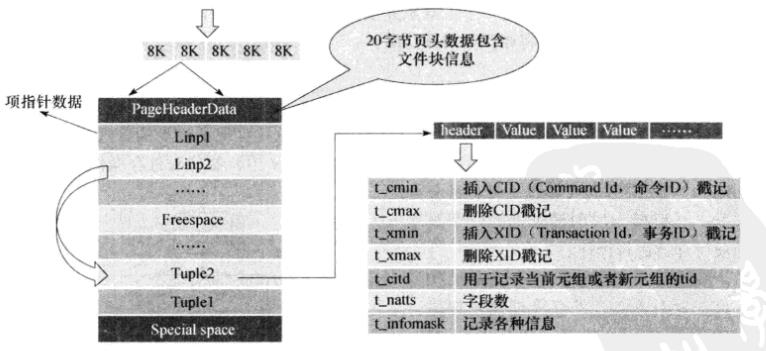
PageHeaderDate:是长度为20字节的页头数据，包括该文件块的一般信息，如：

• 空闲空间的起始和结束位置
• Special space的开始位置
• 项指针的开始位置
• 标志信息，如是否存在空闲项指针、是否所有的元组都可见

Freespase是指未分配的空间（空闲空间）

新插入的元组及其对应的Linp元素都会从Freespase空间来分配，Linp从Freespase头部开始分配，新元组（tuple）是从尾部开始分配。而PostgreSQL的索引结构，也是按照上述页面结构进行存储的。

Special space 是特殊空间：

用于存放与索引相关的特定函数。由于索引文件的文件块结构和普通的文件的相同，因此Special space在不同表文件块中并没有使用，
其内容被置为空。

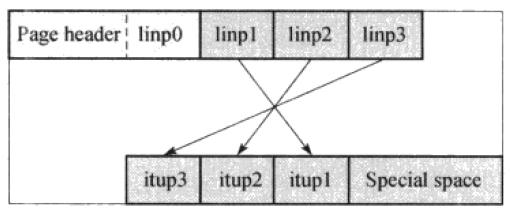
图中的itup是排好序的索引元组，itup1,itup2,itup3。它们是有序的。在page header后结构之后，是linp1,linp2它们存储的是元组在业内的实际位置，通过linp可以快速的访问到索引元组。

根据b-tree，每层的非最右节点需要一个最大关键值（High Key），通过它给出该节点索引关键字的范围。如果要插入的关键字大于High Key，就需要移动右边的节点，来寻找合适的插入点。

注意：linp0是page header中的内容，在这里只是为了描述方便将他拎出来了，在填充页面过程中，linp0是没有被赋值的，当页面填充完毕之后，根据情况进行不同的操作。也就是下文中当前节点，位置不同，进行的操作。

所以根据当前节点的位置有两种的调整方式：
1、在最右边
2、不在最右边

如果该节点不是最右节点

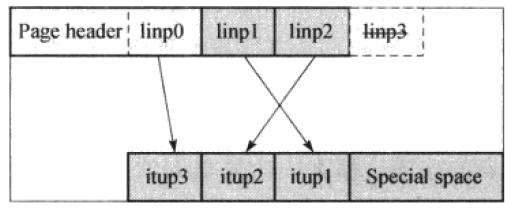
• 首先将itup3复制到该节点的右兄弟节点中，然后将linp0指向itup3（页面中的High Key）。
• 然后去掉linp3。也就是使用linp0指向页面的High Key。由于High Key（linp0）只是作为一个索引节点中键值的范围，并不指向实际的元组（itup3），所以去掉指向itup3的linp3。

如果该节点是最右节点

由于最有节点不需要High Key，所以linp0不需要保存High Key，将所有的linp递减一个位置，linp3同样不需要了。

每个节点都有一个指针指向右侧的兄弟，pgsql的实现使用了两个指针，分别指向左右的兄弟节点。这两个指针是由页面尾部的一块名为Special的特殊区域保存的，里面防止了一个由BTPageOpaqueData结构保存的数据。该数据结构记录了该节点在树结构中的左右兄弟节点的指针以及页面类型等信息。

/* Btree Page Operation queue Data Struct */
typedef struct BTPageOpaqueData
{
	BlockNumber btpo_prev;		/* 前一页块号，用于索引反向扫描　*/
	BlockNumber btpo_next;		/* 后一页快页快号，用于索引正向扫描 */
	union
	{
		uint32		level;		/* 页面在索引树中层次，0表示叶子层 */
		TransactionId xact;		/* 删除页面的是无用ID,永远判断该页面是否可以重新分配使用 */
	}			btpo;
	uint16		btpo_flags;		/* 页面类型 */
	BTCycleId	btpo_cycleid;	/* 页面对应的最新的Vacuum cycle ID */
} BTPageOpaqueData;

/* Bits defined in btpo_flags */
#define BTP_LEAF             (1 << 0)  /* 叶子页面，没有该标志标示非叶子页面 */
#define BTP_ROOT             (1 << 1)  /* 根页面（根页面没有父节点） */
#define BTP_DELETED          (1 << 2)  /* 页面已从树中删除 */
#define BTP_META             (1 << 3)  /* 元页面 */
#define BTP_HALF_DEAD        (1 << 4)  /* 空页面，单还保留在树中 */
#define BTP_SPLIT_END        (1 << 5)  /* 每一次页面分裂中，待分裂的最后一个页面 */
#define BTP_HAS_GARBAGE      (1 << 6)  /* 页面中含有LP_DEAD元组。当对索引页面中某些元组进行了删除后，该索引页面并没有立即从物理上删除这些元组，这些元组仍然保留在索引页面中，只是对这些元组进行了标记，同时索引页面中其他有效的元组保持不变 */

PostgreSQL所实现的BTree索引组织结构如下图：

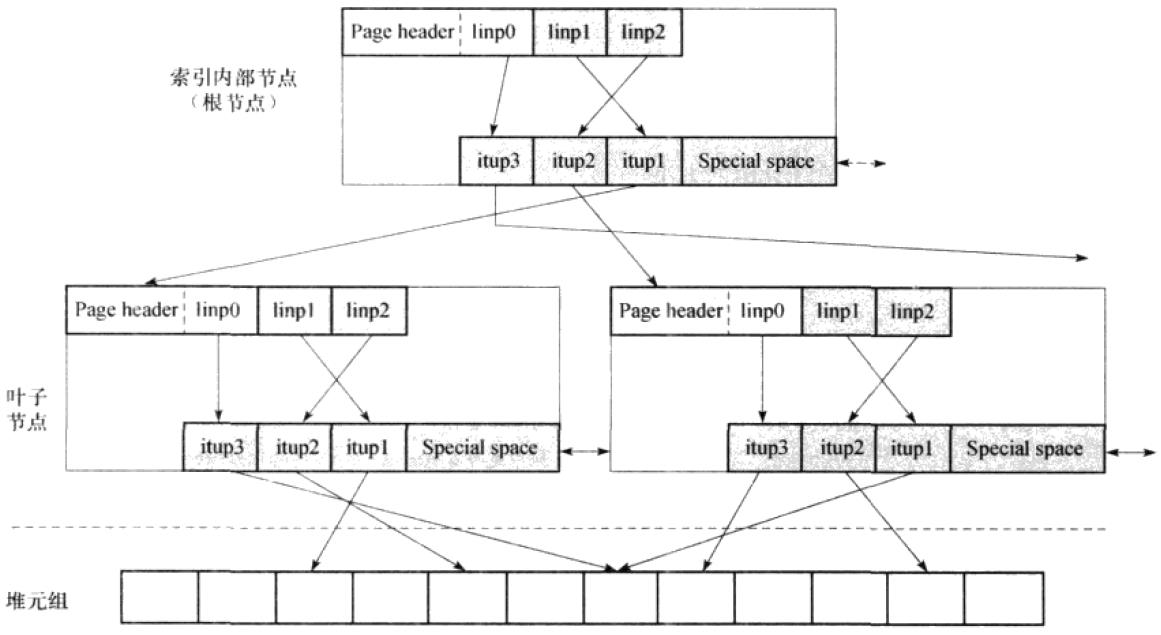
上图虚线上方的表示索引结构，虚线下方的为表元组。在叶子节点层，索引节点的指针指向表元组。每一个索引节点对应一个索引的页面，内部节点（包括根结点）与叶子节点的内部结构是一致的。
不同的是内部节点指向下一层的指针是指向索引节点的，而叶子节点指向的是物理存储的某个位置。

参考

【深入浅出PostgreSQL B-Tree索引结构】https://yq.aliyun.com/articles/53701
【PostgreSQL内核分析——BTree索引】https://www.cnblogs.com/scu-cjx/p/9960483.html
【B-Tree和B+Tree的区别】https://www.cnblogs.com/shengguorui/p/10695646.html
【PostgreSQL的B-tree索引】https://www.centos.bz/2019/06/postgresql的b-tree索引/
【为PostgreSQL讨说法 - 浅析《UBER ENGINEERING SWITCHED FROM POSTGRES TO mysql》】https://github.com/digoal/blog/blob/master/201607/20160728_01.md