二叉树详解及二叉树的前序中序后序遍历（递归和非递归）
Posted wanglelelihuanhuan
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二叉树详解及二叉树的前序中序后序遍历（递归和非递归）相关的知识，希望对你有一定的参考价值。
介绍二叉树之前先介绍一下树相关的概念。
树的定义：树是n（n>=0）个有限个数据的元素集合，形状像一颗倒过来的树。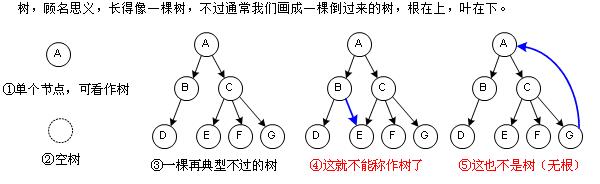
树的概念：
节点：结点包含数据和指向其它节点的指针。
根节点：树第一个结点称为根节点。
结点的度：结点拥有的子节点个数。
叶节点：没有子节点的节点(度为0)。
父子节点：一个节点father指向另一个节点child，则child为孩子节点，father为父亲节点
兄弟节点：具有相同父节点的节点互为兄弟节点。
节点的祖先：从根节点开始到该节点所经的所有节点都可以称为该节点的祖先。
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
树的高度：树中距离根节点最远节点的路径长度。
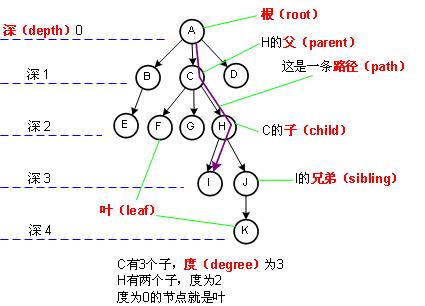
树的存储结构：
struct TreeNode
int _data;//节点值
TreeNode* _firstChild;//左孩子
TreeNode* _nextSlbling;//右兄弟
;树的应用：文件系统---目录树
介绍完树，接下来介绍二叉树。
二叉树定义：二叉树是一棵特殊的树，二叉树每个节点最多有两个孩子结点，分别称为左孩子和右孩子。
二叉树类型：
(1)完全二叉树——若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。 (2)满二叉树——高度为N的满二叉树有2^N - 1个节点的二叉树。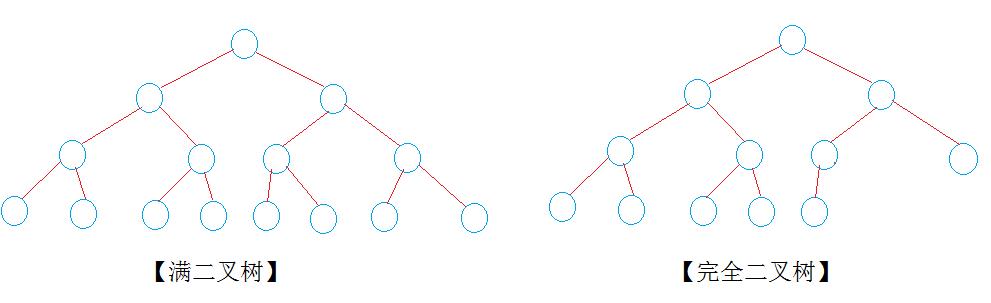
(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
二叉树的存储结构：
1、数组表示 ：用数组方式存储二叉树结构，就是用一组连续的存储单元存储二叉树的数据元素。数组存储法用于完全二叉树的存储表示非常有效，但是表示一般二叉树很不理想，容易造成空间浪费。此外，在一棵树中进行插入和删除时，需要多次移动节点，效率低。链式存储解决了这些缺点。
2、链式存储表示：二叉树的每一个节点至少包括三个域：数据data、左孩子节点指针leftChild、右孩子节点指针rightChild。这种链式结构称为二叉链表。为了便于查找任一节点的双亲节点，可以在节点中加一个双亲指针域parent，被称为三叉链表。
template <class T>
struct BinaryTreeNode
T _value;//节点值
BinaryTreeNode<T> *_left;//左孩子
BinaryTreeNode<T> *_right;//右孩子
BinaryTreeNode(const T& value)
:_value(value)
, _left(NULL)
, _right(NULL)
;
二叉树性质： (1) 在非空二叉树中，第 i 层的结点总数不超过
， i>=1；
(2) 深度为h的二叉树最多有
个结点(h>=1)，最少有h个结点；
(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；
(4) 具有n个结点的完全二叉树的深度为
；
(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
若I为结点编号则 如果I>1，则其父结点的编号为I/2；
如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；若2*I>N，则无左儿子；
如果2*I+1<=N，则其右儿子的结点编号为2*I+1；若2*I+1>N，则无右儿子。
(6)给定N个节点，能构成h(N)种不同的二叉树。 h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。
(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i。
二叉树遍历：
前序遍历(先根遍历):（1）先访问根节点； （2）前序访问左子树；（3）前序访问右子树；
1、递归前序遍历：（1）访问根节点（2）递归遍历左子树（3）递归遍历右子树
2、非递归前序遍历：通过栈实现。
如果根节点不为空，将根节点压入栈，访问根节点；如果根节点的左子树和右子树不为空，压根节点的右子树和左子树，访问根节点的左子树；如果左子树的左孩子不为空，压左孩子的右节点和左节点，访问左子树的左节点，如果为空，访问根节点的右树。
void PrevOrder_NonR() //前序遍历（非递归）
stack<BinaryTreeNode<T>* > s;
if (_root)
s.push(_root);
while (!s.empty())
BinaryTreeNode<T>* top = s.top();
cout << top->_value << " ";
s.pop();
if (top->_right)
s.push(top->_right);
if (top->_left)
s.push(top->_left);
cout << endl;
中序遍历: （1）中序访问左子树；（2）访问根节点； （3）中序访问右子树； 1、递归中序遍历：（1）递归遍历左子树（2）访问节点（3）递归遍历右子树 2、非递归中序遍历：通过栈实现。 如果根节点不为空，cur指向根节点，压所有左路节点，访问栈顶（最左节点），如果最左节点的右子树不为空，cur指向最左节点的右子树，如果最左节点的右子树不为空，压它的所有左路节点，如果最左节点的右子树为空，访问最左节点的根节点。
void InOrder_NonR() //中序遍历（非递归）
stack<BinaryTreeNode<T>* > s;
BinaryTreeNode<T>* cur = _root;
while (cur || !s.empty())
//左节点都入栈
while (cur)
s.push(cur);
cur = cur->_left;
if (!s.empty())
BinaryTreeNode<T>* top = s.top();
cout << top->_value << " ";
s.pop();
if (top->_right)
cur = top->_right;
cout << endl;
</span>后序遍历(后根遍历):（1）后序访问左子树；（2）后序访问右子树；（3）访问根节点； 1、递归后序遍历 （1）递归遍历左子树（2）递归遍历右子树 （3）访问节点 2、非递归后序遍历：通过栈实现。
void PostOrder_NonR() //后序遍历（非递归）
stack<BinaryTreeNode<T>* > s;
BinaryTreeNode<T>* cur = _root;
BinaryTreeNode<T>* vistedNode = NULL;
while (cur || !s.empty())
while (cur)
s.push(cur);
cur = cur->_left;
// 右为空或者右节点等于上一个访问的节点时，表示左右子树均已访问
BinaryTreeNode<T>* top = s.top();
if (top->_right == NULL || top->_right == vistedNode)
s.pop();
cout << top->_value << " ";
vistedNode = top;
else
cur = top->_right;
cout << endl;
void _LevelOrder(BinaryTreeNode<T>* root)
queue<BinaryTreeNode<T>* > q;
if (root)
q.push(root);
while (!q.empty())
BinaryTreeNode<T>* front = q.front();
cout << front->_value << " ";
q.pop();
if (front->_left)
q.push(front->_left);
if (front->_right)
q.push(front->_right);
完整代码：
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
template <class T>
struct BinaryTreeNode
T _value;//节点值
BinaryTreeNode<T> *_left;//左孩子
BinaryTreeNode<T> *_right;//右孩子
BinaryTreeNode(const T& value)
:_value(value)
, _left(NULL)
, _right(NULL)
;
template <class T>
class BinaryTree
public:
BinaryTree()
:_root(NULL)
BinaryTree(char *str)
_CreateTree(_root,str);
BinaryTree(BinaryTree<T>& t)
_root = _CopyTree(t._root);
/*BinaryTree& operator=(BinaryTree<T>& t)
if (this != &t)
_Destroy(t._root);
_CopyTree(t._root);
return *this;
*/
BinaryTree& operator=(BinaryTree<T> t)
swap(_root, t._root);
return *this;
~BinaryTree()
_DestoryTree(_root);
void _CreateTree(BinaryTreeNode<T>*& root,char*& str)
if (*str != '#'&&*str != '\\0')
root = new BinaryTreeNode<T>(*str);
_CreateTree(root->_left,++str);
if (*str == '\\0')
return;
_CreateTree(root->_right, ++str);
void PrevOrder_NonR() //前序遍历（非递归）
stack<BinaryTreeNode<T>* > s;
if (_root)
s.push(_root);
while (!s.empty())
BinaryTreeNode<T>* top = s.top();
cout << top->_value << " ";
s.pop();
if (top->_right)
s.push(top->_right);
if (top->_left)
s.push(top->_left);
cout << endl;
void InOrder_NonR() //中序遍历（非递归）
stack<BinaryTreeNode<T>* > s;
BinaryTreeNode<T>* cur = _root;
while (cur || !s.empty())
//左节点都入栈
while (cur)
s.push(cur);
cur = cur->_left;
if (!s.empty())
BinaryTreeNode<T>* top = s.top();
cout << top->_value << " ";
s.pop();
if (top->_right)
cur = top->_right;
cout << endl;
void PostOrder_NonR() //后序遍历（非递归）
stack<BinaryTreeNode<T>* > s;
BinaryTreeNode<T>* cur = _root;
BinaryTreeNode<T>* vistedNode = NULL;
while (cur || !s.empty())
while (cur)
s.push(cur);
cur = cur->_left;
// 右为空或者右节点等于上一个访问的节点时，表示左右子树均已访问
BinaryTreeNode<T>* top = s.top();
if (top->_right == NULL || top->_right == vistedNode)
s.pop();
cout << top->_value << " ";
vistedNode = top;
else
cur = top->_right;
cout << endl;
void Size()//节点个数
_Size(_root);
void LeafNodeNum()//叶子节点个数
_LeafNodeNum(_root);
void Depth() //深度
_Depth(_root);
void KLevelNodeNum()//第K层节点个数
_KLevelNodeNum(_root);
void PrevOrder()//递归前序
_PrevOrder(_root);
cout << endl;
void InOrder()//递归中序
_InOrder(_root);
cout << endl;
void PostOrder()//递归后序
_PostOrder(_root);
cout << endl;
void LevelOrder() //层序遍历
_LevelOrder(_root);
cout << endl;
protected:
void _DestoryTree(BinaryTreeNode<T>* root)
if (root)
_DestoryTree(root->_left);
_DestoryTree(root->_right);
delete root;
root = NULL;
BinaryTreeNode<T>* _CopyTree(BinaryTreeNode<T>* root)
BinaryTreeNode<T>* copyRoot = NULL;
if (root)
copyRoot = new BinaryTreeNode<T>(root->_value);
copyRoot->_left = _CopyTree(root->_left);
copyRoot->_right = _CopyTree(root->_right);
return copyRoot;
int _Size(BinaryTreeNode<T>* root)
if (root == NULL)
return 0;
if (root->_left == NULL&&root->_right == NULL)
return 1;
else
return 1 + _Size(root->left) + _Size(root->_right);
int _LeafNodeNum(BinaryTreeNode<T>* root)
if (root == NULL)
return 0;
else if (root->_left == NULL&&root->_right == NULL)
return 1;
else
int leftNum = _LeafNodeNum(root->_left);
int rightNum = _LeafNodeNum(root->_right);
return (leftNum + rightNum);
int _Depth(BinaryTreeNode<T>* root)
if (root == NULL)
return 0;
int leftDepth = _Depth(root->_left);
int rightDepth = _Depth(root->_right);
return 1 + (leftDepth > rightDepth ? leftDepth : rightDepth);
void _KLevelNodeNum(BinaryTreeNode<T>* root,int k)
if (root == NULL || k < 1)
return 0;
else if (k == 1)
return 1;
else
int leftNum = _LeafNodeNum(root->_left,k-1);// 左子树中k-1层的节点个数
int rightNum = _LeafNodeNum(root->_right,k-1);// 右子树中k-1层的节点个数
return (leftNum + rightNum);
void _PrevOrder(BinaryTreeNode<T>* root)
if (root)
cout << root->_value << " ";
if (root->_left)
_PrevOrder(root->_left);
if (root->_right)
_PrevOrder(root->_right);
void _InOrder(BinaryTreeNode<T>* root)
if (root)
if (root->_left)
_InOrder(root->_left);
cout << root->_value << " ";
if (root->_right)
_InOrder(root->_right);
void _PostOrder(BinaryTreeNode<T>* root)
if (root)
if (root->_left)
_PostOrder(root->_left);
if (root->_right)
_PostOrder(root->_right);
cout << root->_value << " ";
void _LevelOrder(BinaryTreeNode<T>* root)
queue<BinaryTreeNode<T>* > q;
if (root)
q.push(root);
while (!q.empty())
BinaryTreeNode<T>* front = q.front();
cout << front->_value << " ";
q.pop();
if (front->_left)
q.push(front->_left);
if (front->_right)
q.push(front->_right);
private:
BinaryTreeNode<T> *_root;
;
int main()
char* str = "12#3##45#6#7##8";
BinaryTree<char> bt1(str);
bt1.PrevOrder();
bt1.PrevOrder_NonR();
bt1.InOrder();
bt1.InOrder_NonR();
bt1.PostOrder();
bt1.PostOrder_NonR();
bt1.LevelOrder();
//cout<<"Size:"<<bt1.Size()<<endl;
//cout<<"Depth:"<<bt1.Depth()<<endl;
BinaryTree<char> bt2(bt1);
bt2.PrevOrder_NonR();
BinaryTree<char> bt3;
bt3 = bt1;
bt3.PrevOrder_NonR();
return 0;
以上是关于二叉树详解及二叉树的前序中序后序遍历（递归和非递归）的主要内容，如果未能解决你的问题，请参考以下文章