数据结构，如何根据邻接表画深度，广度优先生成树？

Posted 2023-05-16

1、如果节点的左右子树，则左链接字段lchild指示其左子节点（ltag = 0），否则，左链接字段指示其前身（ltag = 1）。如果节点具有右子树，则右链接字段rchild指示其右子节点（rtag = 0），否则，右链接字段指示其后继子（rtag = 1）。

2、单击以实现此过程，将指针p设置为指向当前节点，而pre始终指向刚访问的节点，即p的前任，以修改pre和前任的后继线索。 p的线索访问当前节点p以进行线程算法处理。

3、节点p的左指针字段为空，然后将标志位置设置为1，并且p-> lchild指向中间顺序的前任节点pre（即，左线程）； 

pre节点的右指针字段如果为空，则将其标志位置设置为1，并使pre-> rchild指向中间顺序的后继节点p（即右线程）；将pre指向刚访问的节点p（即pre = p），线程化p的右子树。

扩展资料：

令G =（V，E）为图，其中V = v1，v2，...，vn。 G的邻接矩阵是具有以下属性的n阶方阵：

对于无向图，邻接矩阵必须对称，并且主对角线必须为零（此处仅讨论无向简单图），对角线对角不一定为0，有向图也不一定如此。

在无向图中，任何顶点的度i是第i列（或第i行）中所有非零元素的数量，有向图中顶点i的出度是第i行中的所有非零元素。in-degree是第i列中的所有非零元素的数目。

参考技术A

深搜中枚举时由大到小就是这个结果。

#include"stdio.h"

#include"stdlib.h"

#define MaxVertexNum 100 //定义最大顶点数

typedef struct

char vexs[MaxVertexNum]; //顶点表

int edges[MaxVertexNum][MaxVertexNum]; //邻接矩阵，可看作边表

int n,e; //图中的顶点数n和边数e

MGraph; //用邻接矩阵表示的图的类型

//=========建立邻接矩阵=======

void CreatMGraph(MGraph *G)

int i,j,k;

char a;

printf("Input VertexNum(n) and EdgesNum(e): ");

scanf("%d,%d",&G->n,&G->e); //输入顶点数和边数

scanf("%c",&a);

printf("Input Vertex string:");

G->vexs[i]=a; //读入顶点信息，建立顶点表

for(i=0;i<G->n;i++)

for(j=0;j<G->n;j++)

G->edges[i][j]=0; //初始化邻接矩阵

printf("Input edges,Creat Adjacency Matrix\\n");

for(k=0;k<G->e;k++) //读入e条边，建立邻接矩阵

scanf("%d%d",&i,&j); //输入边（Vi，Vj）的顶点序号

G->edges[i][j]=1;

G->edges[j][i]=1; //若为无向图，矩阵为对称矩阵；若建立有向图，去掉该条语句

//=========定义标志向量，为全局变量=======

typedef enumFALSE,TRUE Boolean;

Boolean visited[MaxVertexNum];

//========DFS：深度优先遍历的递归算法======

void DFSM(MGraph *G,int i)

visited[i]=TRUE; //置已访问标志

for(j=0;j<G->n;j++) //依次搜索Vi的邻接点

if(G->edges[i][j]==1 && ! visited[j])

DFSM(G,j); //（Vi，Vj）∈E，且Vj未访问过，故Vj为新出发点

void DFS(MGraph *G)

int i;

for(i=0;i<G->n;i++)

visited[i]=FALSE; //标志向量初始化

for(i=0;i<G->n;i++)

if(!visited[i]) //Vi未访问过

DFSM(G,i); //以Vi为源点开始DFS搜索

//==========main=====

void main()

//int i;

MGraph *G;

G=(MGraph *)malloc(sizeof(MGraph)); //为图G申请内存空间

CreatMGraph(G); //建立邻接矩阵

printf("Print Graph DFS: ");

DFS(G); //深度优先遍历

printf("\\n");

扩展资料：

图的邻接表存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。

如词条概念图所示，表结点存放的是邻接顶点在数组中的索引。对于无向图来说，使用邻接表进行存储也会出现数据冗余，表头结点A所指链表中存在一个指向C的表结点的同时，表头结点C所指链表也会存在一个指向A的表结点。

参考资料来源：百度百科-邻接表

参考技术B

画出图，然后根据深度优先或者广度优先搜索遍历边，连接边，如果顶点访问过了，那就不连接边的两个顶点，我以深度优先为例，演示一下。

参考技术C 深搜中枚举时由大到小就是这个结果

数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）

目录

• 一、图的遍历概念
• 二、深度优先搜索（DFS）
• • （一）DFS算法步骤
  • • 1、邻接表DFS算法步骤
    • 2、邻接矩阵DFS算法步骤
  • （二）深度优先生成树、森林
  • （三）DFS的空间复杂度和时间复杂度
• 三、广度优先搜索（BFS）
• • （一）BFS算法步骤
  • • 1、邻接表BFS算法步骤
    • 2、邻接矩阵BFS算法步骤
  • （二）广度优先生成树、森林
  • （三）BFS的空间复杂度和时间复杂度
• 四、DFS和BFS的应用

一、图的遍历概念

图的遍历指从图中某一顶点出发（任意一个顶点都可以作为访问的起始顶点），按照某种遍历方法，对图中所有的顶点访问一次且只访问一次。图与树不一样，其中一个顶点可能与多个顶点相连，所以需记录已访问过的顶点，当访问一个顶点后，考虑如何选取下一个要访问的顶点。

• 图的遍历分为两种，深度优先搜索和广度优先搜索，这两种方法对无向图和有向图都适用。

二、深度优先搜索（DFS）

（一）DFS算法步骤

前面文章中，讲到过二叉树的先序遍历，其实这里图的深度优先搜索（DFS）是由其推广而来的。

二叉树的先序遍历中，首先是根结点，遍历完根结点的左子树，然后再遍历完根结点的右子树，依次下去至所有结点都遍历到。

• 图的深度优先搜索首先选取图中某一顶点v_i，访问后，任意选取一个与v_i邻接的顶点，且该顶点未被访问，……，继续重复该过程，直到图中所有与v_i连通的顶点都被访问到；若还有顶点未被访问到，则另外选取一个未被访问的顶点再次作为起始点，重复以上步骤，继续直至图中所有结点被访问。

可以看出DFS算法是一个递归过程，其中需借助一个栈完成操作。

写出下面这个图的深度优先遍历序列：

其深度优先遍历序列为：0，4，6，9，8，7，5，3，2，1。

1、邻接表DFS算法步骤

例如下面这个无向图：

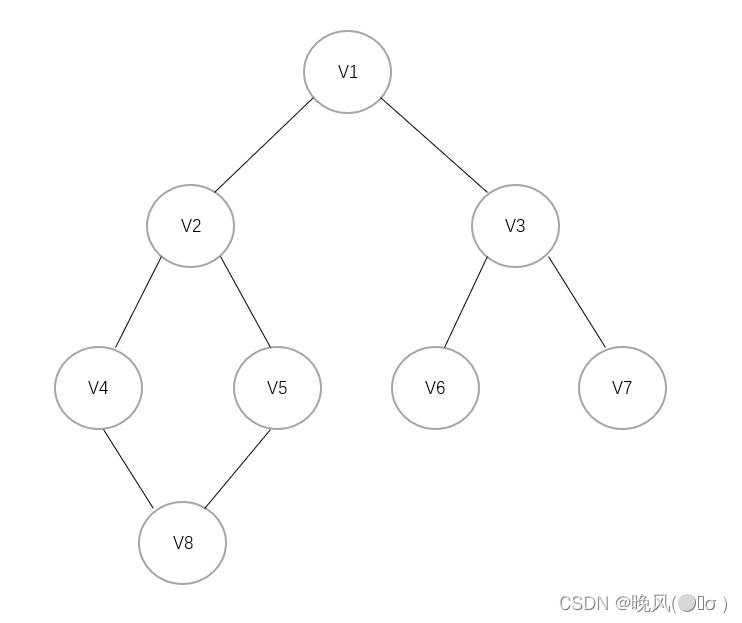
该图的邻接表如下：

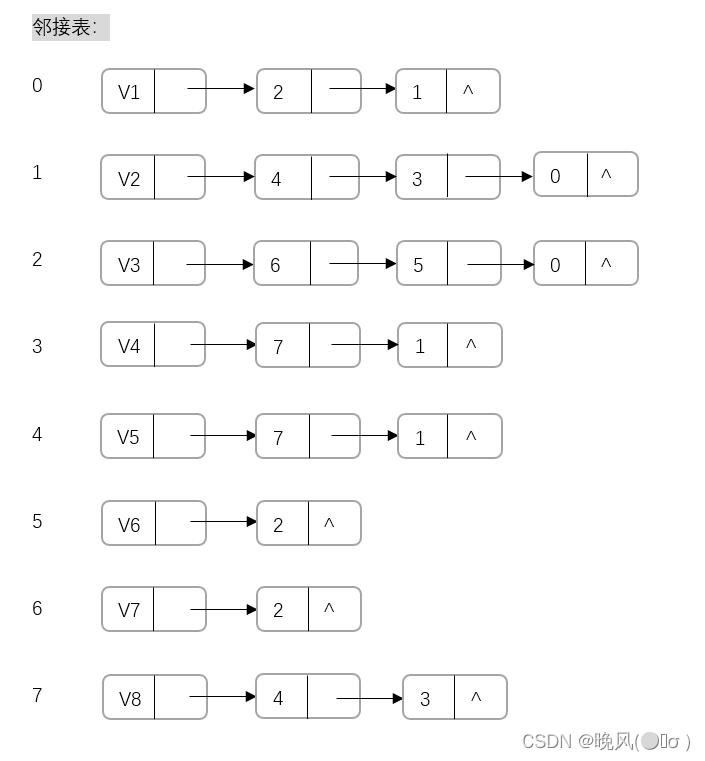
通过邻接表进行深度优先搜索的步骤如下（以V1为访问起始点，不唯一）：
1、首先访问0，即V1，访问后标记已访问过；
2、查看V1单链表，第一个未访问的邻接顶点为2，即V3，并以V3为出发点继续深度遍历；
3、查看V3单链表，其第一个未访问的邻接顶点为6，即V7，再以V7为出发点继续深度遍历；
4、查看V7单链表，其邻接顶点为2，即V3，它已经被访问过，于是回到V3单链表，搜索下一个未被访问的邻接顶点；
5、查看V3单链表，其下一个未访问的邻接顶点为5，即V6，以V6为出发点继续深度遍历；
6、查看V6单链表，其邻接顶点为2，也是已经被访问过，于是回到V3单链表，搜索下一个未被访问的邻接顶点；
7、查看V3单链表，其邻接顶点为0，即V1，一开始被访问过，于是回到V1单链表，搜索下一个未被访问的邻接顶点；
8、查看V1单链表，其下一个未访问的邻接顶点为1，即V2，并以V2为出发点继续深度遍历；
9、查看V2单链表，其第一个未访问的邻接顶点为4，即V5，再以V5为出发点继续深度遍历；
10、查看V5单链表，其第一个未访问的邻接顶点为7，即V8，再以V8为出发点继续深度遍历；
11、查看V8单链表，其邻接顶点为4，即V5，已经被访问过，于是回到V5单链表，搜索下一个未被访问的邻接顶点；
12、查看V5单链表，其下一个未被访问的邻接顶点为1，即V2，于是回到V2单链表，搜索下一个未被访问的邻接顶点；
13、查看V2单链表，其邻接顶点为3，即V4，并以V4为出发点继续深度遍历；；
14、查看V4单链表，其邻接顶点为7，即V8，再以V8为出发点继续深度遍历；
15、查看V8单链表，其邻接顶点为3，即V4，再以V4为出发点继续深度遍历；
16、查看V4单链表，其邻接顶点为1，即V2，再以V2为出发点继续深度遍历；
17、查看V2单链表，其邻接顶点为0，即V1，再以V1为出发点继续深度遍历；
18、查看V1单链表，其邻接顶点为2，即V3，V3中已经不存在未访问的顶点，于是回到V1单链表。
19、查看V1单链表，下一个邻接顶点为1，即V2，V2中已经不存在未访问的顶点，最后回到V1单链表，遍历完成。
故该图的深度优先遍历序列为：V1、V3、V7、V6、V2、V5、V8、V4。

2、邻接矩阵DFS算法步骤

通过图的邻接矩阵实现深度优先搜索，例如下面这个图（以V1为访问起始点，是唯一的）：

例如，对于下面这个有向图，对其进行深度优先搜索：

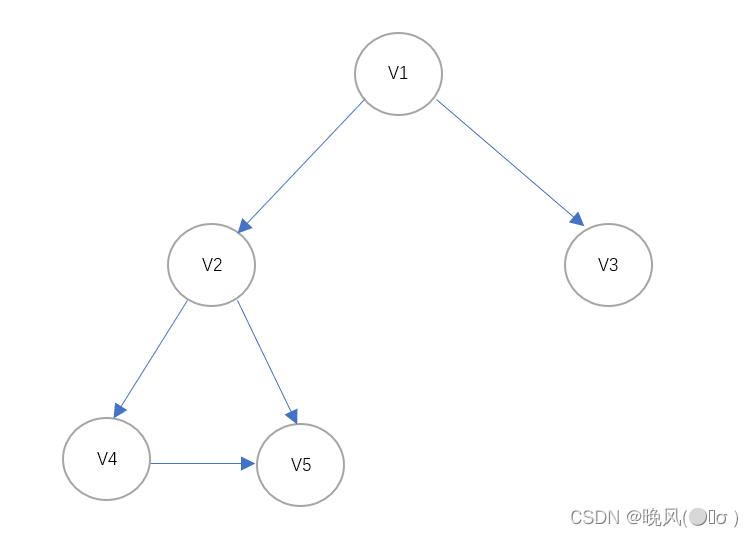
其邻接矩阵如下：

1、由V1开始，如下表【第一行为回退点，第二行为深度优先搜索得到的序列】：

V1

2、通过其邻接矩阵知，访问第一行第二列的1对应的V2顶点，由于它是在V1的行中被访问到的，所以回退点为V1：

	V1
V1	V2

3、由于访问了V2，即开始访问V2行，访问第二行第三列的1对应的V4顶点，由于它是在V2的行中被访问到的，所以回退点为V2：

	V1	V2
V1	V2	V4

4、由于访问了V4，即开始访问V4行，访问第四行第五列的1对应的V5顶点，由于它是在V4的行中被访问到的，所以回退点为V4：

	V1	V2	V4
V1	V2	V4	V5

5、由于访问了V5，即开始访问V5行，由于第五行都为0，回退到V4，由于V4行顶点都访问完，回退到V2，由于V2行顶点都访问完，回退到V1行，此时V1行还剩第一行第三列的1对应的V3顶点未访问，访问该顶点：

	V1	V2	V4
V1	V2	V4	V5	V3

6、至此，访问完了图中的所有顶点，即深度优先搜索序列为V1、V2、V4、V5、V3。

• ✨对于深度优先搜索（DFS），由于基于邻接表的遍历得到的序列可能不是唯一的，即根据边的输入次序不同，从而得到的邻接表不同，从而遍历序列不一样；而基于邻接矩阵所得到的DFS遍历序列是唯一的。

（二）深度优先生成树、森林

• 对一个连通图或非连通图进行DFS遍历后，若将在遍历过程中所经历过的顶点保留，则可以形成一棵树或森林，即深度优先生成树或深度优先生成森林；另外，基于邻接表存储的深度优先生成树或深度优先生成森林也是不唯一的；而对于邻接矩阵则是唯一的。

例如，上面这个无向连通图遍历DFS遍历生成的深度优先生成树如下（基于邻接表）：

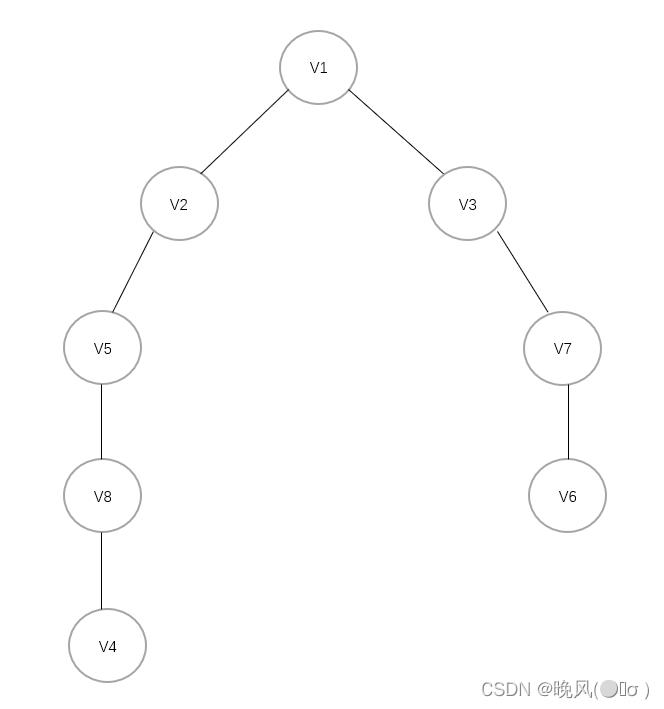
例如，对于上面这个有向图进行DFS遍历：

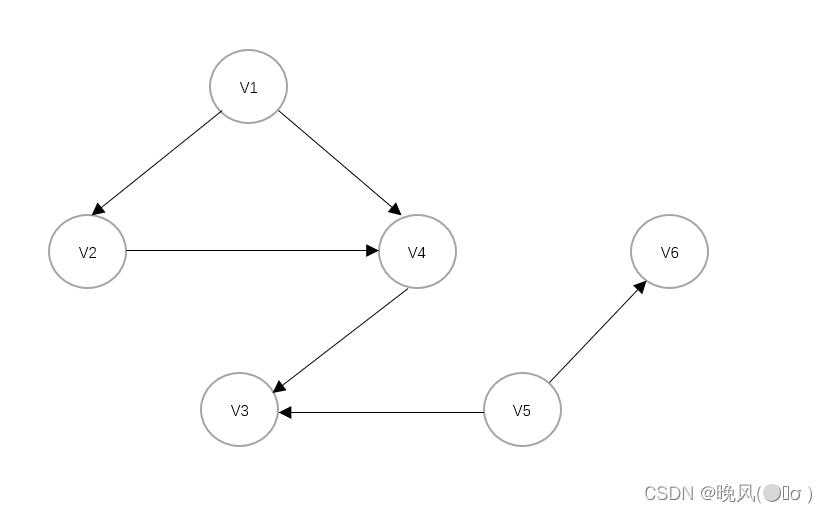
它并不是连通图，得到的深度优先生成森林如下：

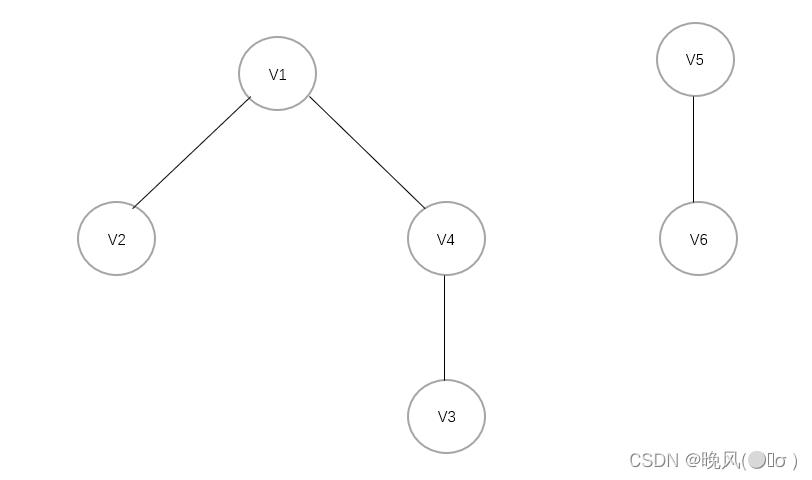
（三）DFS的空间复杂度和时间复杂度

对于一个图G=（V，E），由顶点集V和边集E组成。
1、DFS算法的空间复杂度

• ✨由于DFS算法是一个递归算法，即递归顶点集V，通过DFS遍历的空间复杂度为O(|V|)。

2、DFS算法的时间复杂度

• ✨时间复杂度取决于图的存储结构，若通过邻接矩阵表示图，则查找顶点的邻接顶点所需时间为O(|V|)，总时间复杂度为O(|V²|)（邻接矩阵为方阵n×n）；若通过邻接表表示图，则查找所有顶点的邻接顶点所需时间为O(|E|)，访问顶点所需时间为O(|V|)，即总时间复杂度为O(|V|+|E|)。

三、广度优先搜索（BFS）

（一）BFS算法步骤

前面文章中，讲到过二叉树的层序遍历，其实这里图的广度优先搜索（BFS）是由其推广而来的。

二叉树的层序遍历中，层次优先，当对一层的结点都遍历完后，遍历下一层，按照次序对每个结点的左、右孩子进行遍历。

• 图的广度优先搜索中需要借助到队列来遍历，首先选取一个起始点顶点v_i，访问后将其入队并标记为已访问（使用队列用于避免重复访问，存放已经访问过的各邻接顶点）；当队列不为空时检查出队顶点的所有邻接顶点，访问未被访问的邻接顶点并将其入队，……，继续重复该过程，直到图中所有与v_i连通的顶点都被访问到；当队列为空时跳出循环，则此时遍历完成。

可以知道BFS算法并不是递归过程，且要用到队列。

1、邻接表BFS算法步骤

例如下面这个无向图：

该图的邻接表如下：

通过邻接表进行广度优先搜索的步骤如下（这里以V1为访问起始点，不唯一）：
1、首先访问0，即V1，访问后标记已访问过，使其入队，然后删除当前队头结点；【V1】
2、遍历V1单链表，使其未访问的邻接顶点2、1入队并标记；【V2、V3】
3、访问队头结点1并删除，然后遍历1对应的V2单链表，使其未访问的邻接顶点4、3入队并标记；【V3、V4、V5】
4、访问队头结点2并删除，然后遍历2对应的V3单链表，使其未访问的邻接顶点6、5入队并标记；【V4、V5、V6、V7】
5、访问队头结点3并删除，然后遍历3对应的V4单链表，使其未访问的邻接顶点7入队并标记；【V5、V6、V7、V8】
6、访问队头结点4并删除，然后遍历4对应的V5单链表，该单链表中无未访问的顶点；【V6、V7、V8】
7、访问队头结点5并删除，然后遍历5对应的V6单链表，该单链表中无未访问的顶点；【V7、V8】
8、访问队头结点6并删除，然后遍历6对应的V7单链表，该单链表中无未访问的顶点；【V8】
9、访问队头结点7并删除，然后遍历7对应的V8单链表，该单链表中无未访问的顶点，此时队列为空，遍历结束；【】
故该图的深度优先遍历序列为：V1、V2、V3、V4、V5、V6、V7、V8。

2、邻接矩阵BFS算法步骤

通过图的邻接矩阵实现广度优先搜索，例如下面这个图（以V1为访问起始点，是唯一的）：

例如，对于下面这个有向图，对其进行广度优先搜索：

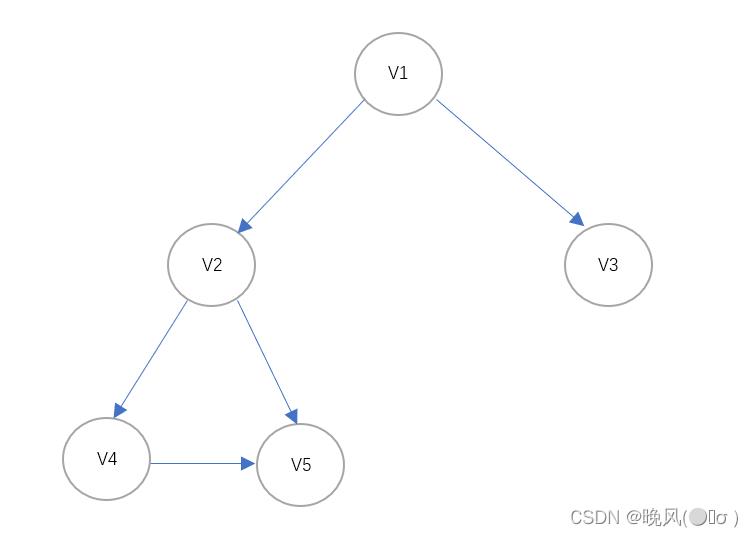
其邻接矩阵如下：

1、由V1行开始，如下表：

V1

2、可得与其匹配的有V2、V3，填到表中V1之后：

V1	V2	V3

3、由V2行开始，其中V4未访问，填到V3之后：

V1	V2	V3	V4

4、由V3行开始，都为0，继续下一行。
5、由V4行开始，其中V5未访问，填到V4之后：

V1	V2	V3	V4	V5

6、至此，该图的所有顶点都已访问到，得到的序列便是广度优先搜索，即深度优先搜索序列为V1、V2、V3、V4、V5。

• ✨同样，对于广度优先搜索，由于基于邻接表的遍历得到的序列可能不是唯一的，即根据边的输入次序不同，从而得到的邻接表不同，从而遍历序列不一样；而基于邻接矩阵所得到的遍历序列是唯一的，这两点和深度优先搜索遍历是一样的。

（二）广度优先生成树、森林

• 与DFS遍历一样， 对一个连通图或非连通图进行BFS遍历后，若将在遍历过程中所经历过的顶点保留，则可以形成一棵树或森林，即广度优先生成树或广度优先生成森林；另外，基于邻接表存储的广度优先生成树或广度优先生成森林也是不唯一的；而对于邻接矩阵则是唯一的。

例如，上面这个无向连通图遍历BFS遍历生成的深度优先生成树如下（基于邻接表）：

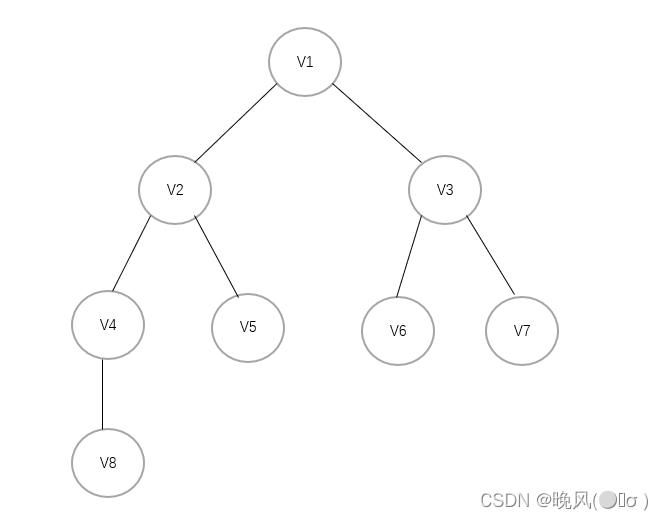
例如，对于上面这个有向图进行BFS遍历：

它并不是连通图，得到的广度优先生成森林如下：

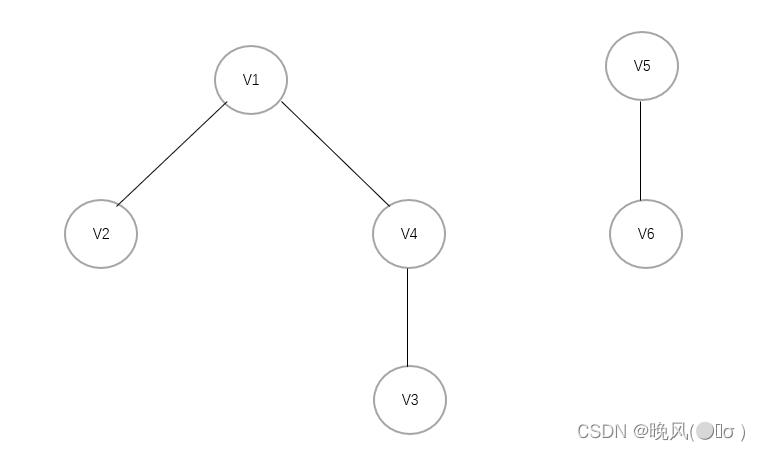
例如写出下面这个图的广度优先遍历序列：

其广度优先遍历序列为：0，4，3，2，1，6，5，9，8，7。

（三）BFS的空间复杂度和时间复杂度

对于一个图G=（V，E），由顶点集V和边集E组成。
1、BFS算法的空间复杂度

• ✨通过BFS遍历的空间复杂度为O(|V|)。

2、BFS算法的时间复杂度

• ✨时间复杂度取决于图的存储结构，若通过邻接矩阵表示图，则查找顶点的邻接顶点所需时间为O(|V|)，总时间复杂度为O(|V²|)（邻接矩阵为方阵n×n），这和DFS算法的时间复杂度是一样的；若通过邻接表表示图，则每个顶点都入队一次，即所需时间为O(|V|)，搜索顶点的邻接顶点所需时间为O(|E|)，其时间复杂度为O(|V|+|E|)。

四、DFS和BFS的应用

以上两种遍历算法都可以用于判断图的连通性，可计算图中的连通分量数目，当一个图为连通图时，经过遍历后会访问到所有的顶点，其中访问过的顶点不会再次访问，从而可以得到图中的连通分量数目。