数据与模型并行

Posted 2023-05-12

参考技术A

利用计算机集群，使机器学习算法更好地从大数据中训练出性能优良的大模型是分布式机器学习的目标。为了实现这个目标，一般需要根据硬件资源与数据/模型规模的匹配情况，考虑到计算任务、训练数据和模型进行划分，分布式存储、分布式训练。
分布式机器学习可以分为计算并行模式、数据并行模式和模型并行模式。

假设系统中的工作节点拥有共享内存（比如单机多线程环境），可以存储下数据和模型，并且每个工作节点对数据有完全地访问权限，对数据有读写权限。那么，在此类系统中实现分布式机器学习算法，对数据和模型不需要特殊处理，只需要把注意力集中在如何并行的执行相应的优化算法上。我们称这种并行模式为计算并行模式。
公式详见书中P119

数据样本划分和数据维度划分是两种常见的数据划分方法。其中，对于样本划分方法，又有随机采样和（全局/局部）置乱切分等方法。总体来说，进行数据划分时要考虑以下两个因素。
一是数据量和数据维度与本地内存的相对大小，以此判断数据按照样本划分和维度划分后能否合适地存储到本地内存
二是优化方法的特点。通常，样本划分更适合于随机抽取样本的优化方法（比如随机梯度下降法），维度划分更适用于随机抽取维度的优化方法（比如随机坐标下降法）。

那么为什么数据划分是合理的？因为在于机器学习中的目标函数，也就是训练数据集的经验风险函数，关于样本是可分的。因为经验风险函数是所有训练样本对应的损失函数取值的总和，所以如果将训练样本划分成多个数据子集，计算各个子集上的局部梯度值，再将局部梯度函数，任然可以得到整个经验风险函数的梯度值。
置乱切分相比于随机采样有以下好处：

当划分到本地的训练数据被优化算法依照顺序使用完一遍之后，有两种对数据进行再处理的方法：再次进行全局置乱切分和仅对本地数据进行局部置乱。为引用方便，我们分别称其为：“全局置乱切分”和“局部置乱切分”。
· 带有置乱切分的随机梯度下降法相比带有随机采样的随机梯度下降法，收敛速率要慢一些，这是因为置乱切分后样本不在是独立的，影响了收敛速率。
· 带有局部置乱切分的随机梯度下降法的收敛速率比带有全局置乱切分的随机梯度下降法的收敛速率慢。原因在于，局部置乱切分中，数据第一次切分之后，将不再进行全局置乱，局部数据的差异性始终保持，相比全局置乱的情形对于数据独立同分布假设的违背更加严重。

如果机器学习任务中所涉及的模型规模很大，不能存储到工作节点的本地内存，就需要对模型进行划分，然后各个工作节点负责本地局部模型的参数更新。对具有变量可分性的线性模型和变量相关性很强的非线性模型（比如神经网络），模型并行的方式有所不同。

把模型和数据按维度均等均分，分配到不同的工作节点，在每个工作节点使用坐标下降法进行优化。
对于线性模型而言，目标函数针对各个变量是可分的，也就是说某个维度的参数更新/梯度只依赖一些与目标函数值有关的全局变量，而不依赖与其他维度的参数取值。于是，为了实现本地参数的更新，我们只需要对这些全局变量进行通信，不需要对其他节点的模型参数进行通信。这是可分性模型进行模型并行的基本原理

神经网络由于具有很强的非线性，参数之间的依赖关系比线性模型严重的很多，不能进行简单的划分，也无法使用类似线性模型那样的技巧通过一个全局中间变量实现高效的模型并行，但是事务总是有两面性，神经网络的层次化借故偶也为模型并行带来了一定的便利性，比如我们可以横向按层划分、纵向跨层划分和利用神经网络参数的冗余性进行随机划分。不同划分模式对应的通信内容和通信量是不相同的。
1.横向按层划分
如果神经网络很深，一个自然并且易于实现的模型并行方法就是整个神经网络横向划分为K个部分，每个工作节点承担一层或者几层的计算任务。如果计算所需要的信息本工作节点没有，则向相应的其他工作节点请求相关的信息。模型横向划分的时候，通常我们会结合各层的节点数目，尽可能使得各个工作节点的计算量平衡。

2.纵向跨层划分
神经网络除了深度还有宽度（而且通常情况下宽度会大于深度），因此除了上一小节介绍的横向按层划分外，自然地可以纵向跨层划分网络，也就是将每一层的隐含节点分配给不同的工作节点。工作节点存储并更新这些纵向子网络。在前向和后传过程中，如果需要子模型以外的激活函数和误差传播值，向对应的工作节点请求相关信息进行通信。

实验表明：1，模型随机并行的速度比纵向按层划分快，尤其对于复杂任务下的大模型更是如此；2.选取适当的骨架比列会使并行速度进一步提高。

『AI原理解读』MindSpore1.2强大并行能力介绍与解读

---

融合 5 大维度，强大的自动并行

 

MindSpore 自动并行提供了 5 维的并行方式：数据并行、算子级模型并行、Pipeline 模型并行、优化器模型并行和重计算，并且在图编译阶段，有机融合了 5 个维度的并行。这 5 维并行方式组合起来构成了盘古的并行策略。

 

a. 数据并行

 

数据并行是最基本，应用最广的并行方式，其将训练数据（mini-batch）切分，每台设备取得其中一份；每台设备拥有完整的模型。在训练时，每台设备经过梯度计算后，需要经过设备间的梯度同步，然后才能进行模型参数的更新。

b. 算子级模型并行

 

算子级模型并行是对模型网络中的每个算子涉及到的张量进行切分。MindSpore 对每个算子都独立建模，每个算子可以拥有不同的切分策略。

以矩阵乘算子 MatMul(x, w)为例，x 是训练数据，w 是模型参数，两者都是二维矩阵。并行策略 ((4, 1), (1, 1)) 表示将 x 按行切 4 份，保持 w 不切，如果一共有 4 台设备，那么每台设备拥有一份 x 的切片，和完整的 w。

c.Pipeline 模型并行

 

Pipeline 模型并行将模型的按层分成多个 stage，再把各个 sage 映射到多台设备上。为了提高设备资源的利用率，又将 mini-batch 划分成多个 micro-batch, 这样就能够使得不同设备在同一时刻处理不同 micro-batch 的数据。

一种 Pipeline 并行方式(Gpipe) 要求反向计算要等所有设备的正向计算完成后才开始，而反向计算可能依赖于正向的输出，导致每个卡正向计算过程中累积的 activation 内存与 micro-batch 数量成正比，从而限制了 micro-batch 的数量。MindSpore 的 Pipeline 并行中，将反向提前，每个 micro-batch 计算完成后，就开始计算反向，有效降低 activation 存储时间，从而提升整体并行效率。

d. 优化器模型并行

 

优化器模型并行将优化器涉及到的参数和梯度切分到多台设备上。以 Adam 优化器为例，其内部可能有多份与权重同等大小的「动量」需要参与计算。在数据并行的情况下，每个卡都拥有完整的「动量」，它们在每个卡上都重复计算，造成了内存及计算的浪费。通过引入优化器并行，每个卡只保存权重及「动量」的切片，能降低每个卡的静态内存及提升计算效率。

e. 重计算

 

重计算 (Rematerialization) 针对正向算子的输出累计保存在内存中，导致内存峰值过大的问题，舍弃了部分正向算子的输出，而是在反向阶段用到时再重新计算一遍。这样做有效地降低了训练过程中的内存使用峰值。如下图所示，第一个内存峰值通过重计算消除，第二个内存峰值可以通过前面讲到的优化器并行消除。

有了这 5 维的并行维度后，如何将其组合起来作用于盘古，并且如何将切分后的模型分片分配到每台设备上仍然是难题。MindSpore 自动并行，把这 5 个维度并行有机组合起来，可以实现非常高效的大模型分布式训练能力

下图 (b) 是一典型的树形的硬件拓扑结构，其带宽随着树深度的增加而降低，并且会产生一些流量冲突。为了利用此特征，MindSpore 的目标是最大化计算通信比，将通信量大的并行方式（算子级并行）放置在服务器内部的多卡之间；将通信量较小（Pipeline 并行）的放置在同一机架内的服务器间；将数据并行（优化器并行）的部分放置在不同机架间，因为该通信可以和计算同时执行(overlap)，对带宽要求较低。

在盘古 2000 亿模型中，MindSpore 将 64 层（layer）划分为 16 个 stage，每个 stage 包含 4 层。在每层中，利用算子级并行的方式对张量进行切分。

如下图中的 Q,K,V 的参数在实际中（按列）被切了 8 份，输入张量（按行）被切了 16 份，输出张量因此被切了 128 份（8*16）。重计算配置是配置在每层内的，也就是重计算引入的多余的计算量不会超过一层的计算量。总计，MindSpore 使用了 2048 块昇腾处理器来训练盘古。

MindSpore 对外屏蔽了复杂并行实现的细节，使得用户像编写单机模型脚本那样简单。用户在单机脚本的基础上，仅通过少了配置就能实现多维度的混合并行。下图是简化版的盘古脚本，其中红色加粗字体表示的在 MindSpore 中的并行策略。将红色加粗字体去掉，则是单机脚本。

 

图算跨层联合优化，发挥硬件极致性能

 

除了跨节点间的大规模自动外，在单卡节点内，MindSpore 通过图层和算子层的跨层协同优化，来进一步发挥昇腾算力。

在传统的 NN 网络中，不同算子承载的计算量和计算复杂度也各不相同。如 LayerNorm 由 11 个基本算子组成，而 Add 则只有 1 个基本算子。这种基于用户角度的算子定义，通常是无法充分发挥硬件资源计算能力的。因为计算量过大、过复杂的算子，通常很难生成切分较好的高性能算子。从而降低设备利用率；而计算量过小的算子，由于计算无法有效隐藏数据搬移开销，也可能会造成计算的空等时延，从而降低设备利用率。

为了提升硬件利用率，MindSpore 使用了图算融合优化技术，通过图层和算子层联合优化，并将「用户使用角度的易用性算子」进行重组融合，然后转换为「硬件执行角度的高性能算子」，从而充分提升硬件资源利用率，进而提升整网执行性能。具体优化流程如下图所示：

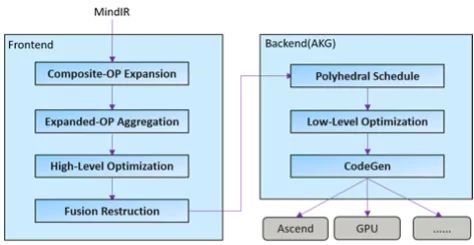
以 LayerNorm 算子为例，通过算子拆分和重组，11 个小算子，组成了 1 个单算子和 2 个融合算子。这些重组后的算子可以生成更加高性能的算子，从而大大降低了整体网络运行时间。

在盘古模型中，图算融合帮助整体训练时间减少了 20% 以上。除此之外，对于其它 NLP、CV 等任务，图算融合在优化性能方面都有不错的表现。