运用Householder矩阵证明

Posted 2023-05-12

其中x，y是n维向量。急呀，论文要用，请高手帮忙，给分多多。

这个问题一般来讲是用特征值或者Sherman-Morrison公式来做的，如果你一定需要Householder矩阵，那么这样做：
取Householder阵H使得Hx//e1，即Hx=ke1，其中e1是单位阵的第一列。那么
det(I+xy')=det(H(I+xy')H)=det(I+ke1*y'H)，
如果记z=Hy，注意到ke1*z'是非零元只在第一行出现的矩阵，所以I+ke1*z'是上三角阵，det(I+ke1*y'H)=1+k*z(1)，其中z(1)是z的第1个分量，利用z(1)=e1'z即得结论。 参考技术A 首先考察矩阵A=x*y^T
r(A)<=r(x)=1
这个矩阵的n个特征值中，必定是n-1个0，和一个<x,y>。

如果x,y的内积为0，即<x,y>=0，则A的特征值为全0，
如果x,y的内积不为0，即<x,y>不等于0，则A的特征值为（n-1）个0和一个非零数<x,y>

不管是哪种情况，A的特征值都能记为：0,0,...,0,<x,y>

所以I+A的特征值是：1,1,...,1,1+<x,y>

det(I+A)就是特征值的乘积=1*1*...*1*(1+<x,y>)
=1+<x,y>
=1+(x^T*y)

机器学习中的矩阵方法03：QR 分解

1. QR 分解的形式

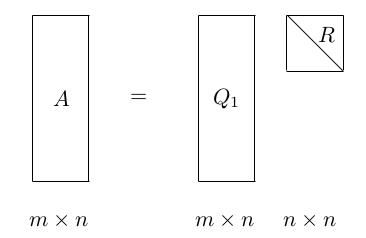
QR 分解是把矩阵分解成一个正交矩阵与一个上三角矩阵的积。QR 分解经常用来解线性最小二乘法问题。QR 分解也是特定特征值算法即QR算法的基础。用图可以将分解形象地表示成：

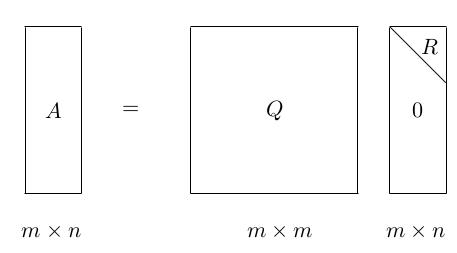
其中， Q 是一个标准正交方阵， R 是上三角矩阵。

 

2. QR 分解的求解

QR 分解的实际计算有很多方法，例如 Givens 旋转、Householder 变换，以及 Gram-Schmidt 正交化等等。每一种方法都有其优点和不足。上一篇博客介绍了 Givens 旋转和 Householder 变换， 第三种方法线性代数课程里面已经非常常见。下面用 Householder 变换的方法推导中间的过程。

假设 A 是一个 5×4 的矩阵，用 × 号表示本次变换未变化的元素，用 + 号表示本次发生变换的元素， H 矩阵等效于对右侧的 A 矩阵进行行操作：

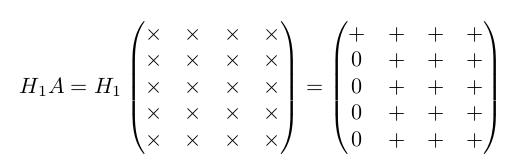
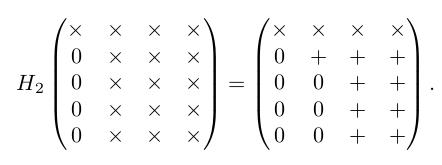
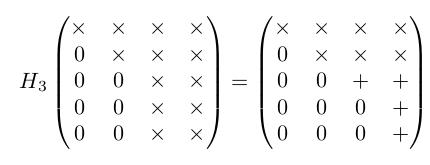
四次变换之后, A 就转化成一个上三角矩阵。并且如果 A 是列向量不相关，则 R 矩阵是非奇异矩阵。

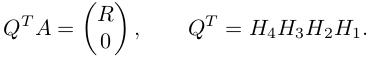
由于 H1, H2, H3, H4 都是标准化正交矩阵，那么 QT 也是标准正交矩阵。

根据矩阵相乘的性质，由于 R 下面都是 0 元素，因此，可以将 Q 矩阵对应分解成 Q1 和 Q2 两个部分，后面乘以 0 向量的部分可以省略，这就是 thin QR 分解：

上式中 R 的列向量可以看做是以 Q1 列向量为基的子空间的坐标。

 

3. 用 QR 解决最小二乘法

这个系列的第一篇博客就用 Normal equations 的方法解决了最小二乘的问题，具体来说使用了“伪逆”，但是这种做法存在缺陷，比如计算量大和浮点数运算中 roundoff 的问题。现在我们尝试用 QR 的方法来试一试。对于一个 OverDeterminded 的矩阵 A， 最小二乘的问题可以归结为：

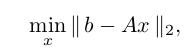
将 A 进行 QR 分解，很容易可以推导出目标函数（残差的平方）：

 

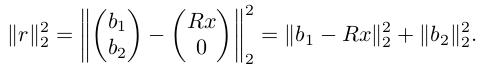
其中，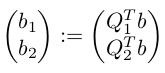 

后面一项是硬伤，没有办法优化，令前面一项等于 0, 可以得到最小二乘法的 solution:

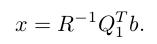
而且有一个好处是，用 Householder 变换得到的 P1, P2, P3...等，我们完全没有必要把用 Q = P1P2P3 显性地求出来，而是将 b 向量添加到 A 矩阵右侧, 与 A 一起做 Householder 变换即可：

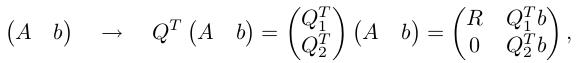
另外一个福利是：由于 Householder 变换和平面旋转变换对于浮点运算的 rounding error 问题有优良的性质，QR 分解方法比 Normal equations 的条件数更小, 某些问题的 solution 也更加精确。

 

4. 更新最小二乘的解集

在一些应用里面，系统要求我们实时更新解集，但是样本数据是逐渐产生的，也就是说矩阵 A 和向量 b 是逐渐变长的，如何在已有的解集上进行更新？

问题可以描述如下：假设现在已经将产生的数据进行了 QR 分解，新产生的数据是 a 和 beta，

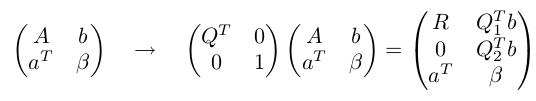
由于中间的 Q_2^T b 对于运算没有作用，我们暂且将它扔掉，用 × 表示不变的元素，用 + 表示变化的元素，我们的主要思路是用 Givens 旋转操作（上一篇博客有介绍，实际上 Householder 变换和 Givens 旋转都是左乘一个标准化的正交矩阵，在这里是等效的），先对第 1 行和第 n+1 行进行旋转，然后对第 2 行和地 n+1 行进行旋转... 一步一步求出更新后的 R 和 Q1b：

第一行和第 n+1 行进行旋转：

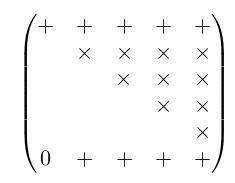
第二行和第 n+1 行进行旋转：

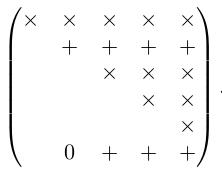
依次进行，直到：

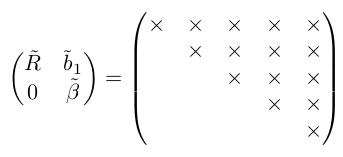
最终得到解集。

 

 

 

作者：daniel-D 出处：http://www.cnblogs.com/daniel-D/ 欢迎转载或分享，但请务必声明文章出处。