ML - 决策树(decision tree)

Posted 2023-05-10

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了ML - 决策树(decision tree)相关的知识，希望对你有一定的参考价值。

参考技术A

机器学习中分类和预测算法的评估：

判定树是一个类似于流程图的树结构：其中，每个内部结点表示在一个 属性上的测试 ，每个分支代表一个 属性输出 ，而每个树叶结点代表 类或类分布 。树的最顶层是根结点。
机器学习中分类方法中的一个重要算法

信息和抽象，如何度量？

1948年，香农提出了 ”信息熵(entropy)“的概念

一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者

是我们一无所知的事情，需要了解大量信息==> 信息量的度量就等于不确定性的多少

例子：猜世界杯冠军，假如一无所知，猜多少次？

每个队夺冠的几率不是相等的

比特(bit)来衡量信息的多少

变量的不确定性越大，熵也就越大

3.1 决策树归纳算法（ ID3 ）

1970-1980， J.Ross. Quinlan, ID3算法

选择属性（A为age时）判断结点

信息获取量(Information Gain) ：
Gain(A) = Info(D) - Infor_A(D)
Gain(A) =按yes/no分的熵 - 按A属性分类的熵

通过A来作为节点分类获取了多少信息

类似
Gain(income) = 0.029
Gain(student) = 0.151
Gain(credit_rating)=0.048
所以，选择age作为第一个根节点

重复。。。

算法：

*其他算法：

C4.5 : Quinlan

Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)

共同点：都是贪心算法，自上而下(Top-down approach)

区别：属性选择度量方法不同： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

先剪枝

后剪枝

直观，便于理解，小规模数据集有效

处理连续变量不好（离散化，阈值选择对结果影响大）

类别较多时，错误增加的比较快

可规模性一般

1. Python

2. Python机器学习的库： scikit-learn

2.1：特性：

简单高效的数据挖掘和机器学习分析

对所有用户开放，根据不同需求高度可重用性

基于Numpy, SciPy和matplotlib

开源，商用级别：获得 BSD许可

2.2 覆盖问题领域：

分类（classification), 回归（regression), 聚类（clustering), 降维(dimensionality reduction)

模型选择(model selection), 预处理(preprocessing)

3. 使用用scikit-learn

安装scikit-learn: pip, easy_install, windows installer

安装必要package：numpy， SciPy和matplotlib，可使用 Anaconda (包含numpy, scipy等科学计算常用package）

4. 例子：

文档： http://scikit-learn.org/stable/modules/tree.html

安装 Graphviz： http://www.graphviz.org/
配置环境变量
转化dot文件至pdf可视化决策树：dot -Tpdf iris.dot -o outpu.pdf

以决策树(Decision Tree)作为入门

定义 Machine Learning

"Machine Learning is the field of study that gives the computer the
ability to learn without being explicitly programmed.” – Arthur
Samuel (1959)
“A computer is said to learn from experience E with respect to some
class of task T and performance measure P, if its performance at
tasks in T , as measured by P, improved with experience E ” – Tom
Mitchel

就，没啥可多说的。第一个定义可读性更强，第二个定义专业性更强，根据个人喜好喜欢哪个就去理解哪个吧。我个人是更喜欢第二个，因为在看身为百度AI首席工程师（不知道现在还是不是）的吴恩达Deep Learning 课程的时候，他就是使用这个定义入门的，虽然比较绕口，但是确确实实是ML这个东西做事的本质。

这篇文章以及这个系列会包含很多UoA上课讲的一些内容，完全是个人学习的理解以及笔记记录，没有任何商业用途，侵必删。

Decision Tree

Make sense （建立概念）

决策树是一类常见的机器学习算法，以二分类任务为例，我们希望从给定的训练数据集学得一个模型用以新的示例进行分类，这个把样本分类的任务，可以看作“当前样本属于正类吗？”这个问题的决策或判定过程，顾名思义，决策树是基于树形结构来进行决策的，这恰是人类在面对决策问题时的一种很自然的处理机制。所以入门机器学习算法以决策树为引，的确有其优势所在。

对于一组数据（以UoA课件给出的Allergy数据为例）

决策树是一个简单的模型，由以下两部分组成：

基于特征的嵌套“if-else”序列（分裂）
在每个序列的末尾类标签会作为返回值

一个比较简单的，基于上面给定数据的决策树算法例子

以树的结构来展示会非常好理解：

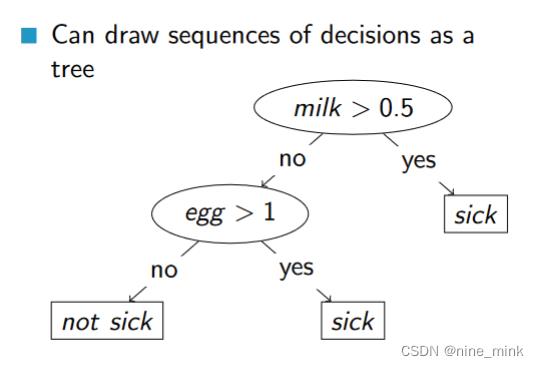
A simple decision tree creation algorithm （一个简单的决策树算法）

Greedy Recursive Splitting (贪心递归分裂)

在实践中，依据UoA的课件，最常用的算法是用分治的思想，基于贪心策略的递归生成决策树。其主要过程很简单，现在通过上面给出的Allergy数据进行模拟：

从这里似乎可以看出一点点贪心的影子，这里进行划分的贪心策略是：选取划分最终结果Sick精准度最高的一个属性（这里选的是Milk是否大于0.5）来对所有数据进行第一次划分，将所有数据划分为两个部分。

如图，这样就完成了决策树树根的创建。

接下来分别处理目前决策树仅有的两个叶子节点。

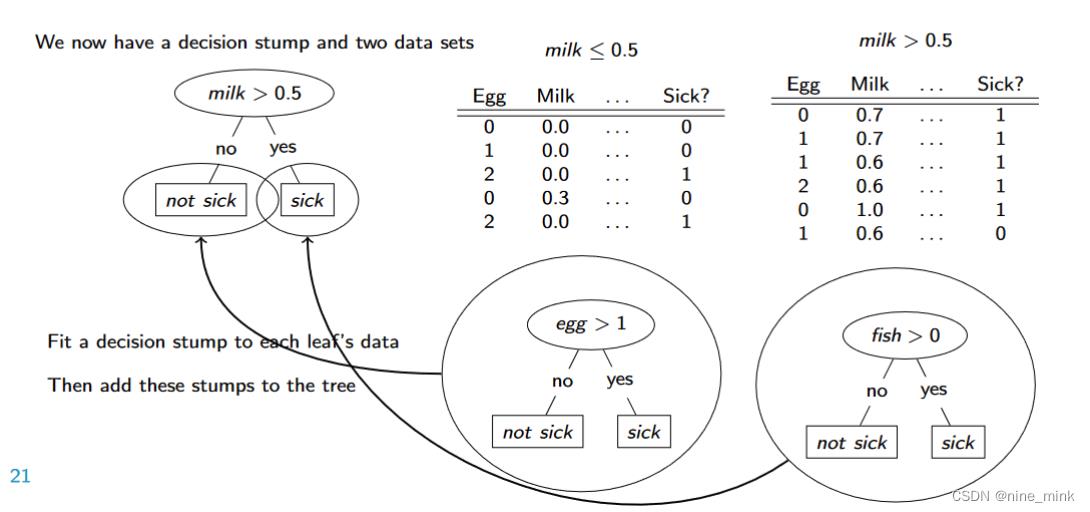
对每个叶子节点的数据，都实施以根节点相同的贪心策略，逐步划分。

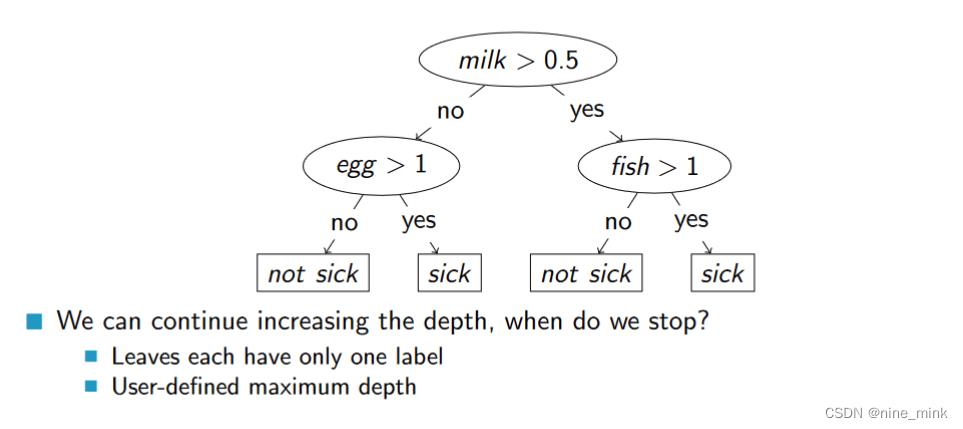
那么到了这一步，就会划分出如图所示的一颗尚未完成的决策树。每个决策树的叶子节点都只有一个标志。

在划分决策树时，可以人为地定义“超参数”——决策树的最大深度，来作为边界。

如此划分下去，不考虑过拟合以及预测准确率的一颗决策树就会被生成出来。

Fundamental algorithm of decision tree learning （决策树学习的基本算法）

一般地，一颗决策树包含一个根节点、若干个内部节点和若干个叶节点。叶子节点对应于决策结果，其他的每个节点则对应一个属性测试；每个节点包含的样本集合根据属性测试的结果被划分到叶子节点中；根节点包含样本全集，从根节点到每个叶节点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一颗泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单直观的“分而治之”的策略。

下图所示为算法伪代码

显然，决策树的生成是一个递归过程，在决策树基本算法中，有三种情形会导致递归返回：(1) 当前节点包含的样本全部属于同一类别，无需划分; (2) 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分; (3) 当前节点包含的样本集合为空，不能划分。

在第（2）中情形下，我们把当前节点标记为叶子节点，并将其类别设定为该结点所含样本最多的类别；在第（3）种情形下，同样把当前结点标记为叶子节点，但将其类别设定为其父节点所含样本最多的类别。注意这两种情形的处理实质不同：情形（2）是利用当前节点的后验分布，而情形（3）是把父亲节点的样本分布作为当前节点的先验分布。

补充：先验分布，后验分布，似然估计值的通俗解释

https://blog.csdn.net/qq_23947237/article/details/78265026

Which score function should a decision tree use?（DT算法中的划分选择）

决策树学习的最关键是如何选取最优化分属性，一般而言，随着划分的不断进行，我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度(purity)”越来越高。

信息增益

下图是西瓜书对于信息熵的定义，由于这里我的的确确是通过看西瓜书看懂的，所以UoA的课件就不放出来了

信息增益率

拿一个极端的例子来说，当数据的编号也被算作有效特征计算时，其信息增益值可能会非常大，因为每一个编号都会单独产出一个分支，这些分支结点的纯度以达到最大，然而显然这样的决策树不具备任何泛化的能力，无法对新样本进行有效的预测。

需要注意的是，增益率准则对可取值数目较少的属性有所偏好，因此C4.5 决策树算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

基尼指数

决策树经典算法

ID3算法
　　在决策树生成过程中，以信息增益为特征选择的准则。

C4.5算法
　　在决策树生成过程中，以信息增益比为特征选择的准则。

CART算法（scikit-learn中有两类决策树，它们均采用优化的CART决策树算法）
　　在决策树生成过程中，以基尼指数为特征选择的准则。

Python实现以及UoA决策树一节课后习题

Python scikit-learn 中决策树方法

'''
scikit-learn中有两类决策树，它们均采用优化的CART决策树算法。
'''
from sklearn.tree import DecisionTreeRegressor
'''
回归决策树
'''
DecisionTreeRegressor(criterion="mse",
                         splitter="best",
                         max_depth=None,
                         min_samples_split=2,
                         min_samples_leaf=1,
                         min_weight_fraction_leaf=0.,
                         max_features=None,
                         random_state=None,
                         max_leaf_nodes=None,
                         min_impurity_decrease=0.,
                         min_impurity_split=None,
                         presort=False)
'''
参数含义：
1.criterion:string, optional (default="mse")
            它指定了切分质量的评价准则。默认为'mse'(mean squared error)。
2.splitter:string, optional (default="best")
            它指定了在每个节点切分的策略。有两种切分策咯：
            (1).splitter='best':表示选择最优的切分特征和切分点。
            (2).splitter='random':表示随机切分。
3.max_depth:int or None, optional (default=None)
             指定树的最大深度。如果为None，则表示树的深度不限，直到
             每个叶子都是纯净的，即叶节点中所有样本都属于同一个类别，
             或者叶子节点中包含小于min_samples_split个样本。
4.min_samples_split:int, float, optional (default=2)
             整数或者浮点数，默认为2。它指定了分裂一个内部节点(非叶子节点)
             需要的最小样本数。如果为浮点数(0到1之间)，最少样本分割数为ceil(min_samples_split * n_samples)
5.min_samples_leaf:int, float, optional (default=1)
             整数或者浮点数，默认为1。它指定了每个叶子节点包含的最少样本数。
             如果为浮点数(0到1之间)，每个叶子节点包含的最少样本数为ceil(min_samples_leaf * n_samples)
6.min_weight_fraction_leaf:float, optional (default=0.)
             它指定了叶子节点中样本的最小权重系数。默认情况下样本有相同的权重。
7.max_feature:int, float, string or None, optional (default=None)
             可以是整数，浮点数，字符串或者None。默认为None。
             (1).如果是整数，则每次节点分裂只考虑max_feature个特征。
             (2).如果是浮点数(0到1之间)，则每次分裂节点的时候只考虑int(max_features * n_features)个特征。
             (3).如果是字符串'auto',max_features=n_features。
             (4).如果是字符串'sqrt',max_features=sqrt(n_features)。
             (5).如果是字符串'log2',max_features=log2(n_features)。
             (6).如果是None，max_feature=n_feature。
8.random_state:int, RandomState instance or None, optional (default=None)
             (1).如果为整数，则它指定了随机数生成器的种子。
             (2).如果为RandomState实例，则指定了随机数生成器。
             (3).如果为None，则使用默认的随机数生成器。
9.max_leaf_nodes:int or None, optional (default=None)
             (1).如果为None，则叶子节点数量不限。
             (2).如果不为None，则max_depth被忽略。
10.min_impurity_decrease:float, optional (default=0.)
             如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease，则分裂该节点。
             个人理解这个参数应该是针对分类问题时才有意义。这里的不纯度应该是指基尼指数。
             回归生成树采用的是平方误差最小化策略。分类生成树采用的是基尼指数最小化策略。
             加权不纯度的减少量计算公式为：
             min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity
                                - N_t_L / N_t * left_impurity)
             其中N是样本的总数，N_t是当前节点的样本数，N_t_L是分裂后左子节点的样本数，
             N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数，right_impurity指
             分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。
11.min_impurity_split:float
             树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值，节点将分裂，否则它是叶子节点。
             这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。
12.presort： bool, optional (default=False)
             指定是否需要提前排序数据从而加速寻找最优切分的过程。设置为True时，对于大数据集
             会减慢总体的训练过程；但是对于一个小数据集或者设定了最大深度的情况下，会加速训练过程。
属性：
1.feature_importances_ : array of shape = [n_features]
             特征重要性。该值越高，该特征越重要。
             特征的重要性为该特征导致的评价准则的（标准化的）总减少量。它也被称为基尼的重要性
2.max_feature_:int
             max_features推断值。
3.n_features_：int
             执行fit的时候，特征的数量。
4.n_outputs_ : int
             执行fit的时候，输出的数量。
5.tree_ : 底层的Tree对象。
Notes：
控制树大小的参数的默认值（例如``max_depth``，``min_samples_leaf``等）导致完全成长和未剪枝的树，
这些树在某些数据集上可能表现很好。为减少内存消耗，应通过设置这些参数值来控制树的复杂度和大小。
方法：
1.fit(X,y):训练模型。
2.predict(X):预测。
'''
 
from sklearn.tree import DecisionTreeClassifier
'''
分类决策树
'''
DecisionTreeClassifier(criterion="gini",
                 splitter="best",
                 max_depth=None,
                 min_samples_split=2,
                 min_samples_leaf=1,
                 min_weight_fraction_leaf=0.,
                 max_features=None,
                 random_state=None,
                 max_leaf_nodes=None,
                 min_impurity_decrease=0.,
                 min_impurity_split=None,
                 class_weight=None,
                 presort=False)
'''
参数含义：
1.criterion:string, optional (default="gini")
            (1).criterion='gini',分裂节点时评价准则是Gini指数。
            (2).criterion='entropy',分裂节点时的评价指标是信息增益。
2.max_depth:int or None, optional (default=None)。指定树的最大深度。
            如果为None，表示树的深度不限。直到所有的叶子节点都是纯净的，即叶子节点
            中所有的样本点都属于同一个类别。或者每个叶子节点包含的样本数小于min_samples_split。
3.splitter:string, optional (default="best")。指定分裂节点时的策略。
           (1).splitter='best',表示选择最优的分裂策略。
           (2).splitter='random',表示选择最好的随机切分策略。
4.min_samples_split:int, float, optional (default=2)。表示分裂一个内部节点需要的做少样本数。
           (1).如果为整数，则min_samples_split就是最少样本数。
           (2).如果为浮点数(0到1之间)，则每次分裂最少样本数为ceil(min_samples_split * n_samples)
5.min_samples_leaf: int, float, optional (default=1)。指定每个叶子节点需要的最少样本数。
           (1).如果为整数，则min_samples_split就是最少样本数。
           (2).如果为浮点数(0到1之间)，则每个叶子节点最少样本数为ceil(min_samples_leaf * n_samples)
6.min_weight_fraction_leaf:float, optional (default=0.)
           指定叶子节点中样本的最小权重。
7.max_features:int, float, string or None, optional (default=None).
           搜寻最佳划分的时候考虑的特征数量。
           (1).如果为整数，每次分裂只考虑max_features个特征。
           (2).如果为浮点数(0到1之间)，每次切分只考虑int(max_features * n_features)个特征。
           (3).如果为'auto'或者'sqrt',则每次切分只考虑sqrt(n_features)个特征
           (4).如果为'log2',则每次切分只考虑log2(n_features)个特征。
           (5).如果为None,则每次切分考虑n_features个特征。
           (6).如果已经考虑了max_features个特征，但还是没有找到一个有效的切分，那么还会继续寻找
           下一个特征，直到找到一个有效的切分为止。
8.random_state:int, RandomState instance or None, optional (default=None)
           (1).如果为整数，则它指定了随机数生成器的种子。
           (2).如果为RandomState实例，则指定了随机数生成器。
           (3).如果为None，则使用默认的随机数生成器。
9.max_leaf_nodes: int or None, optional (default=None)。指定了叶子节点的最大数量。
           (1).如果为None,叶子节点数量不限。
           (2).如果为整数，则max_depth被忽略。
10.min_impurity_decrease:float, optional (default=0.)
         如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease，则分裂该节点。
         加权不纯度的减少量计算公式为：
         min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity
                            - N_t_L / N_t * left_impurity)
         其中N是样本的总数，N_t是当前节点的样本数，N_t_L是分裂后左子节点的样本数，
         N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数，right_impurity指
         分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。
11.min_impurity_split:float
         树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值，节点将分裂，否则它是叶子节点。
         这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。
12.class_weight:dict, list of dicts, "balanced" or None, default=None
         类别权重的形式为class_label: weight
         (1).如果没有给出每个类别的权重，则每个类别的权重都为1。
         (2).如果class_weight='balanced'，则分类的权重与样本中每个类别出现的频率成反比。
         计算公式为：n_samples / (n_classes * np.bincount(y))
         (3).如果sample_weight提供了样本权重(由fit方法提供)，则这些权重都会乘以sample_weight。
13.presort:bool, optional (default=False)
        指定是否需要提前排序数据从而加速训练中寻找最优切分的过程。设置为True时，对于大数据集
        会减慢总体的训练过程；但是对于一个小数据集或者设定了最大深度的情况下，会加速训练过程。
属性:
1.classes_:array of shape = [n_classes] or a list of such arrays
        类别的标签值。
2.feature_importances_ : array of shape = [n_features]
        特征重要性。越高，特征越重要。
        特征的重要性为该特征导致的评价准则的（标准化的）总减少量。它也被称为基尼的重要性
3.max_features_ : int
        max_features的推断值。
4.n_classes_ : int or list
        类别的数量
5.n_features_ : int
        执行fit后，特征的数量
6.n_outputs_ : int
        执行fit后，输出的数量
7.tree_ : Tree object
        树对象，即底层的决策树。
方法:
1.fit(X,y):训练模型。
2.predict(X):预测
3.predict_log_poba(X):预测X为各个类别的概率对数值。
4.predict_proba(X):预测X为各个类别的概率值。
'''

Question 1

Explain how entropy is calculated. （解释信息熵如何计算）

It assumes that if in the current sample set the proportion of sample k is p[k] (k=1, 2, … , |Y|), the information entropy of D is the negative mathmatical expextion of log2(p[k])
假定当前样本集合D中第k类样本所占的比例为p[k] (k=1, 2, … , |Y|) 则D的信息熵为log2(p[k])的数学期望的相反数

What do Entropy = 1 and Entropy = 0 mean? （Entropy==1或0的时候意味什么）

(1) When D is equal with 1, the current sample set has no sample which are mutally identical.
当D=1的时候，当前样本集合不包含互为相同类别的样本
(2) When D is equal with 0, the current sample set has samples which are all mutally identical.
当D=0的时候，当前样本集合的样本都是同一类别

Explain what overfit and underfit are and how they relate to decision tree pruning. （解释什么是过拟合和欠拟合，以及它们与决策树修剪的关系）

(1) Underfit means both test error and train error are very high. Underfit means the decision tree module porforms badly in both train set and test set.
欠拟合是指模型在训练集和测试集上均表现不佳的情况；
(2) Overfit means train error is excellent but test error is bad. Overfit means the decision tree module porforms excellently in train set but not test set.
过拟合是指模型在训练集上表现很好，到了验证和测试阶段就很差，即模型的泛化能力很差。
(3) Pruning is one of the most important approach to deal with overfit
剪枝是应对过拟合的有效手段。

Discuss how the size of a decision tree affects its performance. If four decision trees aretrained on a dataset, including a baseline rule (R0), using only one variable (R1), a prunedtree, and an unpruned tree; （讨论决策树的大小如何影响其性能。如果在一个数据集上训练四棵决策树，包括一个基线规则(RO)，只使用一个变量(R1)、一棵修剪树和一棵未修剪树;）
(a) What differences in performance can be expected? （可以期待有什么不同的表现）
(b) Which trees are more likely to underfit or overfit the data? （哪一棵树最有可能过拟合或欠拟合）

Question 2

2.1 Create a decision tree manually （手动创建决策树）
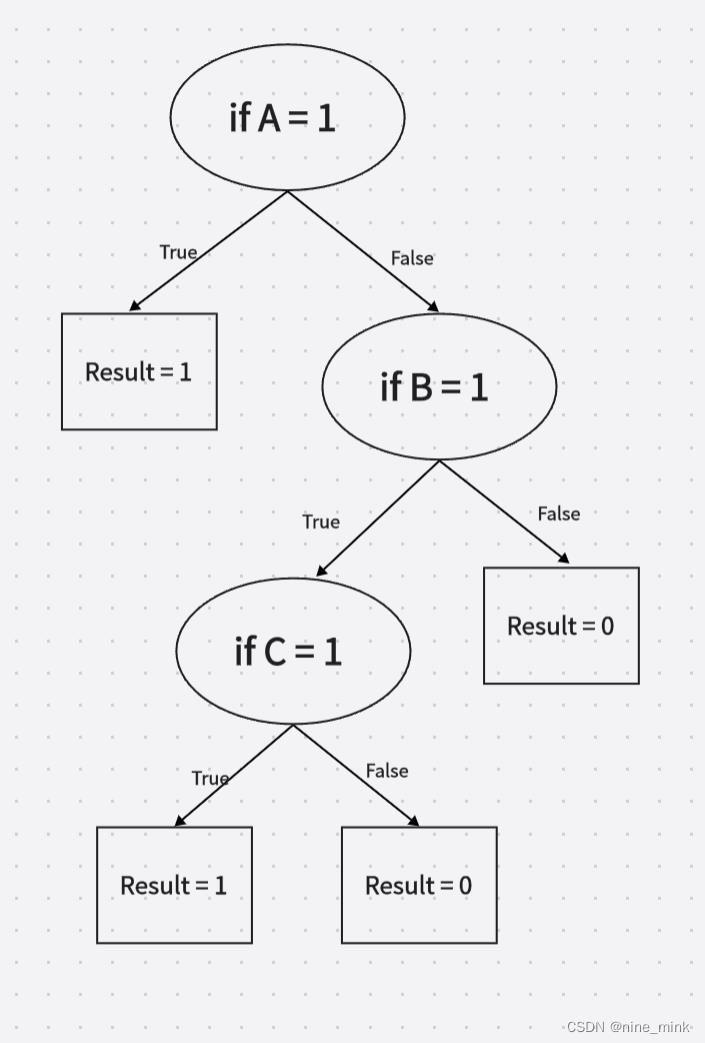
Answer the following questions and create a decision tree for the Boolean function A ∨ (B ∧ C),
using information gain and entropy:
（回答以下问题，并使用信息增益和信息熵为布尔函数A v (B ∧ C)创建决策树:）

Logical operator table：

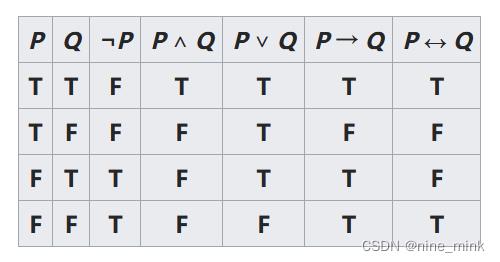
Create a table with all combinations. （创建一个包含所有组合的表）

A	B	C	A ∨ (B ∧ C)
0	0	0	0
0	0	1	0
0	1	1	1
1	1	1	1
1	0	0	1
1	1	0	1
1	0	1	1
0	1	0	0

Compute the root entropy without any prior. （计算没有任何先验的根的熵）

Setting this set as D, and then
Entropy(D) = - (3/8 * log2(3/8) + 5/8 * log2(5/8) ) = 0.954

Find the decision stump with the best score. （找到得分最高的决策树桩）

A
Ent(Da[0]) = -(1/4 * log2(1/4) + 3/4 * log2(3/4)) = 0.811
Ent(Da[1]) = 0
Gain(Da) = Ent(D) - (1/2)*0.811 = 0.5485

B
Ent(Db[0]) = -(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1
Ent(Db[1[) = -(1/4 * log2(1/4) + 3/4 * log2(3/4)) = 0.811
Gain(Db) = Ent(D) - (1/2)*1-(1/2)*0.811 = 0.0485

C
Ent(Dc[0]) = -(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1
Ent(Dc[1]) = -(1/4 * log2(1/4) + 3/4 * log2(3/4)) = 0.811
Gain(Dc) = Ent(D) - (1/2)*1-(1/2)*0.811 = 0.0485

So Gain(Da)>Gain(Db) and Gain(Da)>Gain(Dc)
So the best feature is A

Split into two subsets based on the stump. （根据树桩分成两个子集）

Set 1

B	C	A ∨ (B ∧ C)
0	0	0
0	1	0
1	1	1
1	0	0

Set 2

A	B	C	A ∨ (B ∧ C)
1	1	1	1
1	0	0	1
1	1	0	1
1	0	1	1

Keep finding the next decision stump until you obtain the complete decision tree. （继续寻找下一个决策树桩，直到获得完整的决策树）

2.2 Coding Practice
Answer the question above using the DecisionTreeClassifier method from sklearn. Plot the decision
tree and compare it with your answer from question 2.1. （使用sklearn中的DecisionTreeClassifier方法回答上面的问题。画出决策树，并将其与问题2.1的答案进行比较）

# 导入所需要的模块
from sklearn import tree #树的模块
import graphviz


X_train = [
    [0, 0, 0],
    [0, 0, 1],
    [0, 1, 1],
    [1, 1, 1],
    [1, 0, 0],
    [1, 1, 0],
    [1, 0, 1],
    [0, 1, 0]
]

Y_train = [0, 0, 1, 1, 1, 1, 1, 0]

dt = tree.ExtraTreeClassifier(criterion="entropy")

dt = dt.fit(X_train, Y_train)

feature_name = ['A', 'B', 'C']



dot_data = tree.export_graphviz(dt #训练好的模型
                                ,out_file = None
                                ,feature_names= feature_name
                                ,class_names=["琴酒","雪莉","贝尔摩德"]
                                ,filled=True #进行颜色填充
                                ,rounded=True #树节点的形状控制
)
graph = graphviz.Source(dot_data)

graph.view()

Question 3 (The same as Q2)

3.1 Create a decision tree manually （手动创建决策树）
Create a decision tree for Table 1 using information gain and entropy:
（使用表1的信息的信息熵和信息增益创建一颗决策树）

3.2 Coding Practice
Answer the question above using the DecisionTreeClassifier method from sklearn. Plot the decision
tree and compare it with your answer from question 3.1. （使用sklearn中的DecisionTreeClassifier方法回答上面的问题。画出决策树，并将其与问题3.1中的答案进行比较）

由于sklearn中的决策树算法都是进行优化过的，本身过拟合或欠拟合的情况就比较少，而且在UoA的课上剪枝并没有讲算法，所以在此并不进行实现

剪枝（Pruning）

预剪枝pre-pruning

预剪枝就是在树的构建过程（只用到训练集），设置一个阈值（样本个数小于预定阈值或GINI指数小于预定阈值），使得当在当前分裂节点中分裂前和分裂后的误差超过这个阈值则分列，否则不进行分裂操作。所有决策树的构建方法，都是在无法进一步降低熵的情况下才会停止创建分支的过程，为了避免过拟合，可以设定一个阈值，熵减小的数量小于这个阈值，即使还可以继续降低熵，也停止继续创建分支。但是这种方法实际中的效果并不好。

在划分之前，所有样本集中于根节点，若不进行划分，该节点被标记为叶节点，其类别标记为训练样例最多的类别。若进行划分在测试集上的准确率小于在根节点不进行划分的准确率，或增幅没有超过阈值，都不进行划分，作为一个叶节点返回当前数据集中最多的标签类型。

优点：快速，可以在构建决策树时进行剪枝，显著降低了过拟合风险。由于预剪枝不必生成整棵决策树，且算法相对简单，效率很高，适合解决大规模问题。但是尽管这一方法看起来很直接，但是怎样精确地估计何时停止树的增长是相当困难的。

缺点：预剪枝基于贪心思想，本质上禁止分支展开，给决策树带来了欠拟合的风险。因为视野效果问题。也就是说在相同的标准下，也许当前的扩展会造成过度拟合训练数据，但是更进一步的扩展能够满足要求，也有可能准确地拟合训练数据。这将使得算法过早地停止决策树的构造。

后剪枝post-pruning

决策树构造完成后进行剪枝。剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，熵的增加量是否小于某一阈值。如果确实小，则这一组节点可以合并一个节点，其中包含了所有可能的结果。后剪枝是目前最普遍的做法。

后剪枝的剪枝过程是删除一些子树，然后用其叶子节点代替，这个叶子节点所标识的类别通过大多数原则(majority class criterion)确定。所谓大多数原则，是指剪枝过程中, 将一些子树删除而用叶节点代替,这个叶节点所标识的类别用这棵子树中大多数训练样本所属的类别来标识。相比于前剪枝，后剪枝方法更常用，是因为在前剪枝方法中精确地估计何时停止树增长很困难。

优点：欠拟合风险小，泛化性能好。

缺点：在生成决策树之后完成，自底向上对所有非叶节点进行逐一考察，训练的时间开销较大。