如何理解矩阵相乘的几何意义或现实意义

Posted 2023-05-05

矩阵相乘，其几何意义就是两个线性变换的复合，比如A矩阵表示旋转变换，B矩阵表示伸长变换，AB就是伸长加旋转的总变换：同时伸长和旋转。

其现实意义的例子，汽车生产线上的机械手有几个关节，每个关节的转动都可看作一个空间转动矩阵，最后机械手末端的位置就是所有关节矩阵连乘（联动）的结果。

矩阵是线性变换的表示，矩阵乘以一个向量等于对这个向量施加此矩阵代表的线性变换。这种线性变换通过变换基来实现，矩阵中的各列就是变换后的新基。两个矩阵相乘，AB，就是把B中各列代表的“新基”又经过了A代表的线性变换得到了一组“新新基”。实际就是B线性变换和A线性变换的复合。

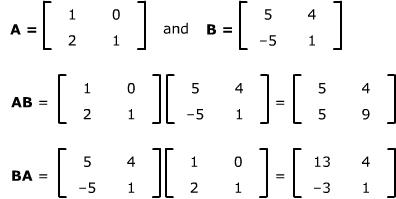
扩展资料：

矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义。一般单指矩阵乘积时，指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。

两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。更抽象的说，一个矩阵可以表示一种线性变换。很多同学在学线性代数时对矩阵相乘的方法感到奇怪，但是如果明白了矩阵相乘的物理意义，其合理性就一目了然了。

参考资料：百度百科-矩阵乘法

参考技术A 思索很久，终于明白了。 矩阵是一个线性变换 ，就是对一个向量进行拉伸和变换，是通过矩阵的变换基完成的。如果以矩阵的行向量作为变换基。例如，x轴变换基负责对向量的x维度数据(x,0)进行变换，y轴变换基负责对y维度向量（0，y）进行变换，那么假如变换基是单位向量,那么长度不变，如果不是，那肯定变了。理解难点：其实任何一个向量(x,y)都可以表示为(x,0)+(0,y)。所以所谓的线性变换，本质上就是利用矩阵的变换基对各个向量分量进行变换本回答被提问者采纳

矩阵乘法的几何意义

从投影的角度理解矩阵乘法：

向量x在以a_i作为每个坐标轴单位向量的新坐标系的坐标

通俗讲：在矩阵中，以矩阵中的行矩阵作为一个具体的点和原点的连线作为坐标轴，所有的行也是这样从而组成一个坐标系，求原来向量在新的坐标系中的坐标点。

特点：根据矩阵中的行组成的坐标系

从坐标映射角度理解矩阵乘法：变换前的区域进行旋转和沿特定方向缩放结合一起的操作，让原来区域经过形变后映射到一个新的区域中，从而求向量在新的区域中的坐标（将原来的坐标轴映射到新的坐标轴中,例如笛卡尔坐标转化成别的坐标）

特点：根据矩阵中的列组成的坐标系

新知识点：

偏置：位移向量，能将图片进行耦合的向量。作用：能够将所有的点全部耦合

仿射变换：线性变化加上一个位移向量

拟合：将所有的点以曲线的方式进行连接，从而形成图片的过程