高效空间数据索引R树及其批量加载方法STR简介
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高效空间数据索引R树及其批量加载方法STR简介相关的知识,希望对你有一定的参考价值。
参考技术A工作中经常需要跟空间数据打交道,因此频繁使用一个工具类 com.vividsolutions.jts.index.strtree.STRtree 。STRtree类似于一个集合,向其插入一些带空间信息的数据后可以很便利地按范围查询空间数据,如下图示意。
由于不清楚STRtree的查询实现逻辑,为探明原因及避免后续踩坑了解了一下,发现STRtree应用了非常精巧且应用广泛的空间索引结构R树(R-Tree)及优秀的批量加载算法STR。下文我们将从R树开始介绍,进一步了解STR算法,并说明一些STRtree相关的注意事项。
R树是一种层次数据结构,它是B树在k维空间上的自然扩展,因此和B树一样,R树是一种高度平衡树,在叶结点中包含指向实际数据对象的指针。
定义:
简单来说,R树种的每个节点都是一个矩形,而且是节点数据的最小外接矩形(MBR,Minimun Bounding Rectangle),即覆盖内部几何图形的最小矩形边界。
MBR本身通过x、y坐标容易计算,计算MBR相交也十分简单高效,适用于应用在索引结构中。
其中,叶子结点为实际结点空间数据的MBR;非叶子结点则为其所有子节点形成的MBR,即刚好包裹住所有子节点。
从定义中可以看出来,其结构与B树类似:
简单的部分到此为止,R树具体的插入删除规则涉及到复杂的规则,在节点分裂和合并之外还涉及父节点MBR的调整等,详情可参考原论文或 其他资料 。
在不使用R树时,最基础的范围搜索方法是遍历整个数据集,将所有落在范围内的数据返回,在较大数据集中这个代价显然是不可接受的。当然通过网格划分数据集的方式也可以大大缩小候选数据集,但仍需要遍历候选网格的全量数据。
而R树的搜索算法则类似B树,从根节点开始,根据搜索范围找到命中的节点,并不断向下查找到叶子结点,缩小范围,最终返回命中的数据。这非常易于理解:当我们要找到某个商场时,思考路径也是AA市->BB区->CC路->DD路口依次缩小范围。
但R树与B树最显著的区别在于R树在非一维空间使用MBR描述节点的上下界,无法像B树节点一样准确适应子节点的分布。虽然通过通过MBR提高了计算和求交的效率,不过这也势必牺牲了空间利用率(父节点包含了空白区域)及查询效率(兄弟节点MBR可能会重叠)。
在查询时,以下常见的情况会导致需要多路径搜索:
现在我们可以理解,R树中的R表示Rectangle,也表明其本质是一组有层次关系的“矩形”,在一维空间是线结构,在没有重叠的情况下结构很像B树,推广到三维则是长方体。
R树作为一个比较宽泛的结构定义,并未限定具体的构造方式,而基于R树的概念及各种组织方式衍生出了庞大的R树家族,不同组织方式的R树变体性能差距很大。其他比较有特点的一些变体索引结构:
通常从空树开始构建整个R树时,将记录逐个插入直至生成整个树的过程中会频繁触发索引结构的动态维护,这对于海量空间数据的初始化而言耗时巨大,代价过高。由此发展而来的Packing(批量加载)算法则可以在数据已知且相对静态的情况下尽可能提高R树的构建速度并优化索引结构。
其中Leutenegger等提出了一种STR(Sort-Tile-Recursive,递归网格排序) Packing算法,该算法易于实现且适用范围较广,在大多数场景下表现良好,且易于推广到高维空间。
STR算法本质上只是R树的一种构建算法,STR R-Tree本质上仍是R树。
STR可以理解为切蛋糕,首先确定一共应该切成N份,然后从左到右根据蛋糕上草莓个数竖切成sqrt(N)个中份,再从上到下把每个中份横切成sqrt(N)个小份,一趟递归就完成了。下一趟则是将小份蛋糕当作草莓,继续切直到不需要切为止,自下而上递归构成R树。
具体细节可以查看 作者原论文 ,算法介绍不到一页,概念好理解。
STR本身逻辑并不复杂,其排序和网格化的逻辑是与维度无关的,还可以拆分至按维度计算,对算法实现比较友好,构建效率也高;同时,其使用递归和网格化的思路可以较好地将兄弟MBR大致分离,尽可能减少重叠区域,大多数数据分布下查询效率较高。
R-Trees - A Dynamic Index Structure for Spatial Searching
STR: A Simple and Efficient Algorithm for R-Tree Packing
R树家族的演变和发展 - 中国科学院
空间数据索引RTree(R树)完全解析及Java实现 - 佳佳牛 - 博客园
mysql :: MySQL 5.7 Reference Manual :: 11.4.9 Creating Spatial Indexes
索引及其原理
文件系统:柱面。磁道。扇区 (确定文件地址)
索引:一种数据结构,帮助高效获取数据的数据结构
id addr
1 0x1234
2 0x3242 直接定位
如果没有索引,则从文件中一个个读取,然后比对,所以可能会发展成全盘扫描。但如果有索引的话,可以直接读取文件地址,然后找到该数据对应的磁盘地方。获得数据。
二者其实原理一样,
索引也可能是一个文件
其他类型:
hash Map
二叉平衡树
二叉树:

红黑树:
B tree
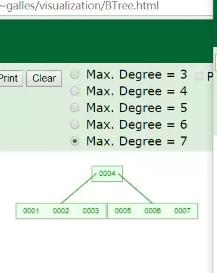
树的高度:degree
B+tree
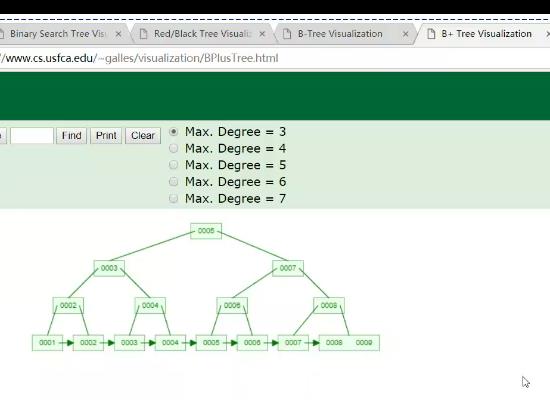
衡量索引优劣的标尺:
i/o次数(查询次数)
mysql索引:B+tree 便于查询
非聚集索引: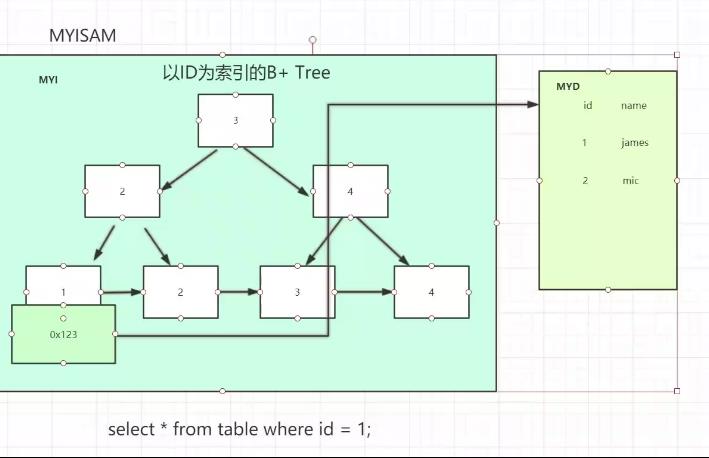
通过index查找到地址,找到value
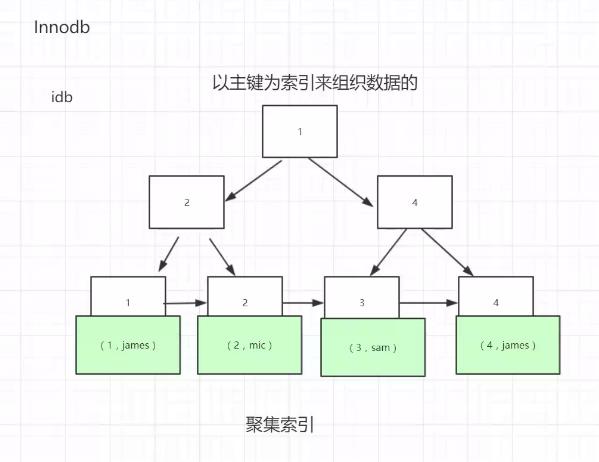
//二分法如果用于两个都是按照相同项来进行同步升序(或者降序),此时随便用哪一个作为循环外体
//如果两个判断项不同步,那么最好外体用无序,内部按照具体需要的顺序来(所要求的那个项),但其实如果反过来也可以
//optionList 为升序排列
//最重要的一点是两个循环体之间的对应关系,谁对谁是一对多还是多对一或者一对一
//如果是多对一的多的一方,那么应该循环多的一方,一的一方在循环体内,并且一的一方需要按照相等的项进行排序才可以(多应该去一的里面找,循环一)
public SurveyItemOption commonBinary(List<SurveyItemOption> optionList,SurveyItemWrapper wrapper){
Long realValue = wrapper.getItemId();
int left=0,right=optionList.size()-1;
while(left<=right){
int middle=(left+right)/2;
if(optionList.get(middle).getItemId() == wrapper.getItemId()) return optionList.get(middle);
if(realValue > optionList.get(middle).getItemId()) left=middle+1;
else right=middle-1;
}
return null;
}
//冒泡排序
public int[] bubbleSort(int[] arr){
int temp;
for ( int i =arr.length-1; i >= 0 ; i-- ) {
for ( int j = 0; j < i ; j++ ) {
if(arr[j]>arr[j+1]){
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
return arr;
}
快速排序:
//快速排序
public List<Integer> quickSort(List<Integer> list){
if(list.size()<2) return list;
final int index = list.get(0);
final ArrayList<Integer> begin = new ArrayList<Integer>();
final ArrayList<Integer> end = new ArrayList<Integer>();
int choice;
for(int i=1;i<list.size();i++){
choice = list.get(i);
if(choice<index) begin.add(choice);
else{
end.add(choice);
}
}
ArrayList resultList = (ArrayList) quickSort(begin);
resultList.add(index);
resultList.addAll(quickSort(end));
return resultList;
}
以上是关于高效空间数据索引R树及其批量加载方法STR简介的主要内容,如果未能解决你的问题,请参考以下文章