算方差的时候 为啥有的是除n 有的是除n-1 得出的数能一样吗？

Posted 2023-05-03

样本是除n-1 总体是n 怎么回事？ 不理解
最好能详细些 谢谢

当n很大时二者几乎相同。但n较小时例如5以下，就会有较大差别。
方差或标准差是反映一组数据的离散程度。运用统计原理可以导出方差（数据服从正态分布，n趋于无穷大）的计算公式（除以n）。但n有限时，分布将偏离正态分布（实际分布是t分布），偶然因素的影响会更大一些（离散程度更大），除以n-1就是考虑了n有限的情形更加合理地估计离散程度。
数学上说总体的意义是所有可能出现的值（即n趋于无穷大，例如测量一个物体长度的所有可能测量值），样本是其中某些值（n有限，例如对一个长度进行几次测定的值）。 参考技术A n个数的方差就除以n,
(n-1)个数的方差就除以(n-1)

样本方差的无偏估计与（n-1）的由来

原文出处： http://blog.sina.com.cn/s/blog_c96053d60101n24f.html

在PCA算法中用到了方差，协方差矩阵，其中方差公式为，协方差矩阵公式为，当时不明白为什么除的不是m，而是m-1，那么想要知道为何，下面就是你想要的答案。

    假设X为独立同分布的一组随机变量，总体为M，随机抽取N个随机变量构成一个样本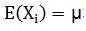，和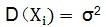是总体的均值和方差, 是常数。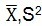是对样本的均值和方差，由于样本是随机抽取的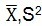，也是随机的。

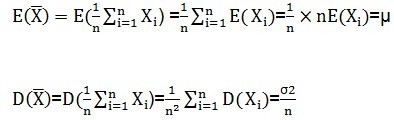
    这里需要注意的是，由于样本是随机的，所以X₁，X₂，X₃...都是随机的。上式中可以看出，样本均值这个变量的期望就是总体的均值，因此可以说均值是无偏的。

    接下来看样本方差的均值：

 

    根据方差公式，可以得到：

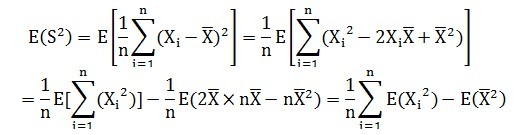
    因此：

    

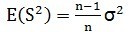
    这里可以看出样本方差的期望并不是无偏的，要无偏估计，应该再乘上一个系数：

。

    n-1既为自由度，就是说，在一个容量为n的样本里，当确定了n-1个变量以后，第n个变量就确定了，因为样本均值是无偏的。
    协方差除以m-1原理和方差一样，因为方差为协方差的特殊情况。

这个知乎上的讨论更加透彻:

http://www.zhihu.com/question/20099757