matlab抽样法恢复信号的最大恢复误差这3怎么计算

Posted 2023-05-01

matlab对信号抽样,matlab信号抽样与恢复

1、实验⼀ 信号抽样与恢复⼀、实验⽬的学会⽤MATLAB实现连续信号的采样和重建⼆、实验原理1抽样定理若是带限信号，带宽为, 经采样后的频谱就是将的频谱 在频率轴上以采样频率为间隔进⾏周期延拓。因此，当时，不会发⽣频率混叠；⽽当 < 时将发⽣频率混叠。2信号重建经采样后得到信号经理想低通则可得到重建信号，即：=*其中：=所以：=*=*=上式表明，连续信号可以展开成抽样函数的⽆穷级数。利⽤MATLAB中的来表⽰，有 ，所以可以得到在MATLAB中信号由重建的表达式如下：=我们选取信号=作为被采样信号，当采样频率=2时，称为临界采样。我们取理想低通的截⽌频率=。下⾯程序实现对信号=的采样及由该采样信号。

2、恢复重建：三、上机实验内容1验证实验原理中所述的相关程序；2设f(t)=0.5*(1+cost)*(u(t+pi)-u(t-pi) ，由于不是严格的频带有限信号，但其频谱⼤部分集中在0，2之间，带宽wm可根据⼀定的精度要求做⼀些近似。试根据以下两种情况⽤ MATLAB实现由f(t)的抽样信号fs(t)重建f(t) 并求两者误差，分析两种情况下的结果。(1) wm=2 , wc=1.2wm , Ts=1;(2) wm=2 , wc=2 , Ts=2.53对以下simulink ch6example1_He7.mdl低通采样定理以程序实现，具体参数参考框图内参数。五参考程序例1-1 Sa(t)的临。

3、界采样及信号重构；wm=1; %信号带宽wc=wm; %滤波器截⽌频率Ts=pi/wm; %采样间隔ws=2*pi/Ts; %采样⾓频率 n=-100:100; %时域采样电数nTs=n*Ts %时域采样点f=sinc(nTs/pi);Dt=0.005;t=-15:Dt:15;fa=f*Ts*wc/pi*sinc(wc/pi)*(ones(length(nTs),1)*t-nTs*ones(1,length(t); %信号重构t1=-15:0.5:15;f1=sinc(t1/pi);subplot(211);stem(t1,f1);xlabel(kTs);ylabel(f(kTs);title。

4、(sa(t)=sinc(t/pi)的临界采样信号);subplot(212);plot(t,fa)xlabel(t);ylabel(fa(t);title(由sa(t)=sinc(t/pi)的临界采样信号重构

sa(t);grid；例1-2 Sa(t)的过采样及信号重构和绝对误差分析程序和例4-1类似，将采样间隔改成Ts=0.7*pi/wm , 滤波器截⽌频率该成

wc=1.1*wm ，添加⼀个误差函数wm=1;wc=1.1*wm; Ts=0.7*pi/wm;ws=2*pi/Ts;n=-

100:100;nTs=n*Tsf=sinc(nTs/pi);Dt=0.005;t=-15:Dt:15;fa=f。

5、*Ts*wc/pi*sinc(wc/pi)*(ones(length(nTs),1)*t-nTs*ones(1,length(t);error=abs(fa-sinc(t/pi); %重构信号与原信号误差t1=-

15:0.5:15;f1=sinc(t1/pi);subplot(311);stem(t1,f1);xlabel(kTs);ylabel(f(kTs);title(sa(t)=sinc(t/pi)的采样信

号);subplot(312);plot(t,fa)xlabel(t);ylabel(fa(t);title(由sa(t)=sinc(t/pi)的过采样信号重构

sa(t);grid;subplot(313);plot(t,error);xlabel(t);ylabel(error(t);title(过采样信号与原信号的误差error(t)；例1-3 Sa(t)的⽋采样及信号重构和绝对误差分析程序和例4-2类似，将采样间隔改成Ts=1.5*pi/wm , 滤波器截⽌频率该成wc=wm=14欢迎下载。

￥
5.9
百度文库VIP限时优惠现在开通,立享6亿+VIP内容
立即获取
matlab对信号抽样,matlab信号抽样与恢复
matlab对信号抽样,matlab信号抽样与恢复

1、实验⼀ 信号抽样与恢复⼀、实验⽬的学会⽤MATLAB实现连续信号的采样和重建⼆、实验原理1抽样定理若是带限信号，带宽为, 经采样后的频谱就是将的频谱 在频率轴上以采样频率为间隔进⾏周期延拓。因此，当时，不会发⽣频率混叠；⽽当 < 时将发⽣频率混叠。2信号重建经采样后得到信号经理想低通则可得到重建信号，即：=*其中：=所以：=*=*=上式表明，连续信号可以展开成抽样函数的⽆穷级数。利⽤MATLAB中的来表⽰，有 ，所以可以得到在MATLAB中信号由重建的表达式如下：=我们选取信号=作为被采样信号，当采样频率=2时，称为临界采样。我们取理想低通的截⽌频率=。下⾯程序实现对信号=的采样及由该采样信号 参考技术A 一 信号抽样与恢复

一、实验目的

学会用MA TLAB 实现连续信号的采样与重建

二、实验原理

1.抽样定理

若)(t f 就是带限信号,带宽为m ω, )(t f 经采样后的频谱)(ωs F 就就是将)(t f 的频谱 )(ωF 在频率轴上以采样频率s ω为间隔进行周期延拓。因此,当s ω≥m ω时,不会发生频率混叠;而当 s ω

2.信号重建

经采样后得到信号)(t f s 经理想低通)(t h 则可得到重建信号)(t f ,即:

)(t f =)(t f s *)(t h

其中:)(t f s =)(t f ∑∞∞--)(s nT t δ=∑∞

∞--)()(s

s nT t nT f δ )()(t Sa T t h c c s ωπ

ω= 所以:

)(t f =)(t f s *)(t h =∑∞∞--)()(s s nT t nT f δ*)(t Sa T c c s

ωπ

ω =πωc s T ∑∞∞--)]([)(s c s

nT t Sa nT f ω

上式表明,连续信号可以展开成抽样函数的无穷级数。

利用MA TLAB 中的t t t c ππ)sin()(sin =来表示)(t Sa ,有 )(sin )(π

t c t Sa =,所以可以得到在MATLAB 中信号由)(s nT f 重建)(t f 的表达式如下:

)(t f =πωc s T ∑∞∞--)]([sin )(s c s nT t c nT f π

ω 我们选取信号)(t f =)(t Sa 作为被采样信号,当采样频率s ω=2m ω时,称为临界采样。我们取理想低通的截止频率c ω=m ω。下面程序实现对信号)(t f =)(t Sa 的采样及由该采样信

定时误差估计与恢复

在数字通信系统中，由于发送端的时钟和接收端的时钟来自于不同的本地振荡器，二者之间不完全同步，同时信号传输过程中存在延迟问题，导致接收端无法在每个符号的最优判决点上采样。以及由于带通滤波器的存在使得信号有一部分失真，这将会降低采样点数据的信噪比，同时也会带来码间干扰，增大信号解调的误码率，恶化通信系统的性能。
在所有的无线通信系统中，接收机不仅必须将时钟频率恢复到与接收的数字信号保持一致，还需要确定每个符号间隔内的采样位置，这取决于恢复的定时相位，定时相位就是在每一个符号间隔 内选取的采样时刻。事实上，由于通信双方采用的时钟之间存在时钟漂移，所以必须实时调整接收机恢复时钟的时钟频率和定时相位来补偿时钟漂移，以确保输出信号的最佳采样。传统的接收机通过反馈的方式去控制本地采样时钟晶体振荡器来进行相位的调整以实现定时同步，但是在全数字接收机内，由于A/D转换器的采样时钟频率固定不变，无法直接得到每个符号的最佳采样值，因此需要对接收信号的采样值进行插值运算才能获得每个符号的最佳采样值，所以插值滤波器将在全数字接收机的定时同步过程中发挥重要的作用。
可参考插值法位同步 gardner算法
定时误差估计


内插滤波
定时同步完成了对接收信号中每个符号的最优判决点的输出，本质上实现了数据速率的转换，将数据速率由采样率转变为了符号速率。在信号处理中通常采用内插技术来实现信号速率的转换。在定时同步过程中，内插滤波器的作用就是通过对尚未同步的采样数据进行插值处理来得出每个符号最优判决时刻的数值。内插滤波器的基本原理就是通过采样得到的离散信号恢复出原始连续信号之后再进行重采样，从而得到最佳采样判决时刻的值。

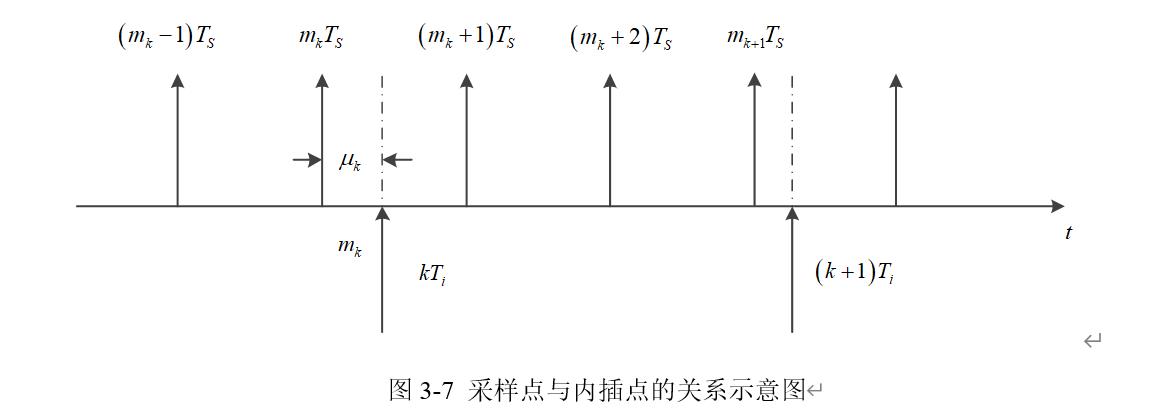
四个点得到一个插值点，刚好将数据速率恢复为符号速率。
虽然原理上内插滤波需要先重构出原始的连续信号再进行重采样，但是在实际应用中并不需重构原始信号，而是采用数据拟合的方式利用实际采样数据计算出每个符号最优判决时刻的估计值。

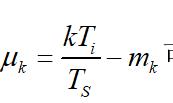
uk=(index_k+err)*K-index_mk;