密码学基础
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了密码学基础相关的知识,希望对你有一定的参考价值。
参考技术A 密码学是研究如何保护信息安全性的一门科学,涉及数学、物理、计算机、信息论、编码学、通讯技术等学科,已经在生活中得到广泛应用。 密码学组成分支分为编码学和密码分析学。密码编码学主要研究对信息进行编码,实现信息的隐蔽。密码分析学主要研究加密消息的破译或消息的伪造。二者相互独立,又相互依存,在矛盾与斗争中发展,对立统一。
密码学的发展历史大致可划分为三个阶段:
机密性
仅有发送方和指定的接收方能够理解传输的报文内容。窃听者可以截取到加密了的报文,但不能还原出原来的信息,即不能得到报文内容。
鉴别
发送方和接收方都应该能证实通信过程所涉及的另一方, 通信的另一方确实具有他们所声称的身份。即第三者不能冒充跟你通信的对方,能对对方的身份进行鉴别。
报文完整性
即使发送方和接收方可以互相鉴别对方,但他们还需要确保其通信的内容在传输过程中未被改变。
不可否认性
如果人们收到通信对方的报文后,还要证实报文确实来自所宣称的发送方,发送方也不能在发送报文以后否认自己发送过报文。
密码体制是一个使通信双方能进行秘密通信的协议。密码体制由五要素组成,P(Plaintext明文集合),C(Ciphertext密文集合),K(Key密钥集合),E(Encryption加密算法),D(Decryption解密算法),且满足如下特性:
<script type="math/tex; mode=display" id="MathJax-Element-1"> p ∈ P </script>
<script type="math/tex; mode=display" id="MathJax-Element-2"> c ∈ C </script>
<script type="math/tex; mode=display" id="MathJax-Element-3"> k1 ∈ K, k2 ∈ K </script>
<script type="math/tex; mode=display" id="MathJax-Element-6"> E_k1(p) = c,D_k2(c) = p </script>
无论是用手工或机械完成的古典密码体制,还是采用计算机软件方式或电子电路的硬件方式完成的现代密码体制,其加解密基本原理都是一致的。都是基于对明文信息的替代或置换,或者是通过两者的结合运用完成的。
替代(substitution cipher):有系统地将一组字母换成其他字母或符号;
例如‘help me’变成‘ifmq nf’(每个字母用下一个字母取代)。
置换(Transposition cipher):不改变字母,将字母顺序重新排列;
例如‘help me’变成‘ehpl em’(两两调换位置)。
密码分析者通常利用以下几种方法对密码体制进行攻击:
已知明文分析法:
知道一部分明文和其对应的密文,分析发现秘钥。
选定明文分析法:
设法让对手加密自己选定的一段明文,并获得对应的密文,在此基础上分析发现密钥。
差别比较分析法:
设法让对方加密一组差别细微的明文,通过比较他们加密后的结果来分析秘钥。
无条件安全:
无论破译者的计算能力有多强,无论截获多少密文,都无法破译明文。
计算上安全:
破译的代价超出信息本身的价值,破译所需的时间超出信息的有效期。
任何密码系统的应用都需要在安全性和运行效率之间做出平衡,密码算法只要达到计算安全要求就具备了实用条件,并不需要实现理论上的绝对安全。1945年美国数学家克劳德·E·香农在其发布的《密码学的数学原理》中,严谨地证明了一次性密码本或者称为“弗纳姆密码”(Vernam)具有无条件安全性。但这种绝对安全的加密方式在实际操作中需要消耗大量资源,不具备大规模使用的可行性。事实上,当前得到广泛应用的密码系统都只具有计算安全性。
一个好的密码体制应该满足以下两个条件:
在已知明文和密钥的情况下,根据加密算法计算密文是容易的;在已知密文和解密密钥的情况下,计算明文是容易的。
在不知道解密密钥的情况下,无法从密文计算出明文,或者从密文计算出明文的代价超出了信息本身的价值。
常见的密码算法包括:
对称密码体制也称单钥或私钥密码体制,其加密密钥和解密密钥相同,或实质上等同, 即从一个易于推出另一个。
优点:保密性高,加密速度快,适合加密大量数据,易于通过硬件实现;
缺点:秘钥必须通过安全可靠的途径传输,秘钥的分发是保证安全的关键因素;
常见对称密码算法:DES (密钥长度=56位)、3DES( 三个不同的密钥,每个长度56位)、AES(密钥长度128/192/256可选)、IDEA(密钥长度128位)、RC5(密钥长度可变)。
根据加密方式的不同,对称密码又可以分为分组密码和序列密码。
将明文分为固定长度的组,用同一秘钥和算法对每一块加密,输出也是固定长度的密文,解密过程也一样。
又称为流密码,每次加密一位或一字节的明文,通过伪随机数发生器产生性能优良的伪随机序列(密钥流),用该序列加密明文消息序列,得到密文序列,解密过程也一样。
非对称密码体制又称双钥或公钥密码体制,其加密密钥和解密密钥不同,从一个很难推出另一个。其中的加密密钥可以公开,称为公开密钥,简称公钥;解密密钥必须保密,称为私有密钥,简称私钥。
优点:密钥交换可通过公开信道进行,无需保密。既可用于加密也可用于签名。
缺点:加密速度不如对称密码,不适合大量数据加密,加密操作难以通过硬件实现。
非对称密码体制不但赋予了通信的保密性,还提供了消息的认证性,无需实现交换秘钥就可通过不安全信道安全地传递信息,简化了密钥管理的工作量,适应了通信网的需要,为保密学技术应用于商业领域开辟了广阔的前景。
常见的非对称密码算法:RSA(基于大整数质因子分解难题)、ECC(基于椭圆曲线离散对数难题)。
对非对称密码的误解
非对称密码比对称密码更安全?
任何一种算法的安全都依赖于秘钥的长度、破译密码的工作量,从抗分析的角度看,没有哪一方更优越;
非对称密码使对称密码成为过时技术?
公钥算法很慢,一般用于密钥管理和数字签名,对称密码将长期存在,实际工程中采用对称密码与非对称密码相结合。
哈希函数将任意长的消息映射为一个固定长度的散列值,也称消息摘要。消息摘要可以作为认证符,完成消息认证。
哈希是单向函数,从消息摘要来推理原消息是极为困难的。哈希函数的安全性是由发生碰撞的概率决定的。如果攻击者能轻易构造出两个不同的消息具有相同的消息摘要,那么这样的哈希函数是不可靠的。
常见的哈希函数有:MD5,SHA1,HMAC。
数字签名是公钥密码的典型应用,可以提供和现实中亲笔签名相似的效果,在技术上和法律上都有保证。是网络环境中提供消息完整性,确认身份,保证消息来源(抗抵赖性)的重要技术。
数字签名与验证过程:
发送方用哈希函数从报文文本中生成一个128位的散列值(或报文摘要),发送方用自己的私钥对这个散列值进行加密来形成自己的数字签名。然后,这个数字签名将作为报文的附件和报文一起发送给接收方。接收方收到报文后,用同样的哈希函数从原始报文中计算出散列值(或报文摘要),接着再用发送方的公钥来对报文附加的数字签名进行解密得出另一个散列值,如果两个散列值相同,那么接收方就能确认该数字签名是发送方的。通过数字签名能够实现消息的完整性和不可抵赖性。
在网络安全中,密钥的地位举足轻重
。如何安全可靠、迅速高效地分配密钥、管理密钥一直是密码学领域中的重要问题。
密钥生成可以通过在线或离线的交互协商方式实现,如密码协议等 。密钥长度应该足够长。一般来说,密钥长度越大,对应的密钥空间就越大,攻击者使用穷举猜测密码的难度就越大。选择密钥时,应该避免选择弱密钥,大部分密钥生成算法采用随机过程或伪随机过程生成密钥。
采用对称加密算法进行保密通信,需要共享同一密钥。通常是系统中的一个成员先选择一个秘密密钥,然后将它传送另一个成员或别的成员。X9.17标准描述了两种密钥:密钥加密密钥和数据密钥。密钥加密密钥加密其它需要分发的密钥;而数据密钥只对信息流进行加密。密钥加密密钥一般通过手工分发。为增强保密性,也可以将密钥分成许多不同的部分然后用不同的信道发送出去。
密钥附着一些检错和纠错位来传输,当密钥在传输中发生错误时,能很容易地被检查出来,并且如果需要,密钥可被重传。接收端也可以验证接收的密钥是否正确。发送方用密钥加密一个常量,然后把密文的前2-4字节与密钥一起发送。在接收端,做同样的工作,如果接收端解密后的常数能与发端常数匹配,则传输无错。
当密钥需要频繁的改变时,频繁进行新的密钥分发的确是困难的事,一种更容易的解决办法是从旧的密钥中产生新的密钥,有时称为密钥更新。可以使用单向函数进行更新密钥。如果双方共享同一密钥,并用同一个单向函数进行操作,就会得到相同的结果。
密钥可以存储在脑子、磁条卡、智能卡中。也可以把密钥平分成两部分,一半存入终端一半存入ROM密钥。还可采用类似于密钥加密密钥的方法对难以记忆的密钥进行加密保存。
密钥的备份可以采用密钥托管、秘密分割、秘密共享等方式。
密钥托管:
密钥托管要求所有用户将自己的密钥交给密钥托管中心,由密钥托管中心备份保管密钥(如锁在某个地方的保险柜里或用主密钥对它们进行加密保存),一旦用户的密钥丢失(如用户遗忘了密钥或用户意外死亡),按照一定的规章制度,可从密钥托管中心索取该用户的密钥。另一个备份方案是用智能卡作为临时密钥托管。如Alice把密钥存入智能卡,当Alice不在时就把它交给Bob,Bob可以利用该卡进行Alice的工作,当Alice回来后,Bob交还该卡,由于密钥存放在卡中,所以Bob不知道密钥是什么。
秘密分割:
秘密分割把秘密分割成许多碎片,每一片本身并不代表什么,但把这些碎片放到一块,秘密就会重现出来。
秘密共享:
将密钥K分成n块,每部分叫做它的“影子”,知道任意m个或更多的块就能够计算出密钥K,知道任意m-1个或更少的块都不能够计算出密钥K。秘密共享解决了两个问题:一是若密钥偶然或有意地被暴露,整个系统就易受攻击;二是若密钥丢失或损坏,系统中的所有信息就不能用了。
加密密钥不能无限期使用,有以下有几个原因:密钥使用时间越长,它泄露的机会就越大;如果密钥已泄露,那么密钥使用越久,损失就越大;密钥使用越久,人们花费精力破译它的诱惑力就越大——甚至采用穷举攻击法。
不同密钥应有不同有效期。数据密钥的有效期主要依赖数据的价值和给定时间里加密数据的数量。价值与数据传送率越大所用的密钥更换越频繁。如密钥加密密钥无需频繁更换,因为它们只是偶尔地用作密钥交换,密钥加密密钥要么被记忆下来,要么保存在一个安全地点,丢失该密钥意味着丢失所有的文件加密密钥。
公开密钥密码应用中的私钥的有效期是根据应用的不同而变化的。用作数字签名和身份识别的私钥必须持续数年(甚至终身),用作抛掷硬币协议的私钥在协议完成之后就应该立即销毁。即使期望密钥的安全性持续终身,两年更换一次密钥也是要考虑的。旧密钥仍需保密,以防用户需要验证从前的签名。但是新密钥将用作新文件签名,以减少密码分析者所能攻击的签名文件数目。
如果密钥必须替换,旧钥就必须销毁,密钥必须物理地销毁。
PKI是一个利用公钥加密技术为密钥和证书的管理,所设计的组件、功能子系统、操作规程等的集合,它的主要任务是管理密钥和证书,为网络用户建立安全通信信任机制。
数字证书是一个包含用户身份信息、公钥信息、证书认证中心(CA)数字签名的文件。
作用:数字证书是各类终端实体和最终用户在网上进行信息交流及商业活动的身份证明,在电子交易的各个缓解,交易的各方都需要验证对方数字证书的有效性,从而解决相互间的信任问题。
CA全称Certificate Authentication,是具备权威性的数字证书申请及签发机构。
CA作为PKI的核心部分,主要由注册服务器组、证书申请受理和审核机构、认证中心服务器三者组成。
注册服务器:通过 Web Server 建立的站点,可为客户提供24×7 不间断的服务。客户在网上提出证书申请和填写相应的证书申请表。
证书申请受理和审核机构:负责证书的申请和审核。
认证中心服务器:是数字证书生成、发放的运行实体,同时提供发放证书的管理、证书废止列表(CRL)的生成和处理等服务。
通过CA可以实现以下功能:
1. 接收验证最终用户数字证书的申请;
2. 确定是否接受最终用户数字证书的申请和审批;
3. 向申请者颁发、拒绝颁发数字证书;
4. 接收、处理最终用户数字证书的更新;
5. 接受最终用户数字证书的查询、撤销;
6. 产生和发布CRL(证书废止列表);
7. 数字证书的归档;
8. 密钥归档;
9. 历史数据归档;
五、量子密码
5.1 量子计算
由于量子计算技术取得了出人意料的快速发展,大量仅能抵御经典计算机暴力破解的密码算法面临被提前淘汰的困境 。
非对称密码系统有效解决了对称密码面临的安全密钥交换问题,因而广泛应用于公钥基础设施、数字签名、联合授权、公共信道密钥交换、安全电子邮件、虚拟专用网以及安全套接层等大量网络通信活动之中。不幸的是,随着量子计算的发展,包括RSA密码、ECC密码以及DH密钥交换技术等非对称密码算法已经从理论上被证明彻底丧失了安全性。相对于对称密码系统还可以采取升级措施应对量子威胁,非对称密码系统必须采取全新方法进行重建 。
5.2 量子密码
量子密码是以量子力学和密码学为基础,利用量子物理学中的原理实现密码体制的一种新型密码体制,与当前大多使用的经典密码体制不一样的是,量子密码利用信息载体的物理属性实现。目前量子密码用于承载信息的载体包括光子、压缩态光信号、相干态光信号等。
由于量子密码体制的理论基础是量子物理定理,而物理定理是物理学家经过多年的研究与论证得出的结论,有可靠的理论依据,且不论在何时都是不会改变的,因此,理论上,依赖于这些物理定理的量子密码也是不可攻破的,量子密码体制是一种无条件安全的密码体制。
密码学基础:Pedersen Commitment
介绍
Pederson承诺是密码学中承诺的一种,1992年被Torben Pryds Pedersen在“Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing”一文中提出。
目前Pedersen Commitment主要搭配椭圆曲线密码学使用(当然也可以结合指数运算)。具有基于离散对数困难问题的强绑定性和同态加法特性的密文形式。
以结合椭圆曲线为例来说明,Pedersen承诺核心公式表达:
C = r * G + v * H
上述公式中,C为生成的承诺值,G、H为特定椭圆曲线上的生成点,r代表着盲因子(Blinding factor),v则代表着原始信息。由于G、H为特定椭圆曲线上的生成点,所以r * G、v * H可以看作是相应曲线上的公钥(r、v同理也可以视为私钥)。
承诺生成和揭露过程如图:
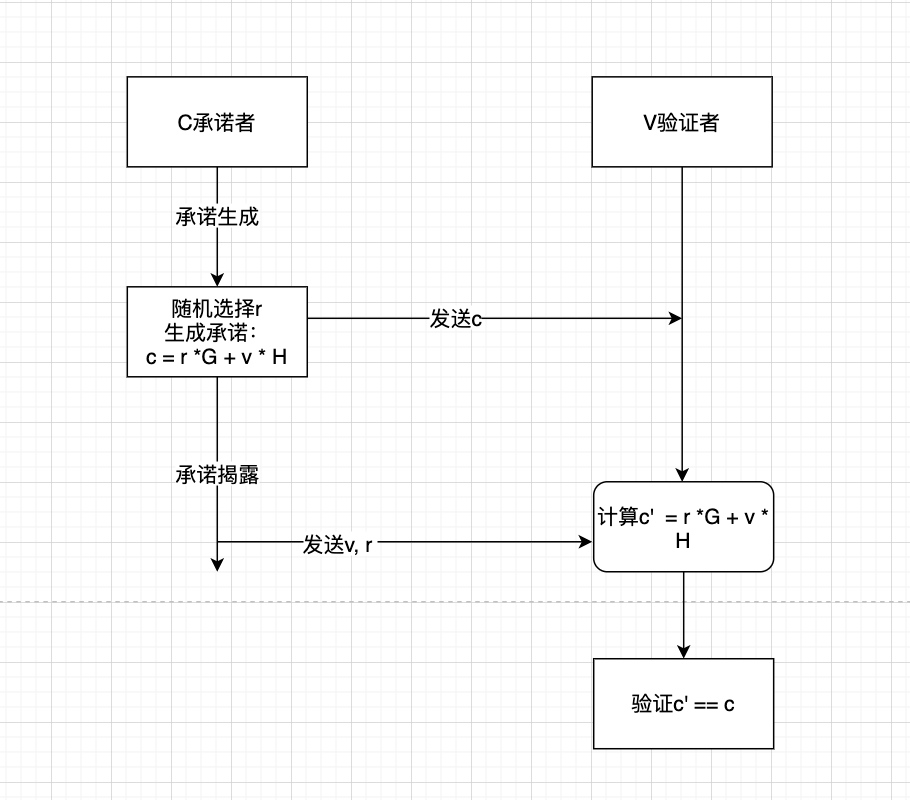
由于引入了随机盲因子r,对于同一个v会就能产生不同的承诺c,即便敏感隐私数据v不变,最终的承诺c也会随着r的变化而变化,因此提供了信息论安全的隐匿性。这一点类似ECDSA,Schnorr签名采用的手法。
Pedersen承诺加法同态
Pedersen承诺还具有加法同态特性。所谓加法同态,即两数相加和的密文等于两数的密文相加!假设明文a, b ,加密函数e,满足:
c = a + b
e(a) + e (b) = e(c)
Pedersen承诺结合椭圆曲线天然地具备了加法同态的特性,这是椭圆曲线点运算的性质决定的。
假设有两个要承诺的信息v1,v2, 随机数r1,r2,生成对应的两个承诺:
C(v1)=r1∗G+v1∗H
C(v2)=r2∗G+v2∗H
则v1+v2承诺结果:
C(v1+v2)=(r1+r2)G+(v1+v2)∗H
(r1G+v1∗H)+(r2∗G+v2∗H)
C(v1)+C(v2)
Pedersen承诺还可以扩展构造v1∗v2等复杂的情况,来证明新产生的承诺满足与原始承诺之间存在指定的约束关系。
小结
Pedersen承诺产生方式,有些类似加密,签名之类的算法。但是,作为密码学承诺重在“承诺”,并不提供解密算法,即如果只有r,无法有效地计算出隐私数据v。
目前Pedersen承诺在区块链中的应用主要在隐私币中,如zcash,MimbleWimble,Monero等。
以上是关于密码学基础的主要内容,如果未能解决你的问题,请参考以下文章