具体数学的内容简介

Posted 2023-04-27

参考技术A

《具体数学:计算机科学基础:第2版》是一本在大学中广泛使用的经典数学教科书．书中讲解了许多计算机科学中用到的数学知识及技巧，教你如何把一个实际问题一步步演化为数学模型，然后通过计算机解决它，特别着墨于算法分析方面．其主要内容涉及和式、整值函数、数论、二项式系数、特殊的数、生成函数、离散概率、渐近式等，都是编程所必备的知识．另外，本书包括了六大类500 多道习题，并给出了所有习题的解答，有助读者加深书中内容的理解．　　《具体数学:计算机科学基础:第2版》面向从事计算机科学、计算数学、计算技术诸方面工作的人员，以及高等院校相关专业的师生．
原书英文简介
This book introduces the mathematics that supports advanced computer Programming and the analysis of algorithms. The primary aim of its well-known authors is to provide a solid and relevant base of mathematical skills--the skills needed to solve complex problems, to evaluate horrendous sums, and to discover subtle Patterns in data. It is an indispensable text and reference not only for computer scientists--the authors themselves rely heavily on it! but for serious users Of mathematics in virtually every discipline. Concrete mathematics is a blending of continuous and disCRETE mathematics: More concretely, the authors explain, it is the controlled manipulation of mathematical formulas,using a collection of techniques for solving problems. The subject mater is primarily an expansion of the Mathematical Preliminaries section in Knuth's c1assic Art of Computer Programming, but the style of presentation is more leisurely, and individual topics are covered more deeply. Several new topics have been added, and the most significant ideas have been traced to their historical roots. The book includes more than 500 exercises, divided into six categories. Complete answers are provided for all exercises, except research problems, making the book particularly valuable for self-study.

数学建模暑期集训1：模糊数学基础

在数学建模中，有一种评价类的方法叫做模糊综合评价法。本篇内容就主要记录一些模糊数学的基础，下篇内容将具体记录这种方法。由于模糊数学是研究生课程内容，文中自己的主观理解可能会有偏差，如有错误，可请指出。

文章目录

• 1.模糊概念
• • 1.1秃头悖论
  • 1.2模糊概念
• 2.经典集合与特征函数
• 3.模糊集合与隶属函数
• 4.经典集合与模糊集合的关系
• 5.模糊集合的分类
• 6.模糊集合的运算
• 7.$\lambda$-截集
• 8.普通关系与二元关系
• 9.模糊关系的合成
• 10.模糊等价关系
• 11.经典等价关系
• 12.模糊相似关系
• 13.模糊聚类
• 14.数据标准化
• 15.模糊相似矩阵建立方法

1.模糊概念

1.1秃头悖论

什么是秃头？
掉一根头发，不是秃头；
再掉一根头发，不是秃头；
…
掉最后一根头发，也不是秃头；
这种反常识的推论就是秃头悖论。

1.2模糊概念

和秃头一样，许多概念没有被精确量化，比如，掉多少头发算秃头。
同样，成绩好、年轻、肥胖也均是模糊概念。

2.经典集合与特征函数

经典集合特点：确定性、互斥性

3.模糊集合与隶属函数

模糊集合特点：非此即彼

隶属度：属于[0,1]区间，越大表示越属于这种集合。

隶属集合三种表示方法：

注：这里的除号和加号不具有计算意义，仅是用作标记。

4.经典集合与模糊集合的关系

当A(x) = 0.5时，点x最具模糊性；
映射A(x)只取0或1时，模糊子集A就是经典子集，而A(x)就是它的特征函数. 可见经典子集就是模糊子集的特殊情形。

5.模糊集合的分类

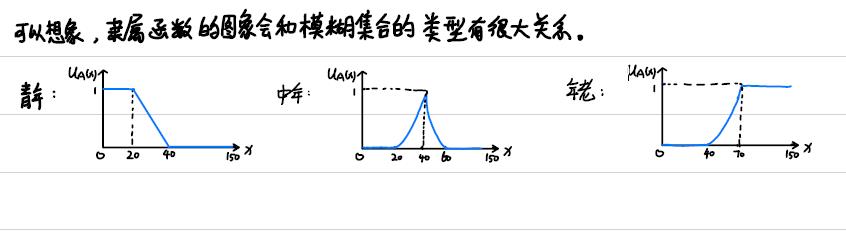
6.模糊集合的运算

7.$\lambda$-截集

8.普通关系与二元关系

9.模糊关系的合成

注：模糊矩阵相乘遵循一般矩阵相乘的规则，原本的乘法变取小，原本的加法变取大。
看个例子：

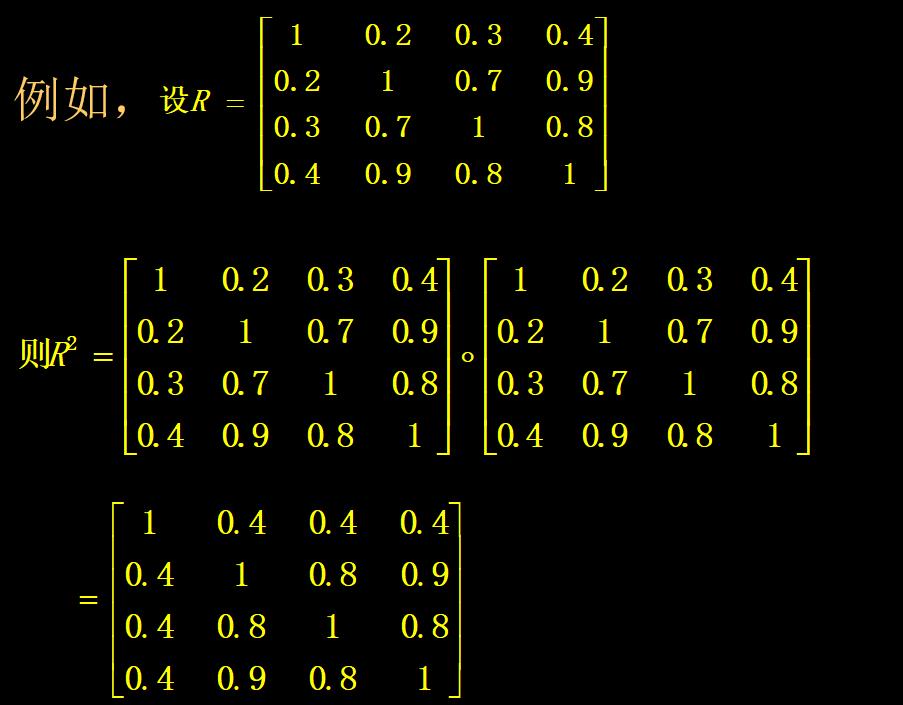
10.模糊等价关系

11.经典等价关系

模糊等价关系是经典等价关系的推广

两者联系：R是模糊等价关系当且经当R的任意$\lambda$-截集都是经典等价关系。

12.模糊相似关系

模糊相似关系未必是模糊等价关系

13.模糊聚类

1、得到模糊相似关系
2、由模糊相似关系出发得到模糊等价关系
3、由模糊等价关系的$\lambda$-截集得到等价关系，从而分类

14.数据标准化

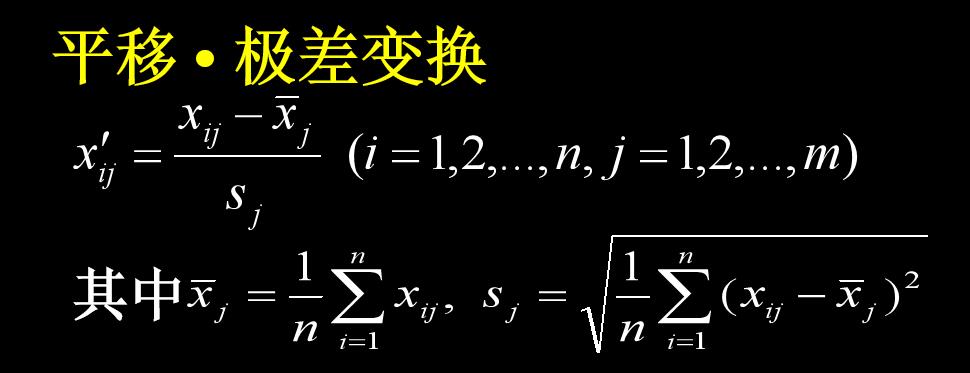
15.模糊相似矩阵建立方法

实际上，模糊综合评价方法并非上述那么多的知识，主要掌握隶属函数的意义即可。