c++高手进 float 精度问题，这个要是丢失精度的话应该小才对？为啥变大了？

Posted 2023-04-25

#include<iostream>
#include<cstdio>
using namespace std;
int main()

float n=0.15;
printf("%.15lf\n",n);
return 0;

/*
output
0.150000005960464!!!!!!!
*/

32bi浮点只有约6个(不到7个)十进制有效数字..
而%.15lf设了小数点后15个数位的精度，有多余输出。
所以0.(150000)005960464中只有括号部分是精确的，其余的数值可以舍去， 参考技术A 我猜后面的可能是内存里的东西，直接被读出来了，跟你的程序半毛钱关系都没有吧。 参考技术B 因为%.15lf的意思是格式化输出小数点後15位，因此有了你现在的结果 参考技术C float应该用%f输出，而且你要输出的位数大于他的精度，所以后面是随机值，跟大小没关系 参考技术D float的有效精度好像只有6位的，再多了就没意义了，变大变小也就没有意义了

java float double精度为啥会丢失

由于对float或double 的使用不当，可能会出现精度丢失的问题。问题大概情况可以通过如下代码理解:

public class FloatDoubleTest   
public static void main(String[] args)   
float f = 20014999;  
double d = f;  
double d2 = 20014999;  
System.out.println("f=" + f);  
System.out.println("d=" + d);  
System.out.println("d2=" + d2);  
  

得到的结果如下：

f=2.0015E7
d=2.0015E7
d2=2.0014999E7

从输出结果可以看出double 可以正确的表示20014999 ，而float 没有办法表示20014999 ，得到的只是一个近似值。这样的结果很让人讶异。20014999 这么小的数字在float下没办法表示。于是带着这个问 题，做了一次关于float和double学习，做个简单分享，希望有助于大家对java 浮 点数的理解。

 

关于 java 的 float 和 double

Java 语言支持两种基本的浮点类型： float 和 double 。java 的浮点类型都依据 IEEE 754 标准。IEEE 754 定义了32 位和 64 位双精度两种浮点二进制小数标准。

IEEE 754 用科学记数法以底数为 2 的小数来表示浮点数。32 位浮点数用 1 位表示数字的符号，用 8 位来表示指数，用 23 位来表示尾数，即小数部分。作为有符号整数的指数可以有正负之分。小数部分用二进制（底数 2 ）小数来表示。对于64 位双精度浮点数，用 1 位表示数字的符号，用 11 位表示指数，52 位表示尾数。如下两个图来表示：

float(32位):

double(64位):

都是分为三个部分：

(1) 一 个单独的符号位s 直接编码符号s 。

(2)k 位 的幂指数E ，移 码表示 。

(3)n 位 的小数，原码表示 。

那么 20014999 为什么用 float 没有办法正确表示？

结合float和double的表示方法，通过分析 20014999 的二进制表示就可以知道答案了。

以下程序可以得出 20014999 在 double 和 float 下的二进制表示方式。

public class FloatDoubleTest3   
public static void main(String[] args)   
double d = 8;  
long l = Double.doubleToLongBits(d);  
System.out.println(Long.toBinaryString(l));  
float f = 8;  
int i = Float.floatToIntBits(f);  
System.out.println(Integer.toBinaryString(i));  
  

输出结果如下：

Double:100000101110011000101100111100101110000000000000000000000000000
Float:1001011100110001011001111001100

对于输出结果分析如下。对于都不 double 的二进制左边补上符号位 0 刚好可以得到 64 位的二进制数。根据double的表 示法，分为符号数、幂指数和尾数三个部分如下：

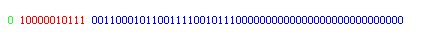
对于 float 左边补上符 号位 0 刚好可以得到 32 位的二进制数。 根据float的表示法， 也分为 符号数、幂指数和尾数三个部分如下：

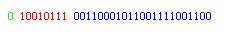
绿色部分是符号位，红色部分是幂指数，蓝色部分是尾数。

对比可以得出:符号位都是 0 ，幂指数为移码表示,两者刚好也相等。唯一不同的是尾数。

在 double 的尾数 为： 001100010110011110010111 0000000000000000000000000000 ，省略后面的零，至少需要24位才能正确表示 。

而在 float 下面尾数 为： 00110001011001111001100 ，共 23 位。

为什么会这样？原因很明显，因为 float尾数 最多只能表示 23 位，所以 24 位的 001100010110011110010111 在 float 下面经过四舍五入变成了 23 位的 00110001011001111001100 。所以 20014999 在 float 下面变成了 20015000 。

也就是说 20014999 虽然是在float的表示范围之内，但 在 IEEE 754 的 float 表示法精度长度没有办法表示出 20014999 ，而只能通过四舍五入得到一个近似值。

 

总结：

浮点运算很少是精确的，只要是超过精度能表示的范围就会产生误差。往往产生误差不是 因为数的大小，而是因为数的精度。因此，产生的结果接近但不等于想要的结果。尤其在使用 float 和 double 作精确运 算的时候要特别小心。

可以考虑采用一些替代方案来实现。如通过 String 结合 BigDecimal 或 者通过使用 long 类型来转换。

参考技术A 　　首先有一个观念，在计算机里所有的数据都是以二进制的形势保存的。
　　我们来简单的举个例子,
　　对于int类型的数值我们不陌生, 10进制类型和2进制的转换也很简单
　　比如9= 0000 1001, 22=0001 0110 等
　　（注意：以下x^y 表示x的y次方）
　　换一种表示方式 9 = 2^3+2^0，22=2^4+2^2+2^1.很简单对不对

　　但是对于float和double类型的数据就变得不一样了，在清楚为什么精度会丢失的问题之前还需要先明白一件事
　　就像在10进制里 0.1 = 10^-1 0.01=10^-2 一样 在2进制里 小数点后边的数字也是用2^-n次方来解决的.
　　那么问题来了,大家都知道 2^-1 =0.5,2^-2=0.25
　　如果你想表示0.6的话在10进制里可以简单的用6*10^-1次方来表示,但是在2进制里怎么表示呢,？只能用尽可能接近的数据来表示比如 (1*2^-1)+(1*2^-3) 也就是 0.5+0.125 =0.625 约等于0.6 （这里只是举个例子,实际计算机在存储的时候要复杂一些）,因为在2进制里边没有“准确”表示 比如 0.1，0.00000001 这样数据的2进制数据.
　　还有一点,操作系统的位数也会影响到float和double的精度,比如32位和64位

　　（纯手打 不明白的话 追问）