C语言根据层次遍历和中序遍历求二叉树的前序遍历和后序遍历。下面有我的建树函数，有注释的。

Posted 2023-04-24

void BuildTree(char *level,char *inorder,pBiTree T)

int i;
int len=strlen(level); //取得层次遍历长度
int pos;
if(len==0)
return ;
char *p=strchr(inorder,level[0]);
if(p==NULL) //如果为空则抛弃第一个，跳到下一个；

char *L=(char*)malloc(sizeof(char)*len); //开辟数组
strncpy(L,level+1,len-1); //舍弃第一个
L[len-1]=0;
T->lchild=NULL;
T->rchild=NULL;
BuildTree(L,inorder,T); //调用建树函数
return ;
else
pos=p-inorder; //得到中序遍历左子树字符串长度
T->data=level[0]; //为根节点赋值
T->lchild=NULL;
T->rchild=NULL;

if(pos!=0) //左子树的递归调用

pBiTree left;
T->lchild=(pBiTree)malloc(sizeof(BiNode));
left=T->lchild;
char *left_level=(char*)malloc(sizeof(char)*len);
char *left_inor=(char*)malloc(sizeof(char)*(pos));
strncpy(left_level,level+1,len-1); //舍去层次遍历第一个
strncpy(left_inor,inorder,pos); //截取左子树字符串
left_level[len-1]=0;
left_inor[pos]=0;
BuildTree(left_level,left_inor,left);

if(pos!=len-1) //右子树的递归调用

pBiTree right;
T->rchild=(pBiTree)malloc(sizeof(BiNode));
right=T->rchild;
char *right_level=(char*)malloc(sizeof(char)*(len));
char *right_inor=(char*)malloc(sizeof(char)*(len-pos));
strncpy(right_level,level+1,len-1);
strncpy(right_inor,inorder+pos+1,len-pos-1);
right_level[len-1]=0;
right_inor[len-pos-1]=0;
BuildTree(right_level,right_inor,right);


运行结果：

2
输入：
CBA
BCA
输出：
CB燗
燘AC

输入：
BACDE
DAEBC
输出：
BAD燛C
燚EA谻B

参考技术A #include"cstdio"
#include"vector"
#include"cstring"
#include"algorithm"
using namespace std;
const int maxn =30;
struct node
int data;
node* lchild;
node* rchild;
;
int n;
int in[maxn];
bool vis[maxn]=false;
vector<int> lev;
node* create(vector<int> lev,int inl,int inr)
if(lev.size()==0) return NULL;
if(inl>inr) return NULL;
//printf("00\n");
node* root= new node;
root->data =lev[0];
int k;
for(k=inl;k<=inr;k++)
if(lev[0]==in[k])
break;

for(int j=inl;j<=k-1;j++)
vis[in[j]]=true;
vector<int> tempLeft,tempRight;//要函数体内新建
for(int i=1;i<lev.size();i++)
if(vis[lev[i]]==true)
tempLeft.push_back(lev[i]);
else
tempRight.push_back(lev[i]);

root->lchild =create(tempLeft,inl,k-1);
root->rchild =create(tempRight,k+1,inr);
return root;

void preorder(node* root)
if(root==NULL)
return;
printf("%d ",root->data);
preorder(root->lchild);
preorder(root->rchild);

int main()
scanf("%d",&n);
int x;
for(int i=0;i<n;i++)
scanf("%d",&x);
lev.push_back(x);

for(int j=0;j<n;j++)
scanf("%d",&in[j]);
node *root =create(lev,0,n-1);
preorder(root);
return 0;
参考技术B 这段代码不完整，缺少太多，另外不知你要问什么。追问

根据提供的层次遍历和中序遍历还原二叉树。

如
输入：
CBA
BCA
输出：（先序遍历和后序遍历）
CBA
BAC

以上是我根据中序遍历和层次遍历还原二叉树的代码；
我的错误输出也贴上去了。这样能明白吗？
其它代码与这段代码没有关联，只需要调用这个函数即可

追答

你这段代码的思想是什么呢？

本回答被提问者采纳

二叉树进阶题------前序遍历和中序遍历构造二叉树；中序遍历和后序遍历构造二叉树

根据前中后序历数组构建二叉树

• 一.根据一棵树的前序遍历与中序遍历构造二叉树
• • 思路
  • 代码
• 二.根据一棵树的中序遍历与后序遍历构造二叉树
• • 思路
  • 代码

一.根据一棵树的前序遍历与中序遍历构造二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

思路

首先我们可以知道通过前序遍历和中序遍历，就可以知道整个二叉树的结构了。然后自上而下的深度递归构造。

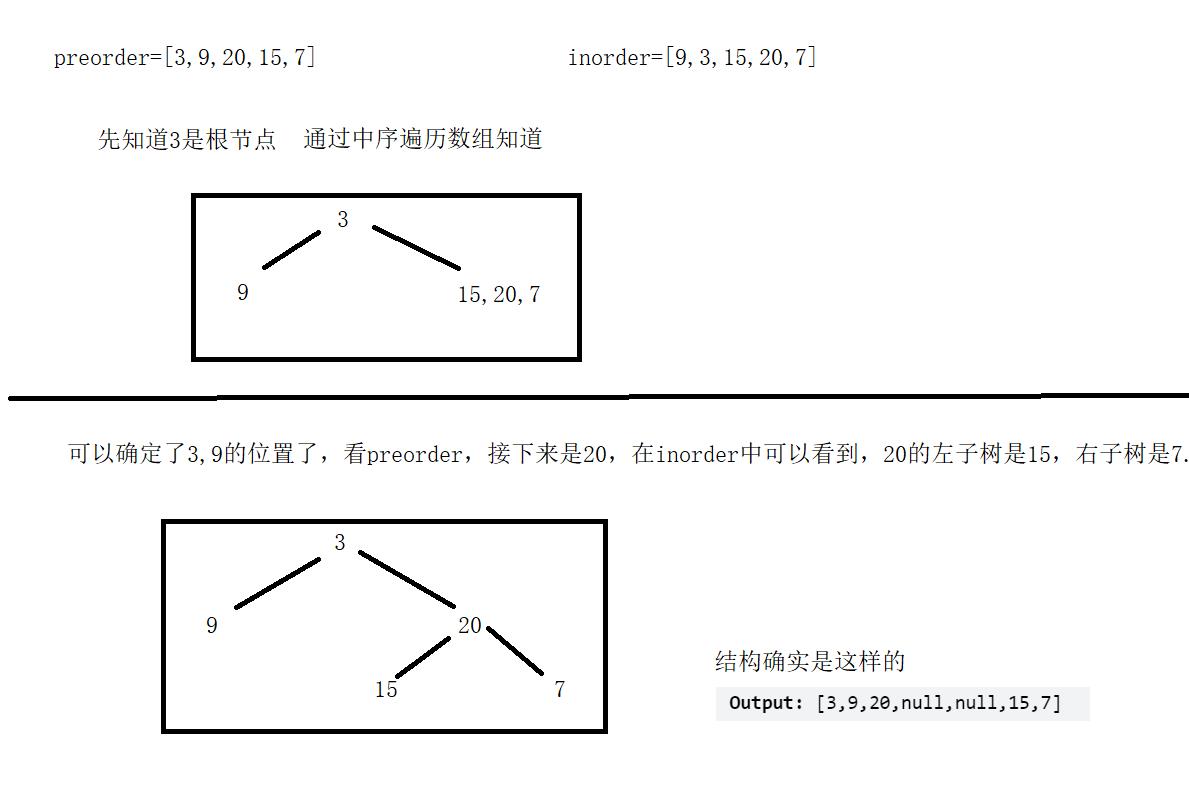
代码

private int index=0;
    public TreeNode buildTree(int[] preorder, int[] inorder) 
        index=0;
        return  buildTreeHelper(preorder,inorder,0,inorder.length);
    

    private TreeNode buildTreeHelper(int[] preorder, int[] inorder, int left, int right) 
        //空树
        if(left>=right)
            return null;
        
        //遍历完
        if(index>=preorder.length)
            return null;
        
        //根据当前根节点的值创建出根节点
        TreeNode root=new TreeNode(preorder[index]);
        index++;
        //中序遍历数组中找到root的位置
        int pos=find(inorder,left,right,root.val);
        //左子树是root在中序遍历结果中的左边的节点
        root.left=buildTreeHelper(preorder,inorder,left,pos);
        //同理，右子树是root在中序遍历结果中的右边的节点，记得要pos+1
        root.right=buildTreeHelper(preorder,inorder,pos+1,right);
        return root;
    
    
    //查找出root在中序遍历数组中的位置
    private int find(int[] inorder, int left, int right, int toFind) 
        //遍历查找
        for (int i = left; i < right; i++) 
            if(inorder[i]==toFind)
                return i;
            
        
        //没找到按理不存在（一定能找到）
        return -1;
    

二.根据一棵树的中序遍历与后序遍历构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。

思路

首先一定要先看懂我上面的前序遍历和中序遍历构造二叉树(这个理解之后，那么这题就很简单了)，看图

所以我们只需要逆置一下二叉树的后序遍历，那么就得到前序遍历的镜像了，根右左。所以就转换成了前序遍历和中序遍历二叉树的问题了。构造左右的时候只需要注意，先构造右，，再构造左即可，其余代码一模一样。

代码

private int index=0;
    public TreeNode buildTree(int[] inorder, int[] postorder) 
        index=0;
        //逆置后序遍历数组
        reverse(postorder);
        return  buildTreeHelper(postorder,inorder,0,inorder.length);
    
    //因为后序遍历，逆置一下，就是先序遍历的镜像，根右左
    //这样就转化成 先序与中序遍历构造二叉树的问题了（只是要注意左右子树顺序）
    private void reverse(int[] postorder) 
        int left=0;
        int right=postorder.length-1;
        //交换
        while (left<right)
            int tmp=postorder[left];
            postorder[left]=postorder[right];
            postorder[right]=tmp;
            left++;
            right--;
        
    

    private TreeNode buildTreeHelper(int[] postorder, int[] inorder, int left, int right) 
        //空树
        if(left>=right)
            return null;
        
        //遍历完
        if(index>=postorder.length)
            return null;
        
        //根据当前根节点的值创建出根节点
        TreeNode root=new TreeNode(postorder[index]);
        index++;
        int pos=find(inorder,left,right,root.val);
        //代码和前序遍历与中序遍历构造二叉树一样
        //只是需要注意改动一下左右构造的顺序即可
        //代码不做详细注解了，不懂的可以看前序和中序构造二叉树的代码注释(基本一模一样)
        root.right=buildTreeHelper(postorder,inorder,pos+1,right);
        root.left=buildTreeHelper(postorder,inorder,left,pos);
        return root;
    

    private int find(int[] inorder, int left, int right, int toFind) 
        for (int i = left; i < right; i++) 
            if(inorder[i]==toFind)
                return i;
            
        
        return -1;
    

有人可能会问，为啥没有前序遍历和后序遍历构造二叉树的题呢？
嘿嘿嘿，首先通过遍历构造二叉树，一定要知道两种遍历结果，并且中序遍历一定要存在，不然无法确定二叉树的结果哦。