矩阵的F-范数 的作用?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵的F-范数 的作用?相关的知识,希望对你有一定的参考价值。
F-范数 很奇怪 那个矩阵算子范数 是什么啊
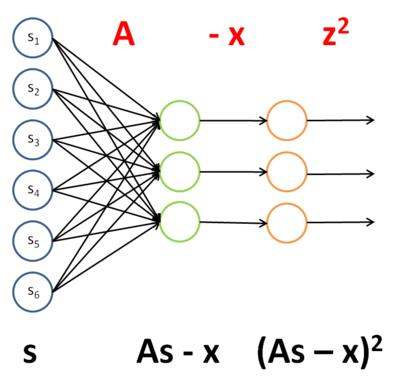
作用:F范数是把一个矩阵中每个元素的平方求和后开根号。
应用中常将有限维赋范向量空间之间的映射以矩阵的形式表现,这时映射空间上装备的范数也可以通过矩阵范数的形式表达。
矩阵范数除了正定性,齐次性和三角不等式之外,还规定其必须满足相容性:║XY║≤║X║║Y║。所以矩阵范数通常也称为相容范数。
如果║·║α是相容范数,且任何满足║·║β≤║·║α的范数║·║β都不是相容范数,那么║·║α称为极小范数。对于n阶实方阵(或复方阵)全体上的任何一个范数║·║,总存在唯一的实数k>0,使得k║·║是极小范数。
扩展资料:
如果不考虑相容性,那么矩阵范数和向量范数就没有区别,因为m*n矩阵全体和m*n维向量空间同构。引入相容性主要是为了保持矩阵作为线性算子的特征,这一点和算子范数的相容性一致,并且可以得到Mincowski定理以外的信息。
如果范数║·║满足║A║=║UAV║对任何矩阵A以及酉矩阵U,V成立,那么这个范数称为酉不变范数。
容易验证,2-范数和F-范数是酉不变范数。因为酉变换不改变矩阵的奇异值,所以由奇异值得到的范数是酉不变的,比如2-范数是最大奇异值,F-范数是所有奇异值组成的向量的2-范数。
反过来可以证明,所有的酉不变范数都和奇异值有密切联系。
参考资料来源:百度百科——矩阵范数
E-范数):║A║F= ( ∑∑ aij^2 )^1/2
(A全部元素平方和的平方根)。容易验证F-范数是相容的,但当minm,n>1时F-范数不能由向量范数诱导
(||E11+E22||F=2>1)。可以证明任一种矩阵范数总有与之相容的向量范数。例如定义 ║x║=║X║,其中X=[x,x,…,x]是
由x作为列的矩阵。由于向量的F-范数就是2-范数,所以F-范数和向量的2-范数相容。
另外还有以下结论: ║AB║F <= ║A║F ║B║2 以及 ║AB║F <= ║A║2 ║B║F
这个要具体情况具体分析 参考技术B 同求作用啊 谁给讲讲啊
F范数是把一个矩阵中每个元素的平方求和后开根号,具体作用也不清楚啊
线性代数笔记:Frobenius 范数
Frobenius 范数,简称F-范数,是一种矩阵范数,记为||·||F。
矩阵A的Frobenius范数定义为矩阵A各项元素的绝对值平方的总和开根,即
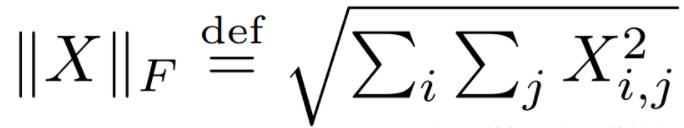
以上是关于矩阵的F-范数 的作用?的主要内容,如果未能解决你的问题,请参考以下文章