通俗理解反卷积

Posted 2023-04-17

参考技术A 卷积的原理在这里不做解释，若对于各参数都是方阵的卷积定义： i 表示输入特征矩阵的行或列，k 表示卷积核大小，s表示步长，p 表示每个维度相同的padding，则一次卷积操作之后，得到的新的特征矩阵大小为 o x o：

卷积操作本质上是一种特征抽取，数据压缩的过程，反卷积则正好相反，是一个数据扩充的过程，下面两张图片是反卷积简单示例：

反卷积也叫转置卷积，属于上采样技术范畴。

先看卷积操作的数学表达：

设有如上图三的卷积操作，i = 4, k = 2, s = 1, p = 0，x 表示输入的特征矩阵，y 表示卷积之后的输出，C 表示卷积核，定义如下：

只要好好理解一下卷积计算过程，相信对这个展开还是容易理解的。那么，y = Cx 可表示为：

所谓反卷积，其实就是上述过程的逆过程，已知（2 * 2）的 y ，想得到更大的（4 * 4）的 x ，即此时 y 是我们的输入，x 是我们的输出，x = Dy，D是反卷积过程中的采样器，和C是一样的，或者说是过滤器、权重矩阵啥的，反正就那意思。想要得到（4 * 4）的 x， 或者说（16 * 1 ）的 x， D的形状必须满足（16 * 4）,表示如下：

既然如此，D 和 C 有何关系呢？D 和 C 都是网络训练过程中的参数，参考损失反向传播理论有

深度学习—反卷积的理解

1、Deconvolution大致可以分为以下几个方面：

　　（1）非监督学习：unsupervised learning，其实就是covolutional sparse coding：这里的deconv只是观念上和传统的conv反向，传统的conv是从图片生成feature map，而deconv是用unsupervised的方法找到一组kernel和feature map，让它们重建图片。

　　（2）CNN可视化：通过deconv将CNN中conv得到的feature map还原到像素空间，以观察特定的feature map对哪些pattern的图片敏感，这里的deconv其实不是conv的可逆运算，只是conv的transpose，所以tensorflow里一般取名叫transpose_conv。

　　（3）上采样：在pixel-wise prediction比如image segmentation[4]以及image generation[5]中，由于需要做原始图片尺寸空间的预测，而卷积由于stride往往会降低图片size， 所以往往需要通过upsampling的方法来还原到原始图片尺寸，deconv就充当了一个upsampling的角色。

2、直观解释

　　反卷积就是卷积，只是中间padding了下，然后再做卷积。其实更应叫做转置卷积，只能还原原来的特征图大小，而不是原来的值。

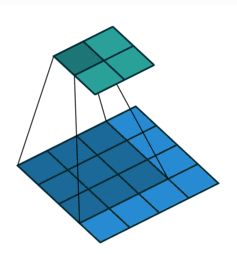
（1）卷积(convolution):卷积核为 3x3；no padding , strides=1 ；"反卷积"(the transpose of conv) 可以理解为upsample conv。卷积核为:3x3; no padding , strides=1。

   

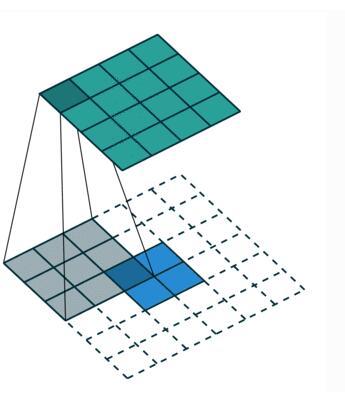
（2）那看下strides=2的时候，转置卷积相当于带洞卷积，也叫作微步卷积。

  

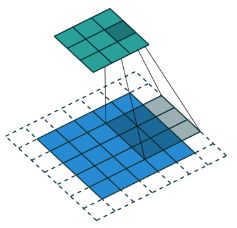
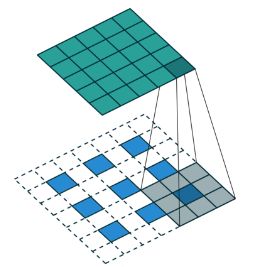
参考动图：https://github.com/vdumoulin/conv_arithmetic

3、数学解释：

　　一句话解释：逆卷积相对于卷积在神经网络结构的正向和反向传播中做相反的运算。

　　逆卷积(Deconvolution)比较容易引起误会，转置卷积(Transposed Convolution)是一个更为合适的叫法.回想第一句话，你猜的没错，所谓逆卷积其实就是正向时左乘C的转置，而反向时左乘C的转置的转置，即最终使C的运算。

　　正向传播：输入矩阵可展开为16维向量，记作想x，输出矩阵可展开为4维向量，记作y，卷积运算可表示为  y=Cx;

　　反向传播：那么当反向传播时又会如何呢？首先我们已经有从更深层的网络中得到的梯度，然后左乘C的转置的转置，做矩阵运算。

 

参考：https://www.zhihu.com/question/43609045/answer/132235276

　　　https://www.zhihu.com/question/43609045/answer/132235276