数据结构 简单算法实现在二叉排序树上查找关键值k

Posted 2023-04-17

typedef struct nodeint key; struct node *lchild; struct node *rchild;bitree; bitree *bstsearch(bitree *t, int k) if (t==0 ) return(0);else while (t!=0) if (t->key==k) return(t); else if (t->key>k) t=t->lchild; else_t=t->rchild_; 整个程序什么意思 看不懂

参考技术A 如果用C语言，应该要写成这样:
typedef
struct
nodeint
key;
struct
node
*lchild;
struct
node
*rchild;bitree;
bitree
*bstsearch(bitree
*t,
int
k)

if
(t==NULL
)
//这里t是一个指针，是不能跟0判等的，要和空指针判等

return(NULL);//如果t是空指针，表示数是空数，不存在关键值key

else

while
(t!=NULL)//要循环遍历整个树，寻找关键值key

if
(t->key==k)
//如果找到了关键值key，则返回节点指针t
return(t);
else
if
(t->key>k)
//因为是排序树，则有对于任意节点，左孩子小于根小于右孩子
t=t->lchild;
//所以如果当前节点的key大于输入值，则搜索左子树，否则右子树
else
t=t->rchild_;

return
NULL;//这里要加这个，如果搜索不到的话要返回空指针

在二叉查找树中插入节点

给定一棵二叉查找树和一个新的树节点，将节点插入到树中。

你需要保证该树仍然是一棵二叉查找树。

给出如下一棵二叉查找树，在插入节点6之后这棵二叉查找树可以是这样的：

  2             2
 / \\           / \\
1   4   -->   1   4
   /             / \\ 
  3             3   6

 

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

 

如图所示：

 

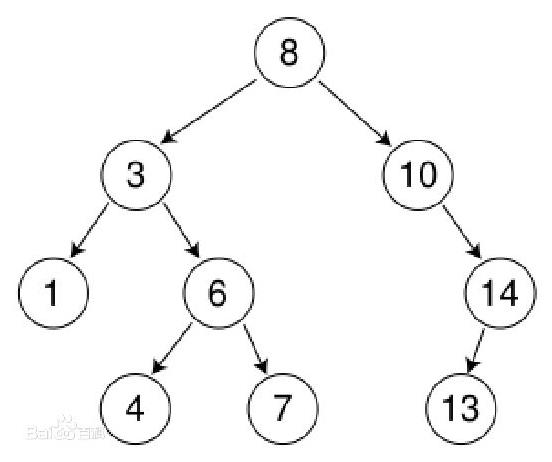
 1 <?php
 2 //二叉查找树
 3 include "show.php";//实现了一个打印的方法
 4 
 5 class tree{
 6     public $value;
 7     public $left = null;
 8     public $right = null;
 9     
10     public function __construct($value)
11     {
12         $this->value = $value;
13     }
14 }
15 
16 /**
17  * $header树的根节点
18  */
19 function add(&$header)
20 {
21     $nodes = [2, 1, 4, 3, 6];
22     foreach($nodes as $v)
23     {
24         insert_node($header, $v);
25     }
26 }
27 
28 //二叉查找树插入节点(非递归), 插入的节点均为叶子节点
29 function insert_node(&$header, $node)
30 {
31     //处理只有一个节点的情况
32     if($header == null)
33     {
34         $header = new tree($node);
35         return;
36     }
37     
38     //处理有多个节点的情况
39     $p = $header;
40     $pre = $header;
41     while($p != null)
42     {
43         $pre = $p;
44         if($node < $p->value)
45         {
46             $p = $p->left;
47         } else {
48             $p = $p->right;
49         }
50     }
51     //循环完之后，$pre即为$node的父节点
52     if($node < $pre->value)
53     {
54         $pre->left = new tree($node);
55     } else {
56         $pre->right = new tree($node);
57     }
58 }
59 
60 //二叉查找树插入节点(递归)
61 function tmp_insert_node($header, $node)
62 {
63     $tmp_node = new tree($node);
64     if($header == null)
65     {
66         $header = $tmp_node;
67         return $header;
68     }
69     
70     if($node < $header->value)
71     {
72         $header->left = tmp_insert_node($header->left, $node);
73     } else {
74         $header->right = tmp_insert_node($header->right, $node);
75     }
76     return $header;
77 }
78 
79 $header = null;
80 add($header);//非递归
81 show($header);
82 
83 $res = tmp_insert_node($header, 5);//递归
84 show($res);
85 $res = tmp_insert_node($header, 7);
86 show($res);