求多个变量的排列组合程序-C/JAVA/PHP/ASP/PYTHON均可

Posted 2023-04-16

求15个变量排列组合的算法-C/JAVA/php/ASP/PYTHON均可

格纹情况如下
有一个类似于这样的数组
CARR[]="A","B","C","D","E","F","G","H","I","J","K","L","M","N","O"

现在我想打印出所有的组合，就像
AB, ABC, ACB, ABCD, ABDC, ACBD, ACDB, ADCB, ADBC, ABCDE .......
15个的组合都要，最后写入到一个txt文件内。

随便是C JAVA PHP ASP JSP PYTHON 语言都可以
只要能输出结果就好了

成功运行加分50
各位帮忙！加油！
rrroger兄，你嵌套了很多层么？不过这东西弄了很可能还要outofmemory呢...印象中有几个算法专门用于做这个的，可惜忘了名字了，哎...

15位的排列太大了，你恐怕没有考虑到，我这个例子只给了5位的一个排列，仅供参考

import java.io.BufferedOutputStream;
import java.io.File;
import java.io.FileOutputStream;

public class Bd9Test
BufferedOutputStream buffout ;

int combine(char a[], int n, int m)
m = m > n ? n : m;

int[] order = new int[m + 1];
for (int i = 0; i <= m; i++)
order[i] = i - 1; // 注意这里order[0]=-1用来作为循环判断标识

int count = 0;
int k = m;
boolean flag = true; // 标志找到一个有效组合
while (order[0] == -1)
if (flag) // 输出符合要求的组合

StringBuffer sb = new StringBuffer();
for (int i = 1; i <= m; i++)
sb.append(a[order[i]]);

/***** 如果你不需要排列只要组合，删除这段就可以了然后打印sb.toString()****/
PermutationGenerator x = new PermutationGenerator(sb.toString().length());
StringBuffer permutation;
int[] indices;
while (x.hasMore())
permutation = new StringBuffer();
indices = x.getNext();
for (int i = 0; i < indices.length; i++)
permutation.append(sb.toString().charAt(indices[i]));

System.out.println(permutation.toString());
// try
// buffout.write((permutation.toString()+"\r\n").getBytes());
// catch (IOException e)
// // TODO Auto-generated catch block
// e.printStackTrace();
//


/***** 如果你不需要排列只要组合，删除这段就可以了然后打印sb.toString()****/

count++;
flag = false;


order[k]++; // 在当前位置选择新的数字
if (order[k] == n) // 当前位置已无数字可选，回溯

order[k--] = 0;
continue;


if (k < m) // 更新当前位置的下一位置的数字

order[++k] = order[k - 1];
continue;


if (k == m)
flag = true;


order = null;
return count;


public static void main(String[] args) throws Exception
char[] car= 'A','B','C','D','E';
FileOutputStream out = new FileOutputStream(new File("C:/add0.txt"));

Bd9Test bt = new Bd9Test();
bt.buffout =new BufferedOutputStream(out);
for (int i = 2; i < car.length+1; i++)
bt.combine(car, car.length, i);

bt.buffout.flush();
bt.buffout.close();



import java.math.BigInteger;

public class PermutationGenerator

private int[] a;
private BigInteger numLeft;
private BigInteger total;

public PermutationGenerator(int n)
if (n < 1)
throw new IllegalArgumentException("Min 1");

a = new int[n];
total = getFactorial(n);
reset();


public void reset()
for (int i = 0; i < a.length; i++)
a[i] = i;

numLeft = new BigInteger(total.toString());


public BigInteger getNumLeft()
return numLeft;


public BigInteger getTotal()
return total;


public boolean hasMore()
return numLeft.compareTo(BigInteger.ZERO) == 1;


private static BigInteger getFactorial(int n)
BigInteger fact = BigInteger.ONE;
for (int i = n; i > 1; i--)
fact = fact.multiply(new BigInteger(Integer.toString(i)));

return fact;


public int[] getNext()

if (numLeft.equals(total))
numLeft = numLeft.subtract(BigInteger.ONE);
return a;


int temp;

// Find largest index j with a[j] < a[j+1]

int j = a.length - 2;
while (a[j] > a[j + 1])
j--;


// Find index k such that a[k] is smallest integer
// greater than a[j] to the right of a[j]

int k = a.length - 1;
while (a[j] > a[k])
k--;


// Interchange a[j] and a[k]

temp = a[k];
a[k] = a[j];
a[j] = temp;

// Put tail end of permutation after jth position in increasing order

int r = a.length - 1;
int s = j + 1;

while (r > s)
temp = a[s];
a[s] = a[r];
a[r] = temp;
r--;
s++;


numLeft = numLeft.subtract(BigInteger.ONE);
return a;



参考技术A 先占个位置,一会找到好算法把代码帖上来

Java 全排列与组合

Permutation

• 全排列
• • 概念
  • 分析
• 代码展示
• 组合
• • 概念
  • 枚举1-n所有组合，随机选取任意多个
  • • 分析
    • 代码展示
  • 枚举1-n所有组合，随机选取m个数
  • • 代码展示

排列组合是组合学最基本的概念。
所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。
组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。
----- 百度百科

全排列

概念

一般地说，从n个不同元素中，任取m(m≤n)个元素，按照一定的顺序排成一列，这就叫做从n个元素中取出m个元素的一个排列。

公式：

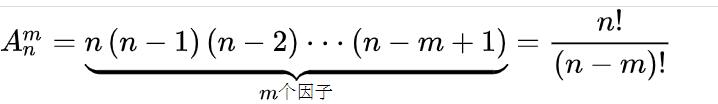
当 m=n 时，便称为全排列

此外规定0! = 1

因此：全排列公式：n！

分析

举例：
1，2，3的全排列有：

1，2，3
1，3，2
2，1，3
2，3，1
3，1，2
3，2，1

考虑建立二叉树

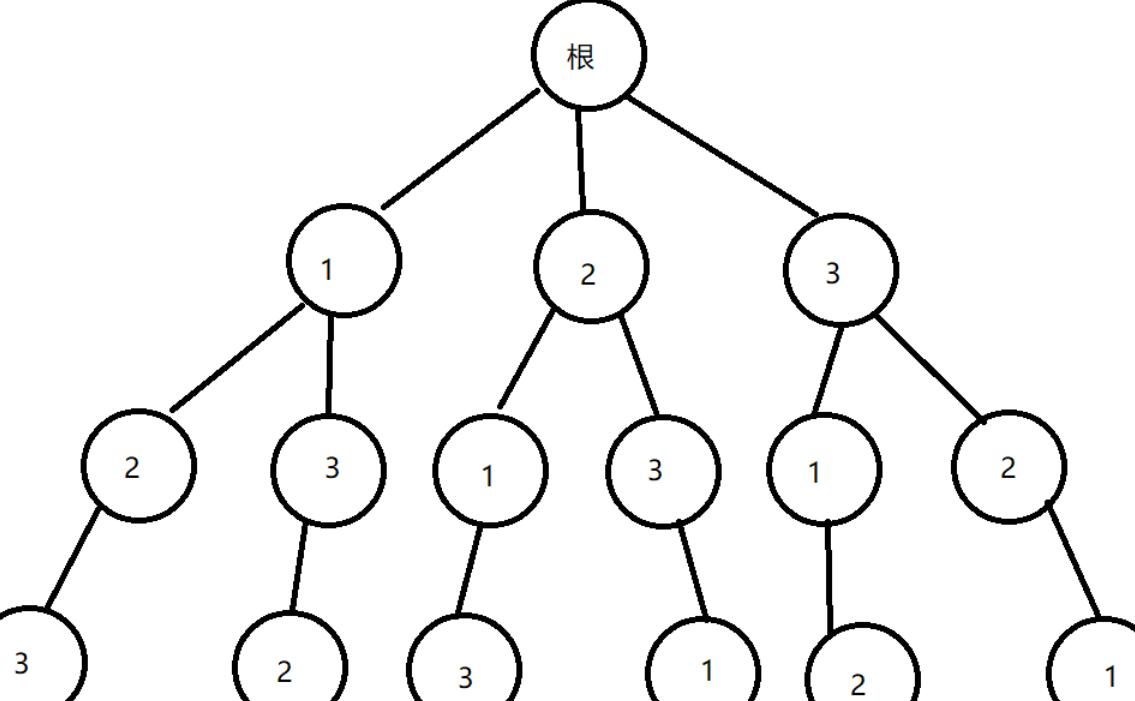
对于每一种排列的，都需要选择 首元素，之后第一个元素与剩下的元素依次类推，每一步都选择一个元素，直到全部元素选择完毕。
考虑使用递归，底层是栈，每一次出栈，后我们还原上一次的现场，重现修改之前选择的元素，再次进栈。

代码展示

import java.util.Arrays;

public class Main {
    static int[] a;
    public static void main(String[] args) {
        a = new int[]{1, 2, 3, 4};
        fullSort(0, a.length-1);
    }
    public static void fullSort(int s, int e) {
        // 递归结束条件
        if (s == e) {
            System.out.println(Arrays.toString(a));
        }
        // 脑海中形成二叉树的形状，对于当前需要选择一个元素做首，之后从该元素向下递归
        // 对于 s-e 所有元素都可放在首，因此 for循环，每次递归后，回溯需要还原现场
        for (int i = s; i <= e; i++) {
            // 交换首元素
            swap(s, i);
            fullSort(s+1, e);
            // 交换元素复原，不影响下一次的选择
            swap(s, i);
        }
    }
    // 交换元素函数
    public static void swap(int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

结果：

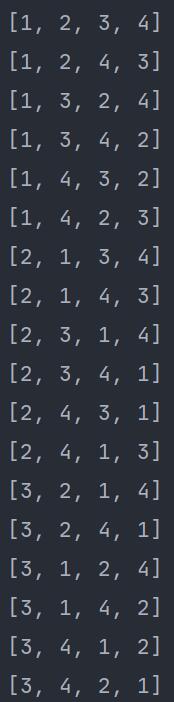
组合

概念

组合的定义：

从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；
从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。
用符号 C(n,m) 表示。

公式：

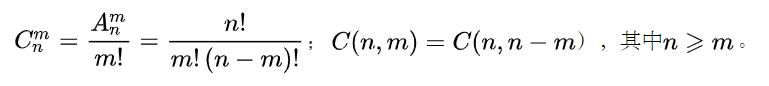
或者是：
n * (n-1)…(n-m+1) / m!

枚举1-n所有组合，随机选取任意多个

分析

例如：
n=2，有3种情况：

1
2
12

对于1-n 的每一个数，我们有选择与不选择两种情况，对于每次选择之后，求解子问题，一直到结束条件，考虑使用递归，注意每次选择后，需要还原现场。

代码展示

import java.util.Scanner;
import java.util.Vector;

// 枚举1-n所有组合，随机选取任意多个
public class _01_enumerateAll {
    static int n;
    static Vector<Integer> vector = new Vector<>();

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        calc(1);
    }

    public static void calc(int x) {
    	// 递归结束条件，遍历到最后
        if (x == n+1) {
            for (int i : vector) {
                System.out.print(i + " ");
            }
            System.out.println();
            return;
        }
        // 不选x分支
        calc(x+1);
        // 选择x
        vector.add(x);
        // 求解子问题
        calc(x+1);
        // 回溯上一个问题之前，还原现场
        vector.remove((Object)x);
    }
}

枚举1-n所有组合，随机选取m个数

与上面类似，只需修改递归结束条件即可

代码展示

import java.util.Scanner;
import java.util.Vector;

// 枚举1-n所有组合，随机选取m个数
public class _02_enumerateN {
    static int n, m;
    static Vector<Integer> vector = new Vector<>();

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();

        calc(1);

    }

    public static void calc(int x) {
    	// 剪枝操作，减去不必要的递归，提前出栈
    	// 当选择的数 > m 时，或者 剩下的数，不够选时，return;
        if (vector.size() > m || vector.size() + (n-x+1) < m)
            return;

        if (vector.size() == m) {
            for (int i : vector) {
                System.out.print(i + " ");
            }
            System.out.println();
            return;
        }
        // 不选x分支
        calc(x+1);
        // 选择x
        vector.add(x);
        // 求解子问题
        calc(x+1);
        // 回溯上一个问题之前，还原现场
        vector.remove((Object)x);
    }
}

感谢
努力
加油