GBDT算法

Posted 2023-04-13

参考技术A

        对于AdaBoost，可以将其视为一个将多个弱分类器线性组合后对数据进行预测的算法，该模型可以表示为：

        为基函数（即单个弱分类器）， 为基函数的参数（即弱分类器中特征的权重向量）， 为基函数的系数（即弱分类器在线性组合时的权重）， 就是基函数的线性组合。
        给定训练数据和损失函数 的条件下，构建最优加法模型 的问题等价于损失函数最小化：

        这个公式展现了AdaBoost算法的核心过程。

        我们可以利用前向分布算法来求解上一个式子的最优参数。前向分布算法的核心是 从前向后，每一步计算一个基函数及其系数，逐步逼近优化目标函数式 ，就可以简化优化的复杂度。

        M-1个基函数的加法模型为：

        M个基函数的加法模型：

        由上面两式得：

        由这个公式和公式(2)得极小化损失函数:

        算法思路如下：

        1. 初始化

        2. 对m=1,2,...,M:

                a. 极小化损失函数： 得到参数

                b. 更新：

        3. 得到加法模型：

        这样，前向分布算法将同时求解从m=1到M所有参数 的优化问题化简为逐次求解各个 的优化问题。

        Freidman提出了梯度提升算法，算法的核心是利用损失函数的负梯度将当前模型的值作为回归问题提升树算法中的残差的近似值，去拟合一个回归树。
        GBDT的思想就是不断去拟合残差，使残差不断减少。用一个通俗的例子来讲假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。（参考 集成学习之Boosting-gbdt ）GBDT中每次迭代构造的Cart树都是用前一轮的残差拟合的。
        第t轮第i个样本的损失函数的负梯度表示为：

        利用 我们可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域 其中J为叶子节点个数。

        针对每一个叶子节点里的样本，我们求出使损失函数最小的 输出值 :

        这样我们就得到了本轮的决策树拟合函数：

        从而本轮最终得到的强学习器的表达式如下：

        通过损失函数的负梯度来拟合，是一种通用的拟合损失误差的办法。无论是分类问题还是回归问题，我们都可以通过其损失函数的负梯度的拟合，从而用GBDT来解决我们的分类和回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。

d. 分位数损失：它对应的是分位数回归的损失函数。

输入： 训练样本
迭代次数（基学习器数量）： T
损失函数： L
输出： 强学习器H(x)

算法流程

        对于二元GBDT，其对数损失函数在之前已经给出：

        其中 此时的负梯度误差为：

        对于生成的决策树，各个叶子节点的最佳负梯度拟合值为：

        由于这个式子不易优化，一般使用近似值代替：

        除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二分类GBDT与GBDT回归算法过程相同。

        多分类GBDT的损失函数在之前也已经给出过：

        样本属于第k类的概率 的表达式为：

        结合上面两个式子可以求出第t轮第i个样本对应类别 l 的负梯度误差为：

        可以看出，其实这里的误差就是样本i对应类别l的真实概率和t-1轮预测概率的差值。

        对于生成的决策树，各个叶子节点的最佳负梯度拟合值为：

        由于上式比较难优化，一般用近似值代替：

        除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，多分类GBDT与二分类GBDT以及GBDT回归算法过程相同。

        为了防止GBDT过拟合，需要对其进行正则化。主要有三种方式：

        1. 给每棵树的输出结果乘上一个步长(学习率) a 。之前的弱学习器的迭代式改为：

        2. 通过子采样比例进行正则化。GBDT每一轮建树时样本从原始训练集中采用无放回随机抽样的方式产生。若采样比例取1，则采用全部样本进行训练。为了防止过拟合，同时又要防止样本拟合偏差较大(欠拟合)，要合理取值，常用 [0.5, 0.8]

        3. 对弱学习器(CART)进行正则化剪枝：控制树的最大深度、节点最少样本数、最大叶子节点数、节点分支的最小样本数等。

优点 ：

缺点 :

        由于弱学习器之间存在依赖关系，难以并行训练数据

boosting框架相关参数 ：

弱学习器参数 ：

        GBDT的适用面非常广，几乎可以用于所有回归问题（线性/非线性），也可以用于分类问题。

MLlib--GBDT算法

转载请标明出处http://www.cnblogs.com/haozhengfei/p/8b9cb1875288d9f6cfc2f5a9b2f10eac.html 

---

GBDT算法

江湖传言：GBDT算法堪称算法界的倚天剑屠龙刀

 

GBDT算法主要由三个部分组成：

 

                   – 

Regression Decistion Tree（即

DT)

   

回归树

                   – 

Gradient Boosting（即GB)

   

迭代提升

                   – 

Shrinkage(渐变)

   

渐变

1.决策树

1.1决策树的分类

决策树	分类决策树	用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。
	回归决策树	预测实数值，如明天的温度、用户的年龄、网页的相关程度

强调：回归决策树的结果（数值）加减是有意义的，但是分类决策树是没有意义的，因为它是类别

1.2什么是回归决策树？

   回归树决策树的总体流程可以类比分类树，比如C4.5分类树在每次分枝时，是穷举每一个feature的每一

个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的feature和阈值，按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条

件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。在回归树当中，每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平

均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差--即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和 除以 N。这很好理解

，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子

节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

1.3回归决策树划分的原则_CART算法

   CART算法思想：计算子节点的均方差，均方差越小，回归决策树越好。

2.GBDT算法_Boosting迭代

   即通过迭代多棵树来共同决策

   GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差(比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵

树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学)，这个残差就是一个加预测值后能得真实值的累加量。这一过程离不开Boosting迭代。

2.2图解Boosting迭代

 

Adaboost算法是另一种boost方法，它按分类对错，分配不同的weight，计算时使用这些weight，从而让“错分的样本权重越来越大，使它们更被重视”。

 

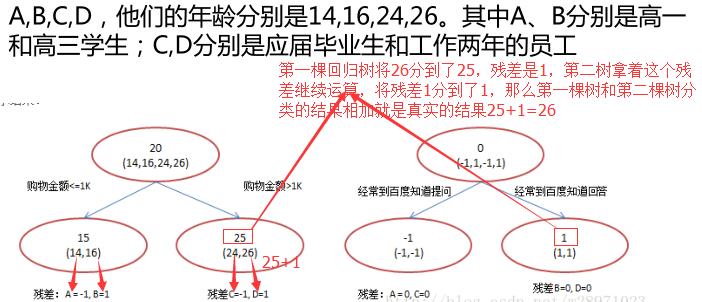
2.3GBDT算法_构建决策树的步骤

• 0. 表示给定一个初始值

• 1. 表示建立M棵决策树（迭代M次）

• 2. 表示对函数估计值F(x)进行Logistic变换

• 3. 表示对于K个分类进行下面的操作（其实这个for循环也可以理解为向量的操作，每一个样本点xi都对应了K种可能的分类yi，所以yi, F(xi), p(xi)都是一个K维的向量，这样或许容易理解一点）

• 4. 表示求得残差减少的梯度方向

• 5. 表示根据每一个样本点x，与其残差减少的梯度方向，得到一棵由J个叶子节点组成的决策树

• 6. 为当决策树建立完成后，通过这个公式，可以得到每一个叶子节点的增益（这个增益在预测的时候用的）

每个增益的组成其实也是一个K维的向量，表示如果在决策树预测的过程中，如果某一个样本点掉入了这个叶子节点，则其对应的K个分类的值是多少。比如说，GBDT得到了三棵决策树，一个样本点在预测的时候，也会掉入3个叶子节点上，其增益分别为（假设为3分类的问题）： (0.5, 0.8, 0.1), (0.2, 0.6, 0.3), (0.4, 0.3, 0.3)，那么这样最终得到的分类为第二个，因为选择分类2的决策树是最多的。

• 7. 将当前得到的决策树与之前的那些决策树合并起来，作为新的一个模型

2.4GBDT和其他的比较

2.4.1GBDT和随机森林的比较

问题：GBDT和随机森林都是基于决策树的高级算法，都可以用来做分类和回归，那么什么时候用GBDT？ 什么时候用随机森林？

    1.二者构建树的差异：

            随机森林采取有放回的抽样构建的每棵树基本是一样的，多棵树形成森林，采用投票机制决定最终的结果。

            GBDT通常只有第一个树是完整的，当预测值和真实值有一定差距时（残差），下一棵树的构建会拿到上一棵树最终的残差作为当前树的输入。GBDT每次关注的不是预测错误的样本，没有对错一说，只有离标准相差的远近。

    2.因为二者构建树的差异，随机森林采用有放回的抽样进行构建决策树，所以随机森林相对于GBDT来说对于异常数据不是很敏感，但是GBDT不断的关注残差，导致最后的结果会非常的准确，不会出现欠拟合的情况，但是异常数据会干扰最后的决策。

    综上所述：如果数据中异常值较多，那么采用随机森林，否则采用GBDT。

2.4.2GBDT和SVM

GBDT和SVM是最接近于神经网络的算法，神经网络每增加一层计算量呈几何级增加，神经网络在计算的时候倒着推，每得到一个结果，增加一些成分的权重，神经网络内部就是通过不同的层次来训练，然后增加比较重要的特征，降低那些没有用对结果影响很小的维度的权重，这些过程在运行的时候都是内部自动做。如果GBDT内部核函数是线性回归（逻辑回归），并且这些回归的离散化，归一化做得非常好，那么就可以赶得上神经网络。GBDT底层是线性组合来给我们做分类或者拟合，如果层次太深，或者迭代次数太多，就可能出现过拟合，比如原来用一条线分开的两种数据，我们使用多条线来分类。

2.4.3如何用回归决策树来进行分类？

   把回归决策树最终的叶子节点上面的数据进行一个逻辑变换（logistic），然后对这样的数据进行逻辑回归，就可以使用回归决策树来进行分类了。

2.4.4数据处理--归一化

归一化：

   不同的特征数量级不一样，（第一个特征0-1，第二个特征1000-10000，这时候就需要归一化，都归一到0-1之间）

 

归一化两种方式：

   线性归一化 (x-min)/(max-min)

   零均值归一化 （与期望和方差有关）；

2.5回归决策树code

生成测试数据LogisticRegressionDataGenerator

回归决策树代码测试GBDT_new

   bootstingStrategy.setLearningRate(0.8)`//设置梯度，迭代的快慢

 1 import org.apache.log4j.{Level, Logger}
 2 import org.apache.spark.mllib.feature.{StandardScaler, StandardScalerModel}
 3 import org.apache.spark.mllib.regression.LabeledPoint
 4 import org.apache.spark.mllib.tree.{GradientBoostedTrees, DecisionTree}
 5 import org.apache.spark.mllib.tree.configuration.{BoostingStrategy, Algo}
 6 import org.apache.spark.mllib.tree.impurity.Entropy
 7 import org.apache.spark.mllib.util.MLUtils
 8 import org.apache.spark.rdd.RDD
 9 import org.apache.spark.{SparkConf, SparkContext}
10 
11 /**
12   * Created by hzf
13   */
14 object GBDT_new {
15 //    E:\\IDEA_Projects\\mlib\\data\\GBDT\\train E:\\IDEA_Projects\\mlib\\data\\GBDT\\train\\model 10 local
16     def main(args: Array[String]) {
17         Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
18         if (args.length < 4) {
19             System.err.println("Usage: DecisionTrees <inputPath> <modelPath> <maxDepth> <master> [<AppName>]")
20             System.err.println("eg: hdfs://192.168.57.104:8020/user/000000_0 10 0.1 spark://192.168.57.104:7077 DecisionTrees")
21             System.exit(1)
22         }
23         val appName = if (args.length > 4) args(4) else "DecisionTrees"
24         val conf = new SparkConf().setAppName(appName).setMaster(args(3))
25         val sc = new SparkContext(conf)
26 
27         val traindata: RDD[LabeledPoint] = MLUtils.loadLabeledPoints(sc, args(0))
28         val features = traindata.map(_.features)
29         val scaler: StandardScalerModel = new StandardScaler(withMean = true, withStd = true).fit(features)
30         val train: RDD[LabeledPoint] = traindata.map(sample => {
31             val label = sample.label
32             val feature = scaler.transform(sample.features)
33             new LabeledPoint(label, feature)
34         })
35         val splitRdd: Array[RDD[LabeledPoint]] = traindata.randomSplit(Array(1.0, 9.0))
36         val testData: RDD[LabeledPoint] = splitRdd(0)
37         val realTrainData: RDD[LabeledPoint] = splitRdd(1)
38 
39         val boostingStrategy: BoostingStrategy = BoostingStrategy.defaultParams("Classification")
40         boostingStrategy.setNumIterations(3)
41         boostingStrategy.treeStrategy.setNumClasses(2)
42         boostingStrategy.treeStrategy.setMaxDepth(args(2).toInt)
43         boostingStrategy.setLearningRate(0.8)
44         //  boostingStrategy.treeStrategy.setCategoricalFeaturesInfo(Map[Int, Int]())
45         val model = GradientBoostedTrees.train(realTrainData, boostingStrategy)
46 
47         val labelAndPreds = testData.map(point => {
48             val prediction = model.predict(point.features)
49             (point.label, prediction)
50         })
51         val acc = labelAndPreds.filter(r => r._1 == r._2).count.toDouble / testData.count()
52 
53         println("Test Error = " + acc)
54 
55         model.save(sc, args(1))
56     }
57 }

View Code

设置运行参数

1. E:\\IDEA_Projects\\mlib\\data\\GBDT\\train E:\\IDEA_Projects\\mlib\\data\\GBDT\\train\\model 10 local