特征预处理-对数变换
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了特征预处理-对数变换相关的知识,希望对你有一定的参考价值。
参考技术A 我们在数据预处理过程中经常见到对于有偏数据进行log变换,变换后的数据能更加接近正态分布。关于有偏数据的判定,一般是计算偏度值skewness。
但是, 为什么有偏数据经过对数变换后会更加接近正态分布呢?
原因在于对数最基本的运算法则: logaA-logaB=loga(A/B)
如上图所示,我们可以看到上图的原始数据经过log变换(以e为底)后数据呈现接近出了正态分布的形态。原始数据的分布集中在左侧,有极少数的数据较大,分布在右侧;数据的中位数大约在150附近。
中位数两边的数据样本量大致相当,150取ln后结果大约为5;
对于数据样本中的极大值而言(例如750),取ln后的约等于6.6;对于数据样本中的极小值而言(例如30),取ln后的约等于3.4。他们变换后的结果距离中位数取ln的距离均为1.6(6.6-5和5-3.4),也就是ln(750)-ln(150)=ln(5)=ln(150)-ln(30)。
这就是取log之后数据能更加接近正态分布的原因。
【参考链接】https://stats.stackexchange.com/questions/107610/what-is-the-reason-the-log-transformation-is-used-with-right-skewed-distribution
数据变换
数据的变换
- 数据变换主要是对数据进行规范化处理,将数据转换成"适当的"形式,以适用于挖掘任务及算法的需求.
- 简单的函数变换:是对原始数据进行某些函数变换,常用的变换包括平方,开方,取对数,差分运算等
- 简单的函数变换常用来将不具有正太分布的数据变换成具有正太分布的数据.在时间序列分析中,有时简单的对数变换或者差分运算就可以将非平稳序列转换成平稳序列,在数据挖掘中,简单的函数变换可能更有必要,比如个人年收入的取值范围10000元到10亿元,这是一个很大的区间,使用对数变换对其进行压缩是常用的一种变换处理方法.
- 规范化
- 数据规范化(归一化)吹数据是数据挖掘的一箱基础工作,不同的评价指标往往具有不同的量纲,数据间差别可能很大,不进行处理可能会影响到数据处理的结果,为了消除指标间的量纲和取值范围差异的影响,,需要进行标准化处理,将数据按照比例进行缩放,使之落入一个特定的区域,便于进行综合分析.
- 数据规范化对于基于距离的挖掘算法尤为重要
- 最小-最大规范化
- 最小-最大化也称为离差标准化,是对原始数据的线性变化,将数值映射到[0.1]之间,其转换公式如下:
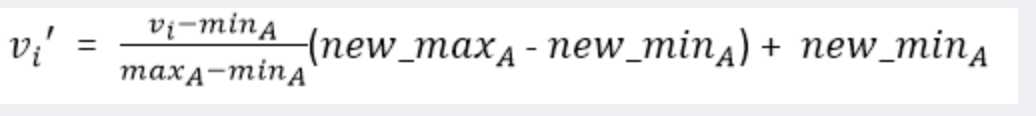
- 其中,max为样本数据的最大化,min为样本数据的最小值,max-min为极差.离差标准化保留了原来数据中存在的关系,是消除量纲和数据取值范围影响最简单方法.这种方法的缺点是若数值集中且某个数值很大,则规范化后各值会接近于0,并且将会相差不大.若将来遇到超过目前属性[min,max]取值范围,会引起系统出错,需要重新确定min和max
- 零-均值规范化
- 零-均值规范化也称标准差标准化,经过处理的数据均值为0,标准差为1,转化公式为:
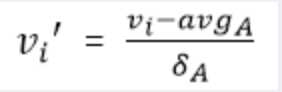
- 其中分母为原始数据的标准差,分子为每一个数据与均值的差,这一方法是当前用的最多的数据标准化方法.
- 小数定标规范化
- 通过移动属性值的小数位数,将属性值映射到[-1,1]之间,移动的小数位取决于属性值绝对值的最大值.其公式如下
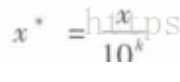
- 最小-最大规范化
- 连续属性离散化
以上是关于特征预处理-对数变换的主要内容,如果未能解决你的问题,请参考以下文章