背包问题怎样给出符号说明,目标函数和约束条件
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了背包问题怎样给出符号说明,目标函数和约束条件相关的知识,希望对你有一定的参考价值。
参考技术A ——matlab不仅具有数值运算功能,还开发了在matlab环境下实现符号计算的工具包SymbolicMathToolbox符号运算的功能符号表达式,符号矩阵的创建符号线性代数因式分解,和简化符号代数方程求解符号微积分符号微分方程一,符号运算的基本操作什么是符号运算与数值运算的区别※数值运算中必须先对变量赋值,然后才能参与运算.※符号运算无须事先对独立变量赋值,运算结果以标准的符号形式表达.特点:运算对象可以是没赋值的符号变量可以获得任意精度的解SymbolicMathToolbox——符号运算工具包通过调用Maple软件实现符号计算的.maple软件——主要功能是符号运算,它占据符号软件的主导地位.2.符号变量与符号表达式f='sin(x)+5x'f——符号变量名sin(x)+5x——符号表达式''——符号标识符号表达式一定要用''单引号括起来matlab才能识别.''的内容可以是符号表达式,也可以是符号方程.例:f1='ax^2+bx+c'——二次三项式f2='ax^2+bx+c=0'——方程f3='Dy+y^2=1'——微分方程※符号表达式或符号方程可以赋给符号变量,以后调用方便;也可以不赋给符号变量直接参与运算3.符号矩阵的创建数值矩阵A=[1,2;3,4]A=[a,b;c,d]——不识别用matlab函数sym创建矩阵(symbolic的缩写)命令格式:A=sym('[]')※符号矩阵内容同数值矩阵※需用sym指令定义※需用''标识例如:A=sym('[a,2*b;3*a,0]')A=[a,2*b][3*a,0]这就完成了一个符号矩阵的创建.注意:符号矩阵的每一行的两端都有方括号,这是与matlab数值矩阵的一个重要区别.用字符串直接创建矩阵模仿matlab数值矩阵的创建方法需保证同一列中各元素字符串有相同的长度.例:A=['[a,2*b]';'[3*a,0]']A=[a,2*b][3*a,0]符号矩阵的修改a.直接修改可用,键找到所要修改的矩阵,直接修改b.指令修改用A1=sym(A,,,'new')来修改.用A1=subs(A,'new','old')来修改A1=subs(S,'old','new')例如:A=[a,2*b][3*a,0]A1=sym(A,2,2,'4*b')A1=[a,2*b][3*a,4*b]A(2,2)='4*b'A3=[a,2*b][3*a,4*b]A2=subs(A1,'c','b')A2=[a,2*c][3*a,4*c]符号矩阵与数值矩阵的转换将数值矩阵转化为符号矩阵函数调用格式:sym(A)A=[1/3,2.5;1/0.7,2/5]A=0.33332.50001.42860.4000sym(A)ans=[1/3,5/2][10/7,2/5]将符号矩阵转化为数值矩阵函数调用格式:numeric(A)A=[1/3,5/2][10/7,2/5]numeric(A)ans=0.33332.50001.42860.4000二,符号运算符号矩阵运算数值运算中,所有矩阵运算操作指令都比较直观,简单.例如:a=b+c;a=a*b;A=2*a^2+3*a-5等.而符号运算就不同了,所有涉及符号运算的操作都有专用函数来进行符号矩阵运算的函数:symadd(a,d)——符号矩阵的加symsub(a,b)——符号矩阵的减symmul(a,b)——符号矩阵的乘symdiv(a,b)——符号矩阵的除sympow(a,b)——符号矩阵的幂运算symop(a,b)——符号矩阵的综合运算例1:f='2*x^2+3*x-5';g='x^2+x-7';h=symadd(f,g)h=3*x^2+4*x-12例2:f='cos(x)';g='sin(2*x)';symop(f,'/',g,'+',f,'*',g)ans=cos(x)/sin(2*x)+cos(x)*sin(2*x)例1:f=2*x^2+3*x-5;g=x^2+x-7;>>symsx>>f=2*x^2+3*x-5;g=x^2+x-7;>>h=f+gh=3*x^2+4*x-12例2:f=cos(x);g=sin(2*x);>>symsx>>f=cos(x);g=sin(2*x);>>f/g+f*gans=cos(x)/sin(x)+cos(x)*sin(x)符号运算函数:symsize——求符号矩阵维数charploy——特征多项式determ——符号矩阵行列式的值eigensys——特征值和特征向量inverse——逆矩阵transpose——矩阵的转置jordan——约当标准型simple——符号矩阵简化2.任意精度的数学运算在symbolic中有三种不同的算术运算:数值类型matlab的浮点算术运算有理数类型maple的精确符号运算vpa类型maple的任意精度算术运算浮点算术运算1/2+1/3--(定义输出格式formatlong)ans=0.83333333333333符号运算sym(1/2)+(1/3)ans=5/6--精确解任意精度算术运算digits(n)——设置可变精度,缺省16位vpa(x,n)——显示可变精度计算digits(25)vpa(1/2+1/3)ans=.8333333333333333333333333vpa(5/6,40)ans=.8333333333333333333333333333333333333333a=sym('[1/4,exp(1);log(3),3/7]')a=[1/4,exp(1)][log(3),3/7]vpa(a,10)ans=[.2500000000,2.718281828][1.098612289,.4285714286]3.符号微积分与积分变换diff(f)—对缺省变量求微分diff(f,v)—对指定变量v求微分diff(f,v,n)—对指定变量v求n阶微分int(f)—对f表达式的缺省变量求积分int(f,v)—对f表达式的v变量求积分int(f,v,a,b)—对f表达式的v变量在(a,b)区间求定积分int('被积表达式','积分变量','积分上限','积分下限')——定积分——缺省时为不定积分mtaylor(f,n)——泰勒级数ztrans(f)——Z变换Invztrans(f)——反Z变换Laplace(f)——拉氏变换Invlaplace(f)——反拉氏变换fourier(f)——付氏变换Invfourier(f)——反付氏变换例1.计算二重不定积分F=int(int('x*exp(-x*y)','x'),'y')F=1/y*exp(-x*y)例2.计算f='x*exp(-x*10)'的Z变换F=ztrans(f)F=z*exp(-10)/(z-exp(-10))^2>>symsxy>>F=int(int(x*exp(-x*y),x),y)F=1/y*exp(-x*y)>>symsx>>f=x*exp(-x*10);>>F=ztrans(f)>>F=ztrans(x*exp(-x*10);F=z*exp(-10)/(z-exp(-10))^2例3.计算指数函数eAt.用拉氏反变换法计算eAt的公式为:eAt=L-1[(SI-A)-1]系统矩阵A=eAt=结果:>>a=[01;-2-3];>>symss>>b=(s*eye(2)-a)b=[s,-1][2,s+3]>>B=inv(b)[(s+3)/(s^2+3*s+2),1/(s^2+3*s+2)][-2/(s^2+3*s+2),s/(s^2+3*s+2)]>>b11=ilaplace(sym(b,1,1));b(1,1)=b11;>>b12=ilaplace(sym(b,1,2));b(1,2)=b12;>>b21=ilaplace(sym(b,2,1));b(2,1)=b21;>>b22=ilaplace(sym(b,2,2));b(2,2)=b22;>>bb=[-exp(-2*t)+2*exp(-t),exp(-t)-exp(-2*t)][-2*exp(-t)+2*exp(-2*t),2*exp(-2*t)-exp(-t)]4.符号代数方程求解matlab符号运算能够解一般的线性方程,非线性方程及一般的代数方程,代数方程组.当方程组不存在符号解时,又无其他自由参数,则给出数值解.命令格式:solve(f)——求一个方程的解Solve(f1,f2,…fn)——求n个方程的解例1.f=ax2+bx+c求解f='a*x^2+b*x+c';solve(f)——对缺省变量x求解ans=[1/2/a*(-b+(b^2-4*a*c)^(1/2))][1/2/a*(-b-(b^2-4*a*c)^(1/2))]计算机格式一般格式例2.符号方程cos(x)=sin(x)tan(2*x)=sin(x)求解f1=solve('cos(x)=sin(x)'),f1=1/4*pisolve(f,'b')——对指定变量b求解ans=-(a*x^2+c)/xf3=matlab4.2的解[0][pi][atan(1/2*(-2*3^(1/2))^(1/2),1/2+1/2*3^(1/2))][atan(-1/2*(-2*3^(1/2))^(1/2),1/2+1/2*3^(1/2))][atan(1/2*2^(1/2)*3^(1/4)/(1/2-1/2*3^(1/2)))+pi][-atan(1/2*2^(1/2)*3^(1/4)/(1/2-1/2*3^(1/2)))-pi]f2=solve('tan(2*x)=sin(x)')f2=matlab4.2的解[0][acos(1/2+1/2*3^(1/2))][acos(1/2-1/2*3^(1/2))]numeric(f3)ans=03.14160+0.8314i0-0.8314i1.9455-1.9455numeric(f2)ans=00+0.8314i1.9455matlab4.2与6.1的对比例3.解方程组x+y+z=1x-y+z=22x-y-z=1g1='x+y+z=1',g2='x-y+z=2',g3='2*x-y-z=1'f=solve(g1,g2,g3)f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')f=z=5/6,y=-1/2,x=2/3f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')f=x:[1x1sym]f.xans=2/3y:[1x1sym]f.yans=-1/2z:[1x1sym]f.zans=5/6[x,y,z]=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')x=2/3y=-1/2z=5/65.符号微分方程求解——用一个函数可以方便地得到微分方程的符号解符号微分方程求解指令:dsolve命令格式:dsolve(f,g)f——微分方程,可多至12个微分方程的求解;g为初始条件默认自变量为'x',可任意指定自变量't','u'等微分方程的各阶导数项以大写字母D表示或或或y的一阶导数——Dyy的二阶导数——D2yy的n阶导数——Dny[y1,y2…]=dsolve(x1,x2,…xn)——返回微分方程的解一阶微分方程dsolve('Dx=y','Dy=x','x(0)=0','y(0)=1')ans=x(t)=sin(t),y(t)=cos(t)二阶微分方程dsolve('D2y=-a^2*y','y(0)=1','Dy(pi/a)=0')ans=cos(a*x)例3.y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0')ans=exp(-x)*cos(x)+exp(-x)*sin(x)ezplot(y)——方程解y(t)的时间曲线图求该方程的解三,maple函数——符号运算的扩展maple——是专门进行数学运算的软件工具,具有超强的符号运算能力,提供了几乎包括所有数学领域的专用函数matlab——依赖于maple的内核与函数库,扩展了自己的符号运算功能.matlab还设计了对maple库函数的调用功能使得已有的maple数学功能,可以扩充matlab中,作为自身符号运算能力的扩展.1.maple内核访问函数可以访问maple内核的matlab函数:maple———访问maple内核函数mapleinit——maple函数初始化mpa————maple函数定义mhelp———maple函数帮助命令procread——maple函数程序安装.maple的调用格式maple('表达式')——将表达式送至maple内核,返回符号表达式结果.maple('函数',变量1,变量2)——调用maple函数,传递给定变量.例1.5阶bernoulli多项式,计算x=3时bernoulli数.a=maple('bernoulli(5,x)')a=-1/6*x+5/3*x^3+x^5-5/2*x^4a=maple('bernoulli(5,3)')a=85例2.化简三角函数式sin2x+cos2xa=maple('simplify(sin(x)^2+cos(x)^2);')a=1例4.求f(t)=e-3tsint的拉式变换f=maple('laplace(exp(-3*t)*sin(t),t,s);')f=1/((s+3)^2+1)例4.寻找二次多项式的完全平方f(x)=x2+2x+2a=maple('completesquare(x^2+2*x+2)')a=completesquare(x^2+2*x+2)将工具包装入内存maple('with(student);')a=maple('completesquare(x^2+2*x+2)')a=(x+1)^2+1maple软件中的所有函数,在初始化时并没有完全装入内存,可用readlib指令把库函数读入内存,或用with指令将应用工具包装入内存.调用格式maple('readlib(函数名);')maple('with(工具包名);')例5.求sin(x2+y2)在x=0,y=0处泰勒级数式,8阶截断.maple('mtaylor(sin(x^2+y^2),[x=0,y=0],8)')ans=mtaylor(sin(x^2+y^2),[x=0,y=0],8)maple('readlib(mtaylor);')maple('mtaylor(sin(x^2+y^2),[x=0,y=0],8)')ans=x^2+y^2-1/6*x^6-1/2*y^2*x^4-1/2*y^4*x^2-1/6*y^62.mpa——maple变量定义任何一个matlab定义的函数f,可使用mpa语句直接调用,还可把f定义成maple变量v.maple的工作空间与matlab工作空间是相互独立的,所以f与v是属于不同工作空间中的变量mpa的调用格式:mpa('v',f)mpavff为matlab工作空间中已存在的变量例.电磁力计算公式为试I=0.5,x=0.1邻域泰勒级数,3阶截断,令常数,1.直接调用maple('readlib(mtaylor);')maple('mtaylor(k*I^2/x^2,[I=0.5,x=0.1],3);')2.定义符号函数f(matlab6.1无map函数)f='k*I^2/x^2';maple('mtaylor(f,[I=0.5,x=0.1],3);')ans=mtaylor(f,[I=.5,x=.1],3)mpa('u',f)maple('mtaylor(u,[I=0.5,x=0.1],3);')ans=25.*k-.50e3*k*(x-.1)+.10e3*k*(I-.5)+7500.000000000000*k*(x-.1)^2+.1e3*k*(I-.5)^2-.20e4*k*(I-.5)*(x-.1)注意:matlab符号运算时,可以识别matlab定义的符号变量,但在调用maple函数时,需将matlab变量定义为maple变量后,所调用的函数方可识别和执行3.mhelp——maple函数帮助命令mhelp是协助检索maple库函数的专用命令调用格式:mhelp相关词条例如:mhelpintro—maple介绍mhelpmaple—maple命令格式mhelptutorial—maple入门mhelpindex—maple检索工具词条函数词条mhelpindex用于工具包检索library——maple标准库函数packages——应用工具包libmisc——其它库函数statements——maple语句描述expressions——maple表达式datatypes——maple数据格式tables——maple表格和阵列procedures——maple程序misc——maple其它应用一般帮助文本主要包括以下部分FUNCTION——函数功能说明CALLINGSEQUENCE——调用格式PARAMETERS——调用参数说明SYNOPSIS——语法说明EXAMPLES——应用举例SEEALSO——相关词条4.maple库函数maple库函数共分四类maple内部函数:驻留函数任何条件下都可调用mhelpindex[internal]maple的外部函数—读库定义部分:调用时先执行读库命令,因此与内部函数一样可直接调用mhelpindex[external]maple的外部函数—读库装入部分maple其余外部函数需要在使用前执行maple('readlib(函数名);')命令将其装入内存mhelpindex[libmisc]maple的惰性函数—不能直接调用,还需一些函数如mod,evala,evalf等才能调用mhelpindex[intert]小结本节介绍了matlab语言的符号运算功能,通过学习应该掌握:掌握如何创建,修改符号矩阵掌握符号运算功能maple函数调用mhelp检索由线性代数我们知道A非奇异时,A的行列式不为0,此时方程的解是唯一的。数值优化基础
“数值”优化:设置算法时,要考虑舍入误差。
数值优化问题分类:
- 无约束优化 VS 约束优化
- 线性规划。目标函数和约束函数都是线性的
- 二次规划。目标函数为二次的,约束函数为线性。
- 凸优化。目标函数为凸的,约束函数为线性的。
局部解 VS 全局解
连续 VS 离散
确定 VS 随机
无约束优化问题基础
解的一阶必要条件: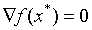
解的二阶必要条件: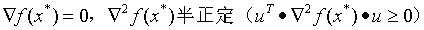
解的二阶充分条件: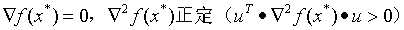
迭代算法(如何构造下一个迭代点)、终止条件
一阶、二阶、直接算法
直接算法无需使用导数,一阶算法需要使用一阶导数,二阶算法需要用到二阶导数。
算法的收敛性:
全局收敛: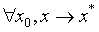
局部收敛: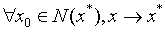
以上是关于背包问题怎样给出符号说明,目标函数和约束条件的主要内容,如果未能解决你的问题,请参考以下文章