联邦学习安全防御之同态加密

Posted 2023-04-06 武天旭

本博客地址：https://security.blog.csdn.net/article/details/124110931

 一、Paillier半同态加密算法

同态加密又可以分为全同态加密、些许同态加密和半同态加密三种形式。这其中，由于受到性能等因素的约束，当前在工业界主要使用半同态加密算法。Paillier即属于半同态加密算法，其并不满足乘法同态运算，虽然Paillier算法不是全同态加密的，但是与全同态加密算法（FHE）相比，其计算效率大大提升，因此在工业界被广泛应用。

我们以 x 表示明文，以 [[x]] 表示其对应的密文，那么Paillier 半同态加密算法满足：[[u+v]] = [[u]] +[[v]]

对于Paillier算法的加密损失函数，损失值 L 关于参数 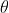 的梯度值为：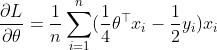

上式对应的加密梯度为：，该式仅涉及加法和数乘运算，因此Paillier算法适用于经过多项式近似之后的损失函数求解。

二、同态加密防御的具体实现

2.1、定义模型

先自定义一个模型类 LR_Model，以方便我们进行加解密。已对代码做出了具体的注释说明，具体细节阅读代码即可。

models.py

import torch 
from torchvision import models
import numpy as np

def encrypt_vector(public_key, x):
	return [public_key.encrypt(i) for i in x]
	
def encrypt_matrix(public_key, x):
	ret = []
	for r in x:
		ret.append(encrypt_vector(public_key, r))
	return ret 
		
def decrypt_vector(private_key, x):
	return [private_key.decrypt(i) for i in x]

def decrypt_matrix(private_key, x):
	ret = []
	for r in x:
		ret.append(decrypt_vector(private_key, r))
	return ret 
		
class LR_Model(object):
	def __init__ (self, public_key, w_size=None, w=None, encrypted=False):
		# w_size: 权重参数数量
		# w: 是否直接传递已有权重，w和w_size只需要传递一个即可
		# encrypted: 是明文还是加密的形式
		self.public_key = public_key
		if w is not None:
			self.weights = w
		else:
			limit = -1.0/w_size 
			self.weights = np.random.uniform(-0.5, 0.5, (w_size,))
		
		if encrypted==False:
			self.encrypt_weights = encrypt_vector(public_key, self.weights)
		else:
			self.encrypt_weights = self.weights	
			
    # 用于更新加密的权重向量
	def set_encrypt_weights(self, w):
		for id, e in enumerate(w):
			self.encrypt_weights[id] = e 
		
    # 用于更新明文权重向量
	def set_raw_weights(self, w):
		for id, e in enumerate(w):
			self.weights[id] = e 
			

2.2、（客户端）本地模型训练

在本地的模型训练中，模型参数是在加密的状态下进行，其过程如下所示。已对代码做出了具体的注释说明，具体细节阅读代码即可。

client.py

import models, torch, copy
import numpy as np
from server import Server

class Client(object):
	def __init__(self, conf, public_key, weights, data_x, data_y):
		self.conf = conf
		self.public_key = public_key
		self.local_model = models.LR_Model(public_key=self.public_key, w=weights, encrypted=True)
		self.data_x = data_x
		self.data_y = data_y
		
	def local_train(self, weights):
        # 复制服务端下发的全局模型权重
		original_w = weights
        # 将本地模型的权重更新为全局模型权重
		self.local_model.set_encrypt_weights(weights)
		neg_one = self.public_key.encrypt(-1)
		
		for e in range(self.conf["local_epochs"]):
			print("start epoch ", e)
			# 每一轮都随机挑选batch_size大小的训练数据进行训练
			idx = np.arange(self.data_x.shape[0])
			batch_idx = np.random.choice(idx, self.conf['batch_size'], replace=False)
			x = self.data_x[batch_idx]
			x = np.concatenate((x, np.ones((x.shape[0], 1))), axis=1)
			y = self.data_y[batch_idx].reshape((-1, 1))
            # 在加密状态下求取加密梯度
			batch_encrypted_grad = x.transpose() * (0.25 * x.dot(self.local_model.encrypt_weights) + 0.5 * y.transpose() * neg_one)
			encrypted_grad = batch_encrypted_grad.sum(axis=1) / y.shape[0]
			
			for j in range(len(self.local_model.encrypt_weights)):
				self.local_model.encrypt_weights[j] -= self.conf["lr"] * encrypted_grad[j]

		weight_accumulators = []
		for j in range(len(self.local_model.encrypt_weights)):
			weight_accumulators.append(self.local_model.encrypt_weights[j] - original_w[j])
		
		return weight_accumulators

2.3、（服务端）生成公钥和私钥

已对代码做出了具体的注释说明，具体细节阅读代码即可。

server.py

import models, torch
import paillier
import numpy as np

class Server(object):
    # 利用paillier算法生成公钥和私钥，公钥用于加密，私钥用于解密
	public_key, private_key = paillier.generate_paillier_keypair(n_length=1024)
	def __init__(self, conf, eval_dataset):
		self.conf = conf 
		self.global_model = models.LR_Model(public_key=Server.public_key, w_size=self.conf["feature_num"]+1)
		self.eval_x = eval_dataset[0]
		self.eval_y = eval_dataset[1]
		
	def model_aggregate(self, weight_accumulator):
		for id, data in enumerate(self.global_model.encrypt_weights):
			update_per_layer = weight_accumulator[id] * self.conf["lambda"]
			self.global_model.encrypt_weights[id] = self.global_model.encrypt_weights[id] + update_per_layer
	
	def model_eval(self):
		total_loss = 0.0
		correct = 0
		dataset_size = 0
		batch_num = int(self.eval_x.shape[0]/self.conf["batch_size"])
		self.global_model.weights = models.decrypt_vector(Server.private_key, self.global_model.encrypt_weights)
		print(self.global_model.weights)
	
		for batch_id in range(batch_num):
			x = self.eval_x[batch_id*self.conf["batch_size"] : (batch_id+1)*self.conf["batch_size"]]
			x = np.concatenate((x, np.ones((x.shape[0], 1))), axis=1)
			y = self.eval_y[batch_id*self.conf["batch_size"] : (batch_id+1)*self.conf["batch_size"]].reshape((-1, 1))

			dataset_size += x.shape[0]
			wxs = x.dot(self.global_model.weights)
			pred_y = [1.0 / (1 + np.exp(-wx)) for wx in wxs]	
			pred_y = np.array([1 if pred > 0.5 else -1 for pred in pred_y]).reshape((-1, 1))
			correct += np.sum(y == pred_y)

		acc = 100.0 * (float(correct) / float(dataset_size))
		return acc
        
	# 对数据进行重新加密
    # 先利用paillier生成私钥解密，再利用公钥重新加密
	@staticmethod
	def re_encrypt(w):
		return models.encrypt_vector(Server.public_key, models.decrypt_vector(Server.private_key, w))

经典同态加密算法Paillier解读 - 原理实现和应用

摘要

随着云计算和人工智能的兴起，如何安全有效地利用数据，对持有大量数字资产的企业来说至关重要。同态加密，是解决云计算和分布式机器学习中数据安全问题的关键技术，也是隐私计算中，横跨多方安全计算，联邦学习和可信执行环境多个技术分支的热门研究方向。

本文对经典同态加密算法Pailier算法及其相关技术进行介绍，重点分析了Paillier的实现原理和性能优化方案，同时对基于公钥的加密算法中的热门算法进行了横向对比。最后介绍了Paillier算法的一些实际应用。

【关键词】：同态加密，多方安全计算，联邦学习，隐私计算

1 背景知识

1.1 同态加密

同态加密（Homomorphic Encryption，HE）[1] 是将数据加密后，对加密数据进行运算处理，之后对数据进行解密，解密结果等同于数据未进行加密，并进行同样的运算处理。同态加密的概念最初在1978年，由Ron Rivest，Leonard Adleman和Michael L. Dertouzos共同提出，旨在解决在不接触数据的前提下，对数据进行加工处理的问题。

目前，同态加密支持的运算主要为加法运算和乘法运算。按照其支持的运算程度，同态机密分为半同态加密（Partially Homomorphic Encryption, PHE）和全同态加密（Fully Homomorphic Encryption, FHE）。半同态加密在数据加密后只持加法运算或乘法运算中的一种，根据其支持的运算的不同，又称为加法同态加密或乘法同态加密。半同态加密由于机制相对简单，相对于全同态加密技术，拥有着更好的性能。全同态加密对加密后的数据支持任意次数的加法和乘法运算。

1.2 复合剩余类问题

如果存在一个数$y\in {\mathbb{Z}}_{n^2}^{\ast }$, 那么符合公式$z\equiv y^n(mod{n}^2)$的数z，称为y的模$n^2$的n阶剩余。复合剩余类问题（decisional composite residuosity assumption , DCRA)，指的是给定一个合数n和整数z，很难确定模$n^2$的n阶剩余数z是否存在。

1.3 中国剩余定理

中国剩余定理（Chinese Remainder Theorem, CRT），又称为孙子定理，源于《孙子算经》，是数论中的一个关于一元线性同余方程组的定理，说明了一元线性同余方程组有解的准则以及求解方法。

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？
翻译为数学语言为：

$$\{\begin{array}{r}x\equiv 2(mod3)\\ x\equiv 3(mod5)\\ x\equiv 2(mod7)\end{array}$$

其通用方程为：
$$\{\begin{array}{r}x\equiv a_0(mod{n}_0)\\ x\equiv a_1(mod{n}_1)\\ ...\\ x\equiv a_k(mod{n}_k)\end{array}$$

中国剩余定理的解法流程为：

1. 计算所有模数的乘积 $n={\prod }_{i=0}^k{n}_i$
2. 计算$m_i=n/n_i,c_i=m_i\ast m_i^{-1}$
3. 方程组的解为：$x={\sum }_{i=0}^k{a}_i{c}_i(modn)$

2 Paillier算法原理

2.1 Paillier简介

在Paillier算法出现之前，基于公钥加密的算法主要有两个分支：

• 以RSA为代表的，基于大数因数分解难题的公钥加密算法
• 以ElGama为代表的，基于大数离散对数难题的公钥加密算法

Paillier加密算法，由Pascal Paillier于1999年发表，给出了公钥加密算法的一个新的分支领域。Paillier基于复合剩余类难题，满足加法同态和数乘同态，具有非常高效的运行时性能。

2.2 一个典型的应用场景

图1 传统联邦学习

同态加密算法使得密文数据，在没有额外数据泄露的情况下，可以在第三方平台进行进一步加工处理。随着大规模云计算的兴起，尤其是涉及到敏感数据的云计算，同态加密算法将是其中至关重要的技术基础。我们以一个典型的联邦学习的例子为切入点，看看Paillier算法的原理和在实践中应用的问题。

假设Alice和Bob想共同训练一个网络模型，Alice和Bob各自持有一部分训练数据，并且他们不想把自己的数据泄露给对方。那么在训练期间，Alice和Bob需要交互各自训练的梯度数据，并根据双方的梯度数据，共同计算一个对双方都合适的梯度值，用来执行联合梯度下降过程。

2019年，Ligeng Zhu等人发表的“Deep Leakage from Gradients”论文中给出了一种算法[2]，可以从几次迭代的梯度数据中，推断出训练的数据，标签，模型等一系列隐私信息。这使得在分布式机器学习中，通过传输梯度数据来进联合模型训练变得不再安全。那么如果在梯度数据传输的过程中，传输的是加密后的梯度数据，并且这些加密数据可以进行二次计算，那么便可以规避梯度数据传输过程带来的安全风险。

2.3 Paillier算法

2.3.1 密钥生成

类似于RSA算法，Paillier也拥有公钥和私钥对。

• Alice选择两个大素数p=11，q=19(目前已知512bit的非对称密钥已经可以破解，实际应用中通常选用非常大的素数)
• Alice计算p和q的乘积n = p * q = 209, 并计算λ = lcm(p – 1, q - 1)
• Alice选择一个随机整数g, $g\in {\mathbb{Z}}_{n^2}^{\ast }$
• Alice定义函数$L(x)=\frac{x-1}{n}$ , 并计算模反元素 $\mu ={L(g^{\lambda }mod{n}^2)}^{-1}modn$

在上述过程中，Alice总计生成了6个数字：

p = 11
q = 19
n = 209
λ = 90
g = 147
μ = 153

Alice将 n 和g 封装成公钥 public-key = (n, g)
将λ和μ封装成私钥: private-key = (λ, μ)

2.3.2 加密

假设Bob需要加密明文m， 0 <= m < n. 且Bob收到了Alice发送过来的公钥（n, g）

• Bob选择一个随机数r,满足0 < r < n
• Bob计算加密后的密文 c = g^m.rⁿ mod n²

m = 8
r = 3
n_square = pow(n, 2) # n_square = 43681
c = gmpy2.mod(pow(g, m)*pow(r, n), n_square) # c =  32948

2.3.3 解密

假设c是Bob发送过来的密文，且$c\in {\mathbb{Z}}_{n^2}^{\ast }$
Alice计算明文$m=L(c^{\lambda }mod{n}^2)\ast \mu modn$

c = 32948
m  = gmpy2.mod(L(gmpy2.mod(pow(c, lam), n_square), n) * mu, n) # m = 8

正确性证明

为了证明解密操作的正确性，我们把加密的公式代入：
$DEC(c)=L(c^{\lambda }mod{n}^2)\ast \mu modn=L({{(g}^m{r}^{n}mod{n}^2)}^{\lambda }mod{n}^2)\ast \mu modn=L{(g}^{\lambda m}{r}^{以上是关于联邦学习安全防御之同态加密的主要内容，如果未能解决你的问题，请参考以下文章}$

阅读笔记联邦学习实战——联邦学习攻防实战

联邦学习FATE框架安装搭建 - CentOS8

经典同态加密算法Paillier解读 - 原理实现和应用

笔记︱联邦学习与隐私计算的案例集锦

笔记︱联邦学习与隐私计算的案例集锦

笔记︱联邦学习与隐私计算的案例集锦