自动控制 PID

Posted 2023-04-04

谁能给我讲讲PID控制在自动控制中的应用
万分感谢

在现在的在工业自动化控制系统中，最为常见的是由PID控制变频器，来控制电动机频率的改变从而实现速度控制。但企业在生产中，往往需要有精密稳定的压力、温度、流量、液位或转速，以此作为保证产品质量、提高生产效率、满足工艺要求的前提，这就要用到变频器的 PID 控制功能，从而实现对被控量的时时控制，以此来实现更为准确自动控制。以下简单介绍PID控制应用方法。
一、PID的工作原理
由于来自外界的各种扰动不断产生，要想达到现场控制参数值保持稳定，控制作用就必须不断地进行。若扰动出现使得现场控制参数值发生变化，现场检测元件就会将这种变化记录并传送给PID控制器，改变过程变量值（以下简称PV值），经变送器送至PID控制器的输入端，并与其给定值（以下简称SP值）进行比较得到偏差值（以下简称e值），调节器按此偏差并以我们预先设定的整定参数控制规律（将在第三节PID算法中详细推导与分析）发出控制信号，去改变调节器的开度，使调节器的开度增加或减少，从而使现场控制参数值发生改变，并趋向于给定值（SP值），以达到控制目的。
二、PID被控参数的选定
选择被控参数是控制方案设计中的重要一环，对于稳定生产、提高产品的产量、质量等都具有决定性的意义。若被控参数选择不当，则无论组成什么样的控制系统，选用多么先进的过程检测控制设备，均不会达到预期的控制效果。
因为影响控制参数值变化的扰动很多，并非所有扰动都必须加以控制，所以正确选定被控参数，显得尤为重要。选择被控参数要根据生产工艺要求，深入分析生产工艺过程，找出对产品的产量、质量、安全生产等具有决定性作用，能较好反映工艺生产状态变化的参数，而这些参数又是人工控制难以满足要求。
在实际应用中，PID参数的选择并不是唯一的，更不是随意的，要通过对过程特性进行深入分析，才能做出的正确选择。
下面是选取被控参数的一般原则：
1、选择对产品的产量、质量、安全生产等具有决定性作用的、可直接测量的工艺参数作为被控参数。
2、当不能用直接参数作为被控参数时，应该选择一个与直接参数有线性单值函数对应关系的间接参数作为被控参数。
3、被控参数必须具有足够高的灵敏度。
4、被控参数的选取，必须考虑工艺过程的合理性和所用仪表的性能。 参考技术A P是比例，当前温度与设定温度相差越大则加热功率也线性加大。
I是积分，有些系统温度与加热功率有滞后现象，只进行P控制会出现震荡，加入积分控制，在达到设定温度前提前减小加热功率。这种控制同样可以对付温度缓慢漂移的情况，通过积分使漂移变的更明显。
D是微分，可以根据变化趋势和变化速度控制加热功率，如在相同时间内温度下降幅度相差一半，则加热功率也相差一半。
通过PID参数综合控制加热功率，可以使温度很快稳定在设定值上。

参考资料：http://zhidao.baidu.com/question/15820183.html

本回答被提问者采纳

精品课设经典PID与模糊PID控制的对比与分析

【精品课设】经典PID与模糊PID控制的对比与分析（一）

目录

• 【精品课设】经典PID与模糊PID控制的对比与分析（一）
• • 0研究背景
  • 1经典PID控制的设计
  • • 1.1 经典PID控制律的设计
    • 1.2 被控对象传递函数的代码实现
    • 1.3 基于频域PID参数的Z-N整定
  • 2模糊PID控制的设计
  • • 2.1 模糊PID控制律的设计
    • 2.2 模糊PID控制的仿真结果
  • 3仿真对比与分析

---

0研究背景

写在前面：
 1.本代码基于MATLAB2019a版本，低版本或者不同版本可能会报错，mdl文件或slx文件打开可能会失败；
 2.如果运行时间过长，请观察设置参数是否一致。
 3.本博客附上算法运行图并详细介绍，如果转载请注明出处；
 4.如果本博客恰巧与您的研究有所关联，欢迎您的咨询qq1366196286 ，同时代码下载见评论的下载链接。

文档下载：https://download.csdn.net/download/qq_42249050/19746440

代码下载：https://download.csdn.net/download/qq_42249050/19746530

---

1经典PID控制的设计

1.1 经典PID控制律的设计

  PID控制律的微分方程、各个环节的影响作用、以及Simulink组成在其他博客均有论述。如读者还存在疑惑，可转到之前的博客进行观看。

基于遗传算法的PID参数整定研究（一）
参数智能整定#基于智能算法的PID参数整定研究

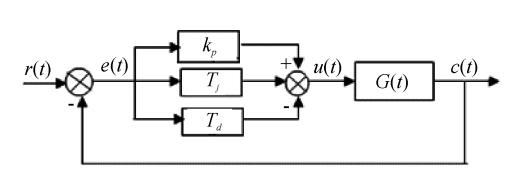
图1 PID控制结构方框图

1.2 被控对象传递函数的代码实现

   被控对象的传递函数为：

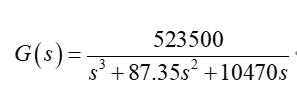
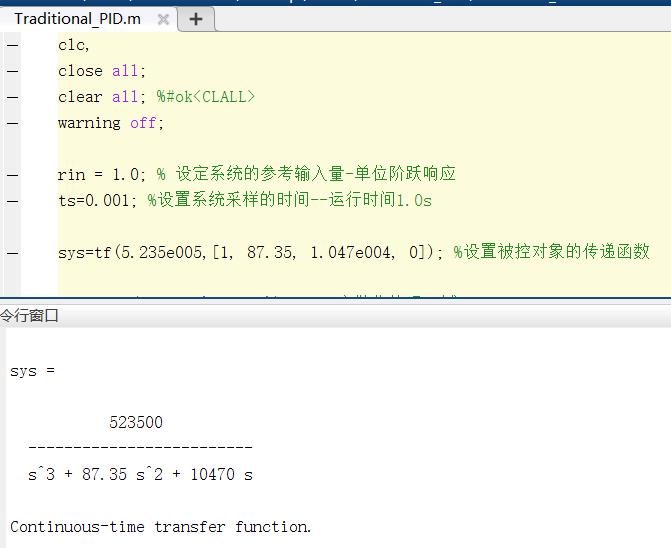
图2 被控对象运行显示图

  

---

Continuous_PID.m

clc;
clear;
% Target = 1000;  %目标值
% sys1= tf([0,300,200,350],[1,0.5,0.05,0]);   %建立被控对象传递函数 零点为-1  极点为-50
%sys2=tf([0.02 1],1);   %建立被控对象传递函数 无零点  极点为-20
%% 设置被控对象的传递函数
Target = 1.000; 
sys1=tf(5.235e005,[1, 87.35, 1.047e004, 0]); 

%% PID传递函数
% kp0=0.90; % PID控制参数的大小
% ki0=0.05;
% kd0=0.2;
Kp = 0.90;
Ki = 0.05;
Kd = 0;

sysP = Kp;
sysI = tf(Ki,[1,0]);
sysD = tf([Kd,0],1);
sysPI = parallel(sysP,sysI);  %将比例积分微分环节并联得到PID传递函数
sysPID =  parallel(sysPI,sysD);
sysG = series(sysPID,sys1);  %将两传递函数串联 得到最终的传递函数G
sysH = 1;  %反馈函数为空
sysResult = feedback(sysG,sysH);  %负反馈
step(Target * sysResult,0.5);  %串联并加入反馈后的传递函数阶跃

% %（仅绘制过渡过程的曲线，x坐标限制为[0,1]）
% p1=plot(time,Target,'-.');
% xlim([0,0.5]);
% hold on;%指令信号的曲线（即期望输入）
% p2=plot(time,y);
% xlim([0,0.5]);
% hold on;%不含积分分离的PID曲线

程序运行结果图如下：

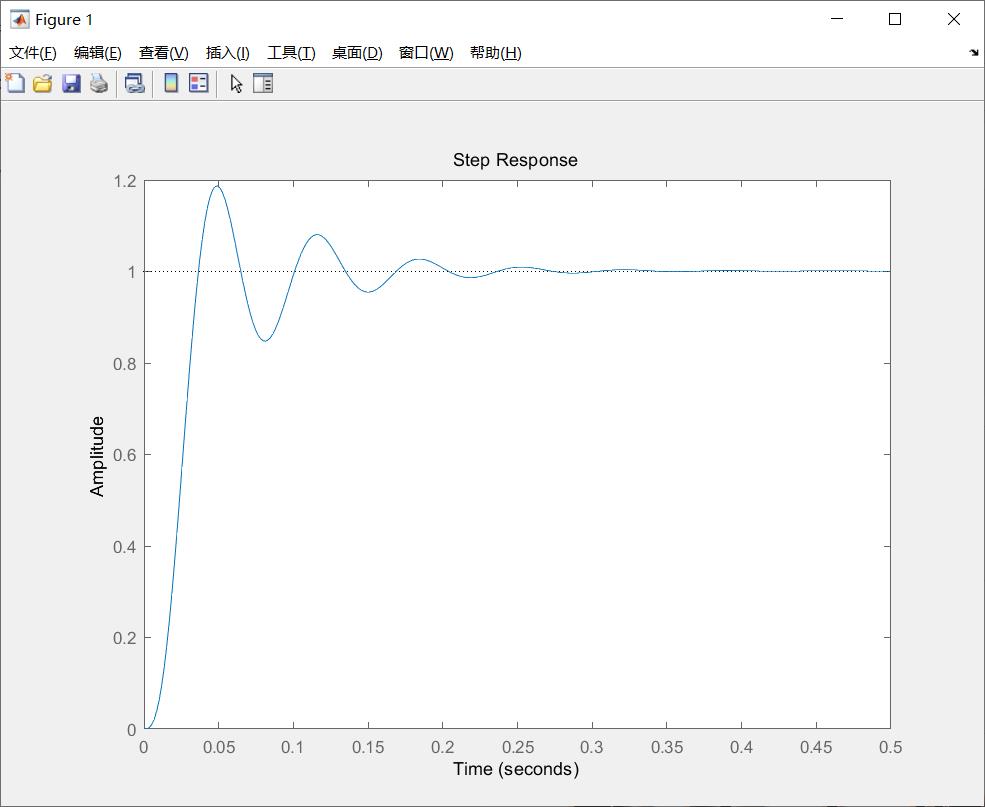
图3 连续系统下的PID仿真模拟图

Discrete_PID.m

clc;
clear;

Ts = 0.001;  %采样时间=0.001s
sys = tf([0,300,200,350],[1,0.5,0.05,0]);   %建立被控对象传递函数 无零点  极点为-10
dsys = c2d(sys,Ts,'z');      %将传递函数离散化 采样周期Ts
[num,den] = tfdata(dsys,'v');   %取出离散化后的传递函数参数

Error = 0;  %当前偏差
ErrorLast = 0; %上次偏差
ErrorSum = 0;       %累积偏差
u_1 = 0;    %上时刻控制量
u_2 = 0;    %上上时刻控制量
u_3 = 0;    %上上上时刻控制量
y_1 = 0;    %上时刻输出量
y_2 = 0;    %上上时刻输出量
y_3 = 0;    %上上上时刻输出量
y_4 = 0;    %上上上上时刻输出量
%PID参数
Kp = 1.2;    
Ki = 0.1;
Kd = 0.005;
u = zeros(1,1000);       %预先分配内存
y = zeros(1,1000);
Target = zeros(1,1000);   %目标值
time = zeros(1,1000);%时刻点（设定1000个）
for k = 1:1:1000
    time(k) = k * Ts;   %时间参数
    Target(k) = 1000;
    y(k) = num(4)*u_3 + num(3)*u_2 + num(2)*u_1 - den(4)*y_3 - den(3)*y_2 - den(2)*y_1;%系统响应输出序列      
    Error = Target(k) - y(k);   %误差信号 
    u(k) = Kp*Error + Ki*ErrorSum + Kd*(Error - ErrorLast); %系统PID控制器输出序列      
    ErrorSum = ErrorSum + Error;    %误差的累加和 
    u_3 = u_2;
    u_2 = u_1;
    u_1 = u(k);    	        %前一个的控制器输出值
    y_4 = y_3;
    y_3 = y_2;
    y_2 = y_1;
    y_1 = y(k);    	        %前一个的系统响应输出值
    ErrorLast = Error;		%前一个误差信号的值
end

%（仅绘制过渡过程的曲线，x坐标限制为[0,1]）
p1=plot(time,Target,'-.');xlim([0,0.5]);hold on;%指令信号的曲线（即期望输入）
p2=plot(time,y);xlim([0,0.5]);hold on;%不含积分分离的PID曲线

程序运行结果图如下：

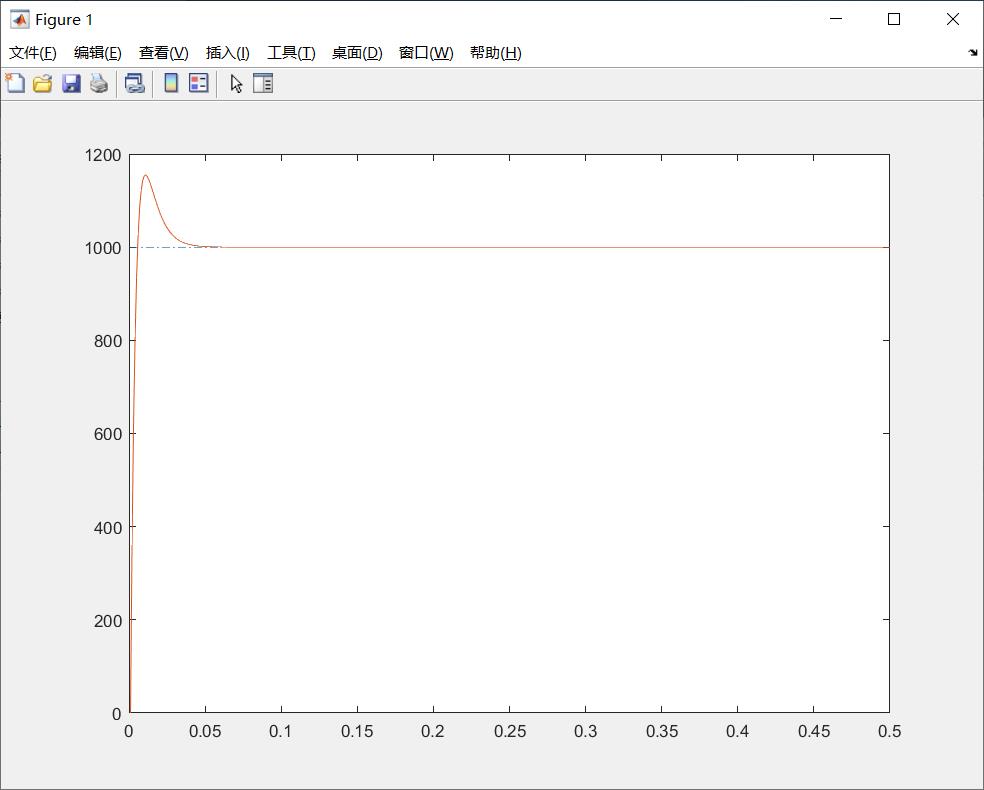
图4 离散系统下的PID仿真模拟图

1.3 基于频域PID参数的Z-N整定

  基于频域PID参数的Z-N整定可参考之前的博客文章，如下：

基于Ziegler-Nlichols 方法的PID参数整定

  运行整定程序，可得图5~图。其中图5给出了系统未补偿的根轨迹图。

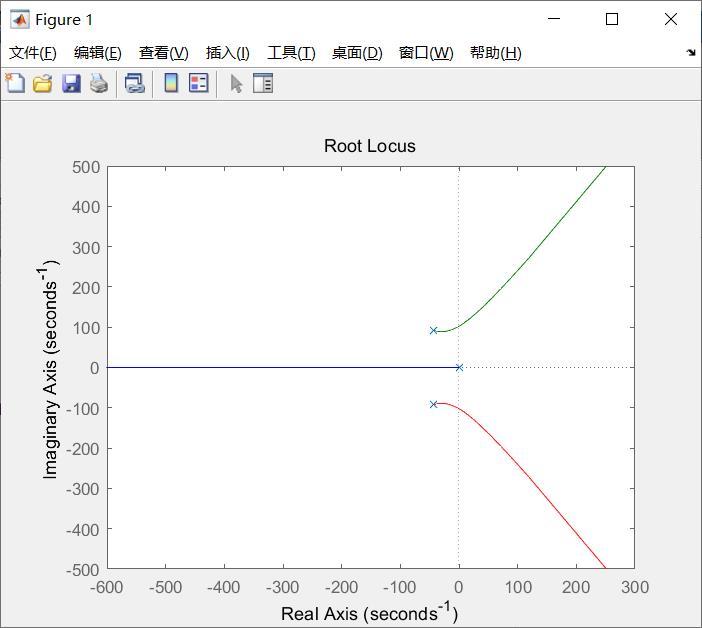
图5 系统未补偿的根轨迹图

  需要在图5上可选定穿越虚轴时的增益Km和该点的wm值，即临界状态值。其中，整定程序中，sys_pid和sysc分别为控制器和闭环系统的传递函数。

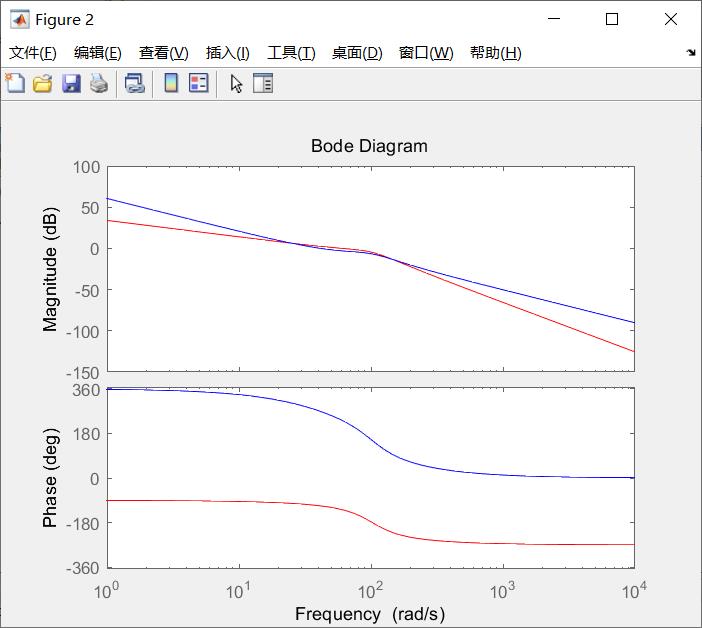
图6 整定前后的系统Bode图

  图6示出整定前后系统的伯特图，可见该系统整定后，频带拓宽，相移超前。

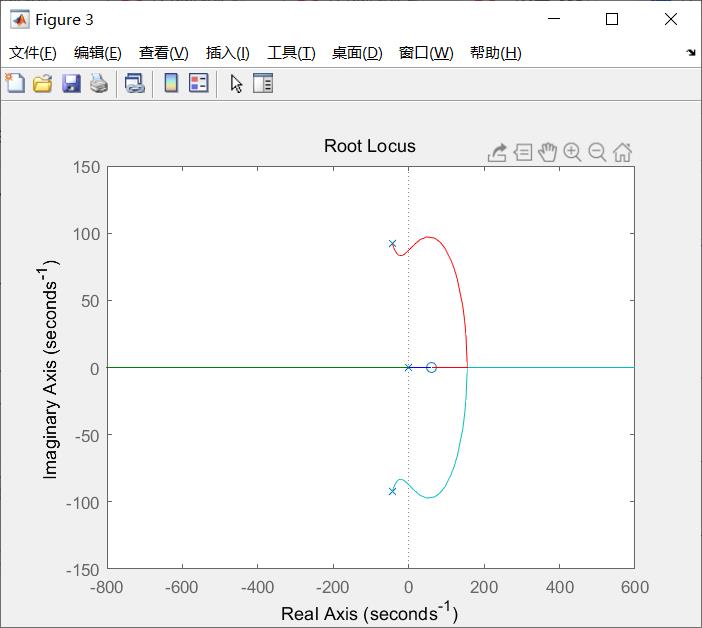
图7 系统整定后的根轨迹图

  图7示出整定后系统的根轨迹，所有极点位于负半面，达到完全稳定状态。

程序运行结果如下：

ZN_Tuning.m

%PID Controler Based on Ziegler-Nichols
clear all;
close all;

% sys=tf(400,[1,30,200,0]);
sys=tf(5.235e005,[1, 87.35, 1.047e004, 0]);


figure(1);
rlocus(sys);
[km,pole]=rlocfind(sys)

wm=imag(pole(2));
kp=0.6*km
kd=kp*pi/(4*wm)
ki=kp*wm/pi

figure(2);
grid on;
bode(sys,'r');

sys_pid=tf([kd,kp,ki],[1,0])
sysc=series(sys,sys_pid)
hold on;
bode(sysc,'b')

figure(3);
rlocus(sysc);

代码程序及仿真图

---

2模糊PID控制的设计

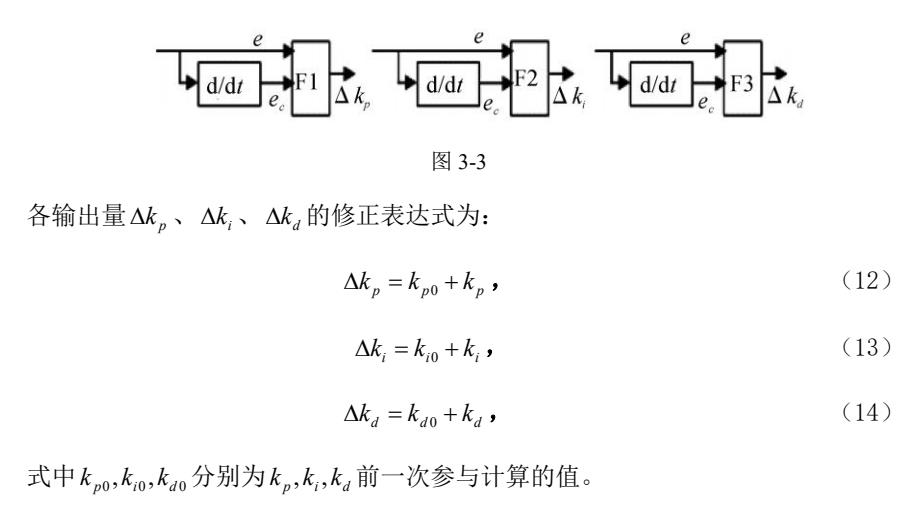
2.1 模糊PID控制律的设计

  模糊自适应PID控制器是根据对输入信号的动态跟踪，采用模糊控制以及模糊推理，对PID的各个参数进行实时调整，实现在线整定的。它是模糊控制与传统PID控制的组合体，结合了各自的控制优点，为提高控制精度提供了充分的条件。其控制原理如图8所示。

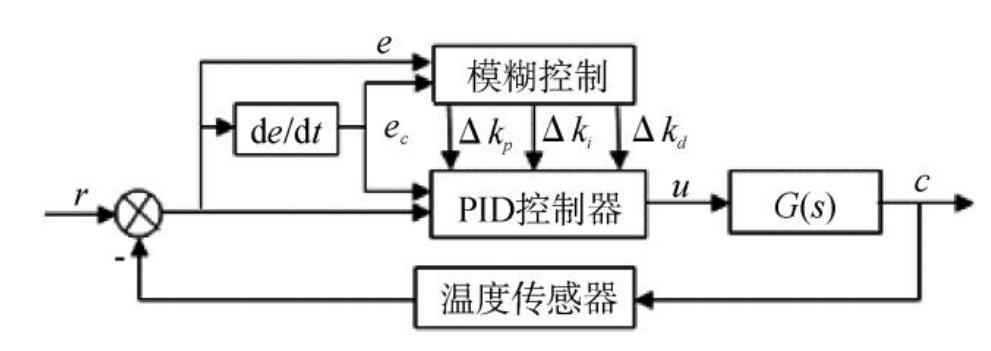
图8 模糊PID控制的控制原理图

2.2 模糊PID控制的仿真结果

模糊推理系统的建立




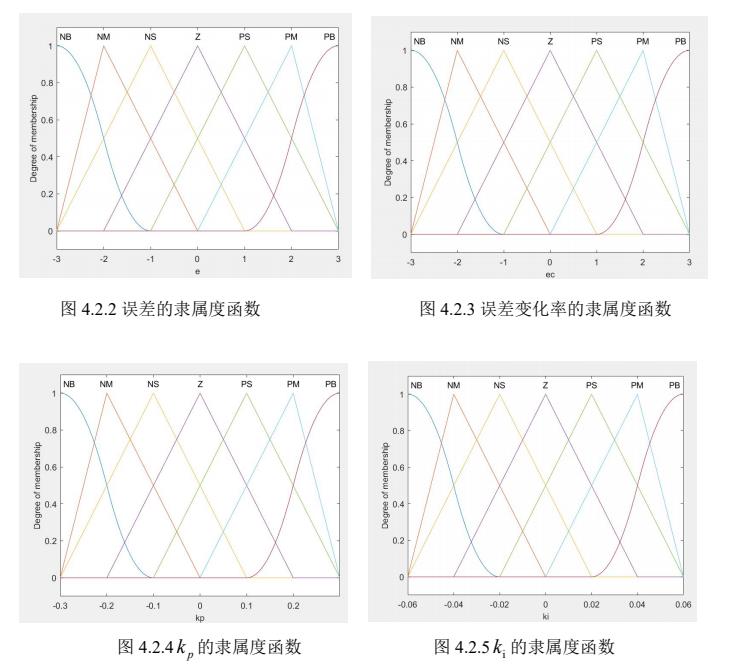
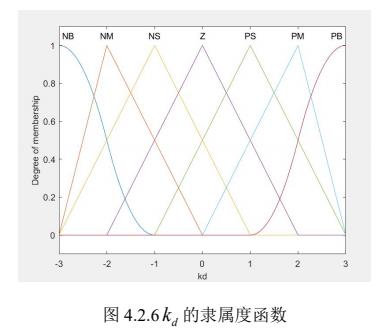
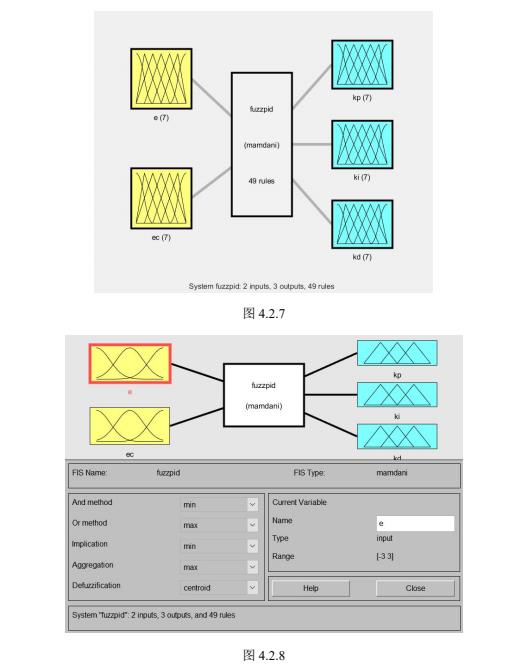
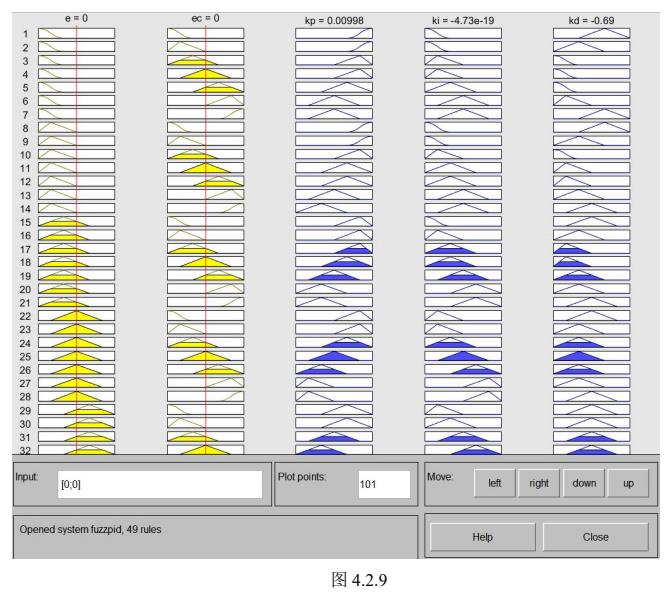
模糊PID的仿真结果

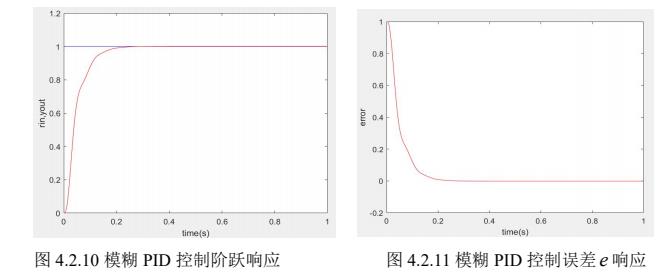
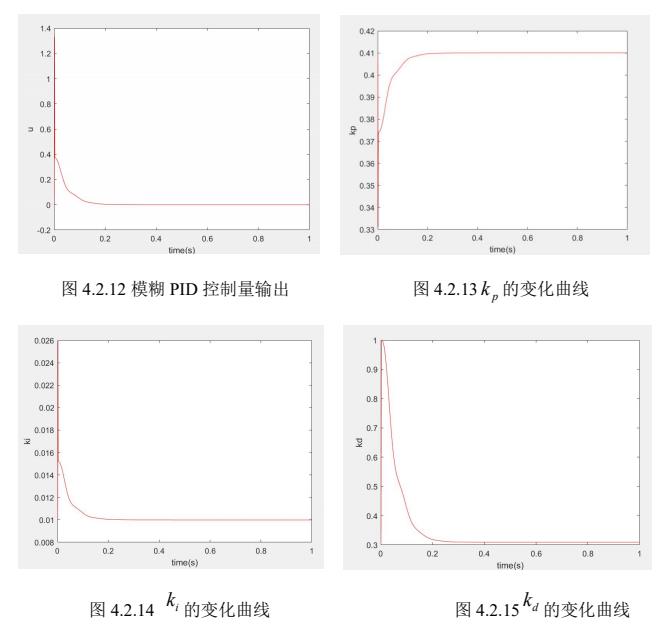
代码程序及仿真图

---

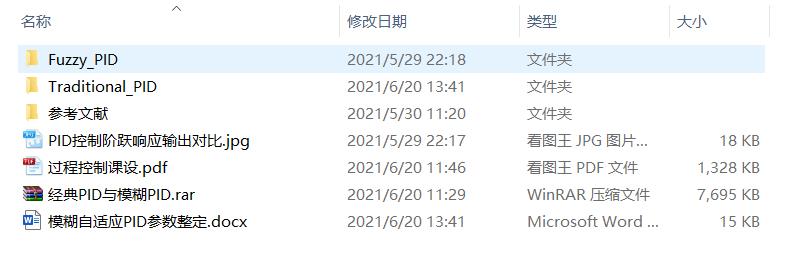
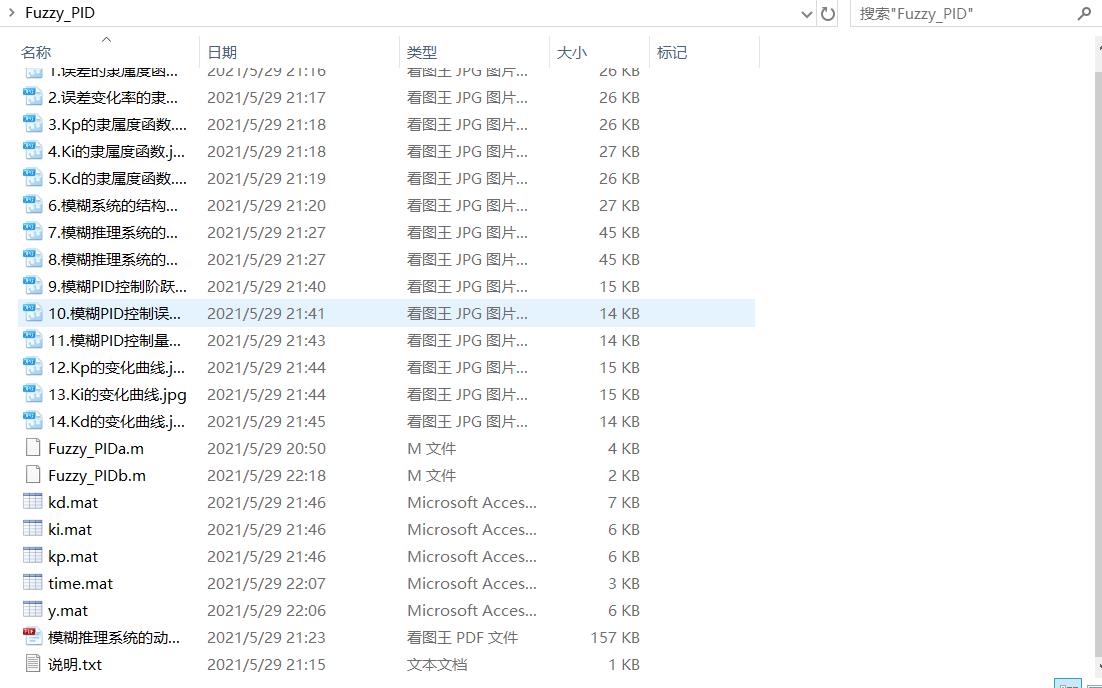
3仿真对比与分析

  将模糊PID控制与传统PID控制的输出响应进行对比，可得：

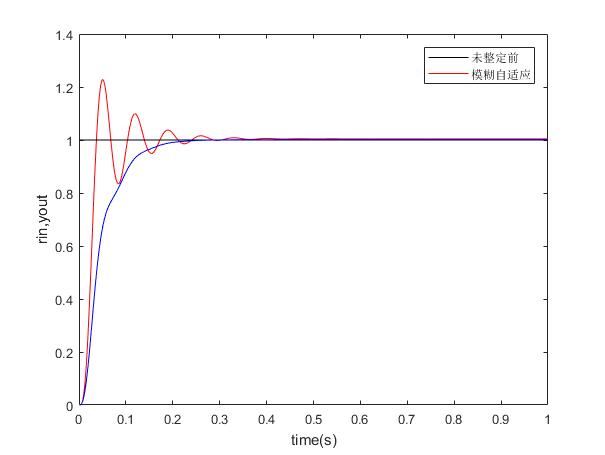
代码程序及仿真图

---