传送门
题目描述
It‘s Christmas time! PolandBall and his friends will be giving themselves gifts. There are n n Balls overall. Each Ball has someone for whom he should bring a present according to some permutation p, p{i}≠i for all i.
Unfortunately, Balls are quite clumsy. We know earlier that exactly k of them will forget to bring their gift. A Ball number i will get his present if the following two constraints will hold:
Ball number i will bring the present he should give. Ball x such that p{x}=i will bring his present. What is minimum and maximum possible number of kids who will not get their present if exactly k Balls will forget theirs?
思路
首先看到题目的时候,人肯定是懵逼的,完全不知道怎么做。
观察一段时间后,可以发现,如果从第i个人到这个人要送礼物给的第a{i}个人连一条有向线段,那么可以将整个图变成一堆闭合的环状结构,例如下面这个情况:
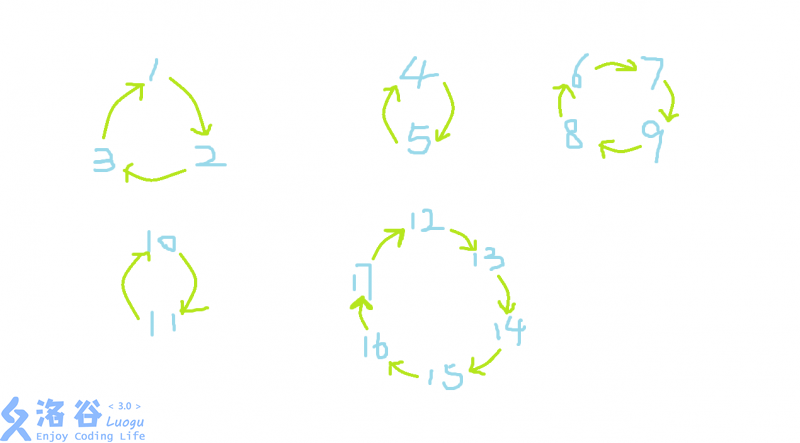
通过观察图片,可以得到这样的结论: 
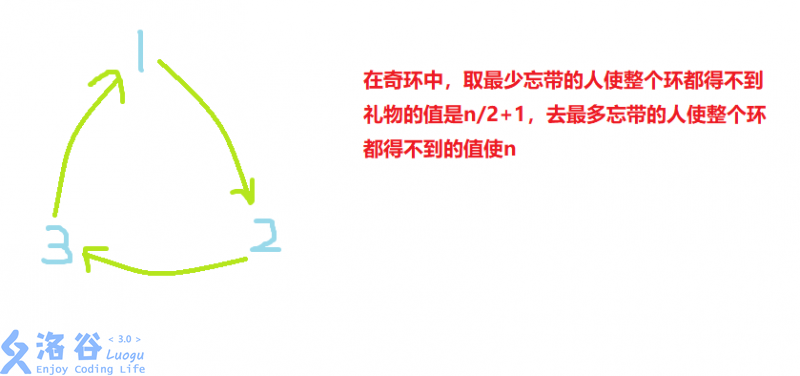
然后陷入懵逼循环,直到看了题解2333333
首先,题目让求最大值和最小值,那么就分别考虑
最大值时:
因为取不到礼物的人最多,所以可以想到这应该是一个贪心,贪心的策略是这样的:首先考虑取一个人而使两个人都没有礼物的情况,也就是说,如果a要给b礼物,那么选了a以后就绝对不会选b,此时我们从环入手,如果是偶环,那么很好办,只需要n/2个人就可以使n个人都没有礼物qwq,但是如果是奇环,按照我们的贪心策略,两个两个贪之后会有1个人剩余,那么我们先不去管这个人,继续去看别的环,如果能按原先的贪心策略取够k个人,那么我们就不去管之前剩下的人了。但是如果把所有的环都取了,还取不够k个人,那么就要回过头去考虑之前剩下的人,这样贪心就可以最大值贪出来。
int left=k; //剩余的人
int weipipei=0; //奇环未进行匹配的人
for(register int i=1;i<=cnt;i++){
if(huan[i]/2<=left){ //如果还能匹配整个环
left-=huan[i]/2;
maxans+=huan[i]/2*2;
}
else{ //如果剩下的人太少,不能匹配整个环
maxans+=left*2;
left=0;
}
if(huan[i]&1)weipipei++; //奇环,加剩下的人
}
maxans+=min(left,weipipei); //最后再加取最小值时:
显然每个环都取完是有最小,当然,不一定能保证刚好取一定数目的环可以使k个人刚好被取完,所以如果无法刚好取一定数目的环使人数总和为k时,剩下的人就要在余下的环中继续去取,这样的最小值为k+1,而如果刚好可以取一些环,使总和为k,那么最小值为k。
显然,这样分析完之后,就会发现这是一个多重背包,因为每种环的数目有限,要在所有种类的环中选一定数量的环,使其总和为k。 那么定义bool数组dp[i]为当选的人数为i是能否能用完整的还来表示,所以如果dp[k]的值为1,那么说明可以刚好凑出,答案为k,否则答案为k+1。
但是注意,这道题的数据范围很大,所以不能把一个种类的环拆分成单独的一个一个,然后做01背包,一定要用二进制优化,拆分为1,2,4,8,16……然后再做01背包,这样可以节省很多时间
int temp=0;
for(register int i=1;i<=cnt;i++){
if(huan[i]==huan[i-1])shu[temp]++;
else {
shu[++temp]++;
re[temp]=huan[i]; // tong ji shu ju
}
}这段代码是说,当时统计的时候是用cnt来表式第几个环,数组的值是环的大小,这样不好进行二进制优化,因为我们不知道每种大小的环有多少,所以shu数组表示环的多少,re数组表示环的大小。
cnt=0;
for(register int i=1;i<=temp;i++){
for(register int j=1;shu[i]>0;j<<=1){
int leftt=min(shu[i],j);
opt[++cnt]=leftt*re[i];
shu[i]-=leftt;
}
}进行二进制优化,opt数组记录二进制优化后,每种环拆开后的情况。
for(register int i=1;i<=cnt;i++){
for(register int j=k;j>=opt[i];j--){
if(dp[j-opt[i]])dp[j]=1;
}
}一个简单的背包23333
一个小细节
读入的时候要用scanf,不然会TLE qwq
附上完整代码(跟网上的题解几乎一摸一样qwq)
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[1000005],huan[1000005],shu[1000005],re[1000005],opt[1000005];
bool vis[1000005];
bool dp[1000005];
inline int cmp(int a,int b){
return a<b;
}
int dfs(int now,int from,int dep){
if(now==from)return dep;
else {
vis[now]=1;
dfs(a[now],from,dep+1);
}
}
int maxans=0;
int main(){
dp[0]=1;
int n,k;
cin>>n>>k;
for(register int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
int cnt=0;
for(register int i=1;i<=n;i++){
if(vis[i]==0){
huan[++cnt]=dfs(a[i],i,1);
}
}
sort(huan+1,huan+cnt+1,cmp);
// qiu zui da zhi ------ tan xin
int left=k;
int weipipei=0;
for(register int i=1;i<=cnt;i++){
if(huan[i]/2<=left){
left-=huan[i]/2;
maxans+=huan[i]/2*2;
}
else{
maxans+=left*2;
left=0;
}
if(huan[i]&1)weipipei++;
}
maxans+=min(left,weipipei);
// qiu zui xiao zhi ------duo chong bei bao
int temp=0;
for(register int i=1;i<=cnt;i++){
if(huan[i]==huan[i-1])shu[temp]++;
else {
shu[++temp]++;
re[temp]=huan[i]; // tong ji shu ju
}
}
cnt=0;
for(register int i=1;i<=temp;i++){
for(register int j=1;shu[i]>0;j<<=1){
int leftt=min(shu[i],j);
opt[++cnt]=leftt*re[i];
shu[i]-=leftt;
}
}
for(register int i=1;i<=cnt;i++){
for(register int j=k;j>=opt[i];j--){
if(dp[j-opt[i]])dp[j]=1;
}
}
int minans=k;
if(!dp[k])minans++;
cout<<minans<<‘ ‘<<maxans<<endl;
}