Schmidt正交化与Schur定理求正交的区别是？
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Schmidt正交化与Schur定理求正交的区别是？相关的知识，希望对你有一定的参考价值。
史密斯正交化与Schur定理求正交的区别是？
参考技术A Gram-Schmidt正交化相当于QR分解的一种构造算法A=QR，其中A、Q、R的阶数分别是mxn、mxn、nxn，Q是酉阵，R是上三角阵
当然一般来讲正交化还需要A满秩的条件，不然需要稍微调整一下。
而Schur分解是一种关于特征值的分解A=QTQ^H，其中Q是酉阵，T是上三角阵。
即便A是方阵也是有一定区别的
QR分解是一种单侧分解，并且可以在有限步运算内构造性地得到；
而Schur分解是双侧分解，本质上就是求特征值，一般不能在有限步四则运算和开方内完成，其存在性是靠代数基本定理非构造性地保证的。
现代信号处理 04 - 正交化与维纳滤波
正交化与维纳滤波
1. 线性估计与正交性之间的联系
1.1 相关运算的本质
我们先来回顾一下我们的线性估计问题。
假设有两个随机变量Z和Y，我们希望通过线性估计的方法让Z来逼近Y，也就是
Z , Y Z − > Y Z,Y \\\\ Z->Y Z,YZ−>Y
我们的优化条件是估计量与真值的均方误差最小，即
m i n E ( Y − α Z ) 2 min E(Y - \\alpha Z)^2 minE(Y−αZ)2
求导可得
∇ α = 2 ∗ E ( Z ∗ ( Y − α Z ) ) = 0 \\nabla _ \\alpha = 2*E(Z*(Y - \\alpha Z))=0 ∇α=2∗E(Z∗(Y−αZ))=0
最终可以得到
α = E ( Z Y ) E ( Z 2 ) \\alpha = \\frac{E(ZY)}{E(Z^2)} α=E(Z2)E(ZY)
我们得到这个结论的时候，有一点是值得好好体味一下的。
就是求导条件
∇ α = 2 ∗ E ( Z ∗ ( Y − α Z ) ) = 0 \\nabla _ \\alpha = 2*E(Z*(Y - \\alpha Z))=0 ∇α=2∗E(Z∗(Y−αZ))=0
我们注意到这是Z与Y的残差之间的相关运算等于0
相关运算本质上是在计算向量的内积。而且我们知道，内积是与向量夹角有关系的。因此相关运算的大小实际上代表的是向量的角度
C o s ( Z 1 , Z 2 ) = < Z 1 , Z 2 > ∣ ∣ Z 1 ∣ ∣ ∗ ∣ ∣ Z 2 ∣ ∣ Cos(Z_1,Z_2) = \\frac{<Z_1,Z_2>}{||Z_1||*||Z_2||} Cos(Z1,Z2)=∣∣Z1∣∣∗∣∣Z2∣∣<Z1,Z2>
我们抛开底下的取模运算不管，因为这实际上就是归一化。相关运算和向量的角度是直接相关的。
因此两个随机变量的夹角就是两个随机变量的相关系数。
如果两个向量的相关为0，就说明这个夹角是90度，也就是随机变量是正交的。所以，我们发现，我们在取最优的过程中，实际上就是采样值与估计残差之间的相关，如果二者不相关，就意味着达到了最优。从而说明了，最优性是从正交性提取出来的，就是要计算我们估计的原材料和估计的残差之间的相关
1.2 几何意义下的线性估计
我们来从几何意义下观察一下，求线性估计在几何上是在做什么
1.2.1 单变量估计
我们先从单变量开始
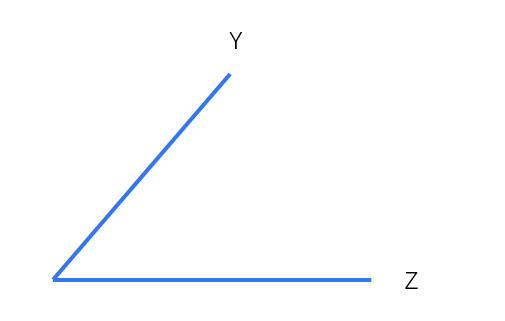
我们假设有随机变量Y和Z，我们用Z来估计Y。我们从图中可以看出来，实际上我们就是要估计一条向量，到Y的距离最短。这个向量的终点就是Y到Z的垂线的垂足。
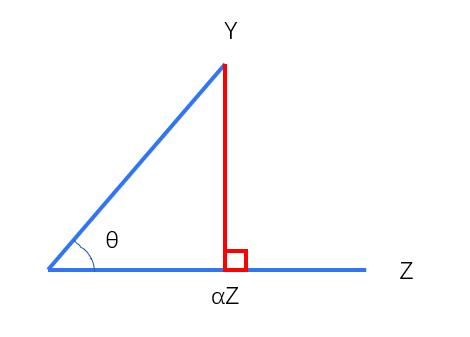
我们来求一下投影的长度
∣ ∣ Y ∣ ∣ ∗ C o s θ = ∣ ∣ Y ∣ ∣ ∗ E ( Y X ) ∣ ∣ Y ∣ ∣ ∗ ∣ ∣ Z ∣ ∣ = E ( Y X ) ∣ ∣ Z ∣ ∣ ||Y||*Cos\\theta = ||Y||*\\frac{E(YX)}{||Y||* ||Z||} = \\frac{E(YX)}{||Z||} ∣∣Y∣∣∗Cosθ=∣∣Y∣∣∗∣∣Y∣∣∗∣∣Z∣∣E(YX)=∣∣Z∣∣E(YX)
再把方向加上
α Z = ∣ ∣ Y ∣ ∣ ∗ C o s θ ∗ Z ∣ ∣ Z ∣ ∣ = E ( Y X ) ∣ ∣ Z ∣ ∣ 2 Z \\alpha Z = ||Y||*Cos\\theta*\\frac{Z}{||Z||} = \\frac{E(YX)}{||Z||^2}Z αZ=∣∣Y∣∣∗Cosθ∗∣∣Z∣∣Z=∣∣Z∣∣2E(YX)Z
可以得到α
α = E ( Y X ) ∣ ∣ Z ∣ ∣ 2 \\alpha = \\frac{E(YX)}{||Z||^2} α=∣∣Z∣∣2E(YX)
我们在几何上寻找最优解，实际上是在找正交投影
因此正交性是我们最优线性估计的关键,估计的残差要与估计的原材料正交
1.2.2 多变量估计
我们把问题推广到多变量上
我们假设有一组随机变量
Z 1 , . . . , Z k Z_1,...,Z_k Z1,...,Zk
我们希望用这组随机变量去估计Y，也就是
Y < − ( Z 1 , . . . , Z k ) T Y <-(Z_1,...,Z_k)^T Y<−(Z1,...,Zk)T
估计条件为
m i n E ( Y − ( α 1 ∗ Z 1 + α 2 ∗ Z 2 + . . . + α k ∗ Z k ) ) 2 minE(Y- (\\alpha_1*Z_1+\\alpha_2*Z_2+...+\\alpha_k*Z_k))^2 minE(Y−(α1∗Z1+α2∗Z2+...+αk∗Zk))2
对任意一个αk求导
− 2 E ( Z k ∗ ( Y − ( α 1 ∗ Z 1 + α 2 ∗ Z 2 + . . . + α k ∗ Z k ) ) ) = 0 -2E(Z_k*(Y- (\\alpha_1*Z_1+\\alpha_2*Z_2+...+\\alpha_k*Z_k))) = 0 −2E(Zk∗(Y−(α1∗Z1+α2∗Z2+...+αk∗Zk)))=0
我们可以看到残差与任意一个估计的原材料都是正交的
我们继续从几何层面进行分析。就是Z构成了一个线性子空间，在线性子空间离找距离Y最近的点，也就是Y的投影点
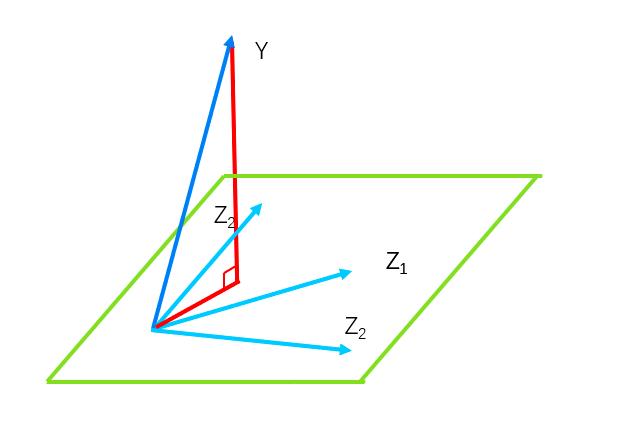
这个被称为正交性原理
1.3 正交性原理
实际上，求正交性等价于求最优性，下面我们用数学公式的形式进行严格描述
假定H是一个线性空间，Z是属于H空间的一个向量。H0是H的一个子空间，如果H0中存在一个向量x0，满足与Z的距离最短，当且仅当残差与任何一个x都正交的时候成立，也就是残差正交与H0
Z
∈
H
H
0
⊂
H
x
0
∈
H
0
∣
∣
x
0
−
Z
∣
∣
=
m
i
n
∣
∣
x
−
Z
∣
∣
⟺
<
Z
−
x
0
,
x
>
=
0
以上是关于Schmidt正交化与Schur定理求正交的区别是？的主要内容，如果未能解决你的问题，请参考以下文章 利用Gram—Schmidt正交化方法，求[-1, 1]上带权 的正交多项式系，并列出它的性质（正交性）