UnityUnity 欧拉角四元数万向节死锁四元数转轴角
Posted 是嘟嘟啊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了UnityUnity 欧拉角四元数万向节死锁四元数转轴角相关的知识,希望对你有一定的参考价值。
文章目录
欧拉角(Euler)
什么是欧拉角?百科上是这样解释的:用来确定定点转动刚体位置的3个一组独立角参量,由章动角θ、旋进角(即进动角)ψ和自转角φ组成,为欧拉首先提出而得名。

很难理解吧?其实我们没有必要把欧拉角想得太复杂。
对于开发者来说,欧拉角就是用一个Vector3变量来记录物体沿着x、y、z轴的旋转。注意,虽然这是一个Vector3变量,但它并不是向量,这个变量的x、y、z三个分量是用来描述旋转的。
欧拉角特点:
- 使用3个角度来保存方位。
- x 与 z沿自身坐标旋转,y 沿世界坐标旋转。
- API:Vector3 eulerAngle = this.transform.eulerAngles;
万向节
万向节,也叫平衡环架(Gimbal),具有枢纽的装置,使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架,则可使架在最内的环架的物体维持旋转轴不变。常常应用于船上的陀螺仪、罗盘、饮料杯架等。

在飞行器的航行中,进行XYZ三个方向旋转的旋转有专业的术语,见下图:

沿着机身右方轴(Unity中的+X)进行旋转,称为pitch,中文叫俯仰。
沿着机头上方轴(Unity中的+Y)进行旋转,称为Yaw,中文叫偏航。
沿着机头前方轴(Unity中的+Z)进行旋转,称为Roll,中文叫桶滚。
欧拉角旋转特性
欧拉角的旋转就是沿着万向节的轴旋转的。目前人类最常用也最容易理解的方式是先沿着X轴旋转,再沿着Y轴旋转,最后沿着Z轴旋转,最后达到目标旋转角度。如下图所示:
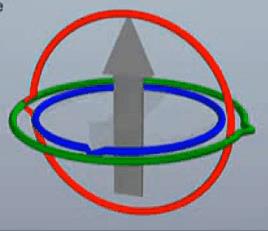
这时候可能就有人会有疑问了,为什么不能三个轴同时旋转呢?
实际上,如果三个轴同时旋转,将会无法达到你预期的旋转效果。为什么呢?因为物体是一个整体,当某一个轴进行旋转时,其他的轴是跟着物体一起动的,如果还是按照原来的旋转角度旋转则会随着其他轴的转动形成偏移,如下图所示:

我们想要的其实只是让箭头指向我们,但三个轴同时旋转却使这个旋转轨迹划出了一个不应该有的弧线。
所以我们要了解的是,欧拉旋转是一定要有顺序的。这样的问题其实是无法避免的,但是我们可以根据物体的旋转情况对此进行优化,这个优化的方法就是给三个轴指定一个新的层级顺序。

当然这并不是真正的解决了问题,只是尽量避免了问题而已。欧拉角的问题是无法彻底解决的,
欧拉角优点
- 仅使用三个数字表达方位,占用空间小。
- 沿坐标轴旋转的单位为角度,符合人类思考方式。
- 任意三个数字都是合法的,不存在不合法的欧拉角。
欧拉角缺点
方位的表达方式不唯一
对于一个方位,存在多个欧拉角描述,因此无法判断多个欧拉角代表的唯一是否相同。
例如:
- 角度 0, 5, 0 与角度 0, 365, 0
- 角度 0, -5, 0 与角度 0, 355, 0
- 角度 250, 0, 0 与角度 290, 180, 180
为了保证任意方位都只有独一无二的表示,Unity引擎限制了角度范围,即沿x轴旋转限制在 -90 ~ 90 之间,沿 y 与 z 轴旋转限制在 0 ~ 360 之间。
万向节锁(Gimbal Lock)
当物体沿 x 轴旋转
±
90
°
\\ \\plusmn 90°
±90° ,自身坐标系z轴与世界坐标系y轴将重合,此时再沿y轴或z轴旋转时,将会失去一个自由度。

Unity的优化方案:在万向节死锁的情况下,规定沿z轴完成绕竖直轴的全部旋转,即此时y轴旋转为0。
关于万向节锁的讲解视频:https://v.youku.com/v_show/id_XNjk1MTkzMTM2.html#paction
在使用欧拉旋转的情况下,万向节锁的情况是无法避免的,为了更好的表示旋转,Unity引入了四元数的概念。
四元数(Quaternion)
四元数在3D图形学中代表旋转,由一个三维向量 / [ x , y , z ] / [x, y, z] /[x,y,z] 和一个标量 / w / w /w 组成。
旋转轴为
V
V
V ,旋转弧度为
θ
\\theta
θ ,若使用四元数表示,则四个分量为:
x
=
S
i
n
(
θ
/
2
)
∗
V
.
x
y
=
S
i
n
(
θ
/
2
)
∗
V
.
y
z
=
S
i
n
(
θ
/
2
)
∗
V
.
z
w
=
C
o
s
(
θ
/
2
)
x = Sin(\\theta / 2) * V.x \\\\ y = Sin(\\theta / 2) * V.y \\\\ z = Sin(\\theta / 2) * V.z \\\\ w = Cos(\\theta / 2)
x=Sin(θ/2)∗V.xy=Sin(θ/2)∗V.yz=Sin(θ/2)∗V.zw=Cos(θ/2)
四个分量的值都在 -1 到 1 之间。
几何应用:四元数与向量相乘,可以实现向量的旋转。
代码:
// 获取四元数
Quaternion qt = this.transform.rotation;
// 使用四元数做旋转
this.transform.rotation = Quaternion.Euler(0, 50, 0);
// 或者调用Rotation方法实现旋转
this.transform.Rotation(0, 50, 0);
四元数旋转角度相加需要用 * 乘法,而不是加法。
四元数转轴角
Transform 中的 rotation 使用的是四元数,有时我们需要获取 Transform 沿某一个轴旋转的角度,此时可以用下面的代码进行计算:
Quaternion q = transform.rotation;
// 计算X轴旋转角度
float angleX = 0;
float siny_cosp1 = 2 * (q.w * q.x + q.z * q.y);
float cosy_cosp1 = 1 - 2 * (q.y * q.y + q.x * q.x);
float radian1 = Mathf.Atan2(siny_cosp1, cosy_cosp1); // 求出弧度
angleX = radian1 * Mathf.Rad2Deg; // 转化角度
Debug.Log("=============" + angleX);
// 计算Z轴旋转角度
float angleZ = 0;
float siny_cosp2 = 2 * (q.w * q.z + q.x * q.y);
float cosy_cosp2 = 1 -2 * (q.y * q.y + q.z * q.z);
float radian2 = Mathf.Atan2(siny_cosp2, cosy_cosp2); // 求出弧度
angleZ = radian2 * Mathf.Rad2Deg; // 转化角度
Debug.Log("=============" + angleZ);
上述方法适用于物体只在一个轴上做了旋转的情况,Y轴的计算方法以此类推。
四元数优点
避免万向节死锁,完全沿自身轴(而不是全局轴)旋转。
四元数缺点
难于使用,且存在不合法的数值。
Quaternion类
Unity中提供了Quaternion类来处理四元数相关操作,该类的使用方法可以参考我的另外一篇文章:【Unity】Unity常用类:向量Vector3、四元数Quaternion
本文万向节部分内容参考了塞北烟云大神的文章,地址如下:https://www.jianshu.com/p/9f45e91a2391
更多内容请查看总目录【Unity】Unity学习笔记目录整理
欧拉角四元数和矩阵的对比(转)
三维空间的旋转可以用欧拉角,旋转矩阵,轴-角,四元数,双四元数来表示,本文主要总结这些表示方法的优缺点。
一. 欧拉角(Euler-Angles)
1.1 介绍
欧拉角包括3个旋转,根据这3个旋转来指定一个刚体的朝向。这3个旋转分别绕x轴,y轴和z轴,分别称为Pitch,Yaw和Roll,如下图所示。欧拉角可以表示成z-x-z,x-y-x,z-y-z等形式,旋转的顺序影响结果。
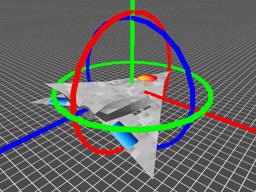 Pitch
Pitch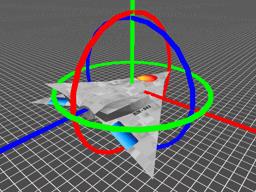 Yaw
Yaw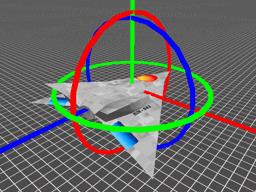 Roll
Roll
图1. 欧拉角的表示
欧拉角很重要的一个优点就是直观,容易理解。
欧拉角主要有下面几个缺点:
(1) 欧拉角是不可传递的,旋转的顺序影响旋转的结果,不同的应用又可能使用不同的旋转顺序,旋转顺序无法统一;
(2) 3个旋转的角度可以不受限制,即可以是10000度,也可以是-1500度;
(3) 可能造成万向节死锁(Gimbal Lock)。
1.2 平万向节死锁
当两个环发生重叠的时候,就有丢失了一个自由度,如图2所示。对万向节死锁可以参考【1】【2】【3】,特别是【1】提供的视频,对知识点的介绍非常的形象生动。也正是由于锁的存在,无法使用欧拉角实现球面平滑的插值。

图2. 万向节死锁
二. 旋转矩阵
用3*3的矩阵,可以表示三维空间中所有的旋转,设θ表示沿着轴的方向望去时,方向是顺时针的旋转角度。则绕着X轴、Y轴、Z轴旋转θ角,对应的旋转矩阵表示如下所示:
X=⎛⎝⎜1 0 0 0cosθsinθ0−sinθcosθ⎞⎠⎟ Y=⎛⎝⎜cosθ0−sinθ010sinθ0cosθ⎞⎠⎟ Z=⎛⎝⎜cosθsinθ0−sinθcosθ0001⎞⎠⎟
旋转矩阵支持传递性,使用起来很简单方便,但是存在下面一些缺点:
(1) 浪费内存,至少需要12个参数,来表示一个6个自由度的结构;
(2) 可能就引入不该有的缩放(Scaling)和错切(Sheering)
(3) 矩阵插值的实现难度很大;
(4) 不直观。
三. 轴-角度
绕着单位长度的轴旋转某个角度,使用组合对(n⃗ ,θ)。
该方向很直观,避免了欧拉角使用时的万向节死锁;但是实现多个旋转的组合时,比较困难;不能简单的通过对4个元素的线性插值来实现轴-角度的插值,会引起错误。
四. 四元数
参考《四元数》,也可以参考【5】【6】【7】,这里只简单的描述下该方法的优缺点。
它的缺点就是很不直观,理解起来较费劲。但是存在很多优点:
(1) 更健壮,不会出现欧拉角中出现的万向节死锁。
(2) 更高效,花费更少的空间和时间;当使用有限的精度对矩阵进行大量的操作,就会发生漂移(Drift),实数的四舍五入就会不断累积到矩阵中。由于漂移的存在,旋转的操作就可能发生错误,所以要对矩阵进行归一化操作,重置矩阵,这是很费时的操作。四元数只有4个值,而矩阵有9个,它经历的漂移作用就小,而且归一化时间就更少。
(3) 使用起来很简单
参考
【1】 http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html
【2】 http://www.cnblogs.com/soroman/archive/2008/03/24/1118996.html
【3】 http://www.cnitblog.com/luckydmz/archive/2010/09/07/68674.aspx
【4】 Kenwright, Ben. "A Beginners Guide to Dual-Quaternions."
【5】 http://www.cprogramming.com/tutorial/3d/quaternions.html
【6】 http://isg.cs.tcd.ie/projects/DualQuaternions/
【7】 http://www.gamedev.net/page/resources/_/technical/math-and-physics/quaternion-powers-r1095
以上是关于UnityUnity 欧拉角四元数万向节死锁四元数转轴角的主要内容,如果未能解决你的问题,请参考以下文章