「解析」牛客网-华为机考企业真题 41-60
Posted ViatorSun
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了「解析」牛客网-华为机考企业真题 41-60相关的知识,希望对你有一定的参考价值。
又是一年春招时,有幸收到华为自动驾驶算法岗,之前刷题不多,在此汇总下牛客网的真题,主要采用Python编写,个人觉得语言只是实现工具而已,并不是很关键,Python简洁易懂,更加适合算法工程师快速验证idear,避免重复造轮子的繁琐,希望对看合集的你有些许帮助!
- 「解析」牛客网-华为机考企业真题 1-20
- 「解析」牛客网-华为机考企业真题 21-40
- 「解析」牛客网-华为机考企业真题 41-60
- 「解析」牛客网-华为机考企业真题 61-80
- 「解析」牛客网-华为机考企业真题 81-108
文章目录
- HJ41 称砝码
- ★★★ HJ42 学英语
- HJ43 迷宫问题
- ★★★ HJ44 Sudoku
- HJ45 名字的漂亮度
- HJ46 截取字符串
- HJ48 从单向链表中删除指定值的节点
- HJ50 四则运算
- HJ51 输出单向链表中倒数第k个结点
- HJ52 计算字符串的编辑距离
- HJ53 杨辉三角的变形
- HJ54 表达式求值
- HJ55 挑7
- HJ56 完全数计算
- HJ57 高精度整数加法
- HJ58 输入n个整数,输出其中最小的k个
- HJ59 找出字符串中第一个只出现一次的字符
- HJ60 查找组成一个偶数最接近的两个素数
HJ41 称砝码

每次加一块砝码,得到所有组合,使用set去重。这是一种思路,我看很大一部分同学都是使用n种不同砝码进行组合,那样的话时间复杂度稍微低一点,实际看个人觉得哪种方式更好理解。
while True:
try:
n = int(input())
m = input().split(" ")
x = input().split(" ")
# mx为所有砝码,比如示例mx为[1, 1, 2]
mx, l = [], 0
for i in range(n):
mx.extend([int(m[i])] * int(x[i]))
for i in mx:
# 每次加一块砝码,使用union(并集)得到新去重的组合,如果不使用union则稍微麻烦一点,需要考虑循环中改变set
l = l.union(i+j for j in l)
print(len(l))
except:
break
★★★ HJ42 学英语
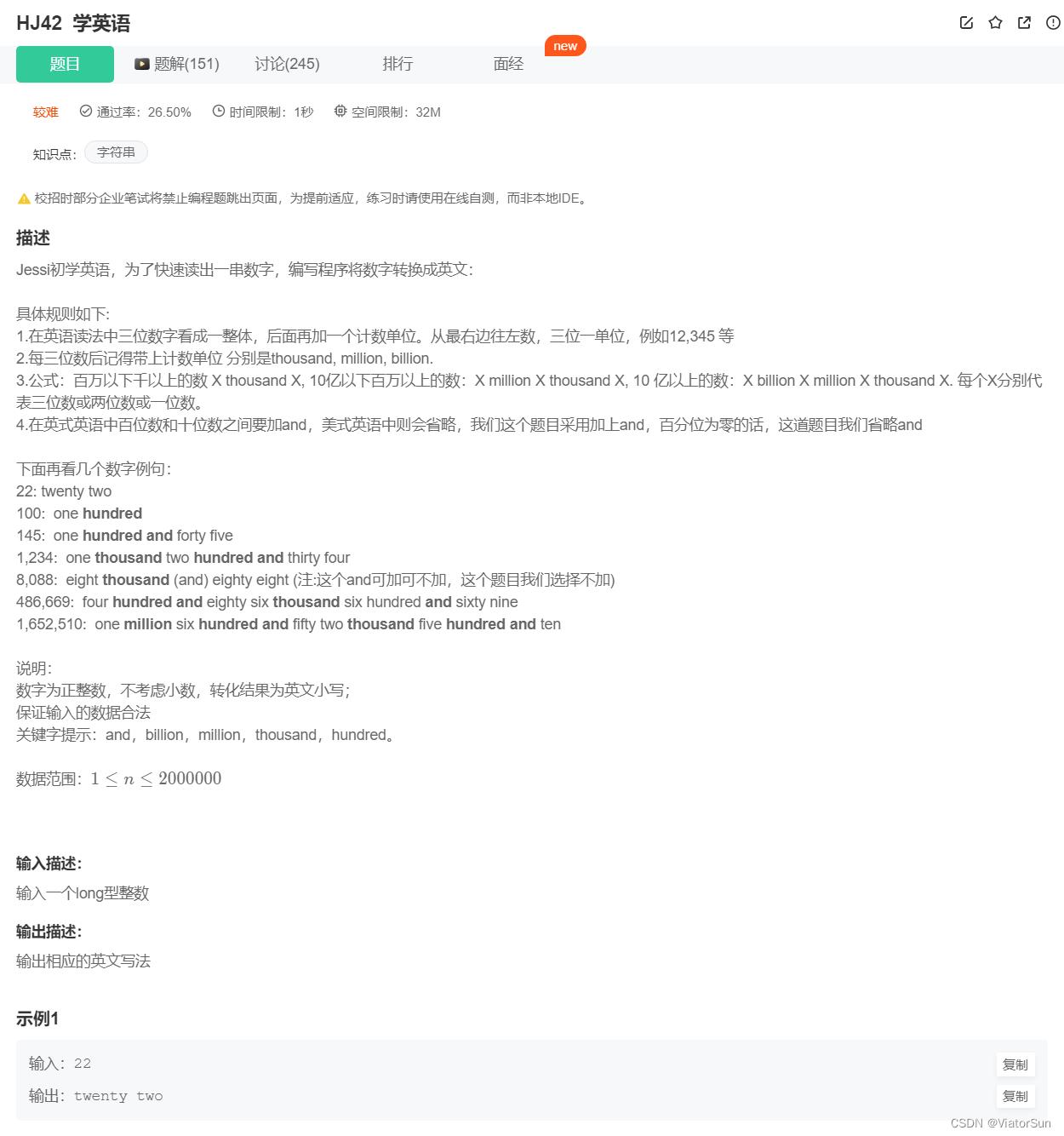
num1 = ['zero','one','two','three','four','five','six',
'seven','eight','nine','ten','eleven','twelve',
'thirteen','fourteen','fifteen','sixteen',
'seventeen','eighteen','nineteen']
num2 = [0,0,'twenty','thirty','forty','fifty','sixty',
'seventy','eighty','ninety']
# 100以内转英文
def n2w(n):
if n > 0:
if n < 20:
word.append(num1[n])
else:
word.append(num2[n//10])
if n%10 != 0:
word.append(num1[n%10])
# 1000以内转英文
def hun(n):
if n >= 100:
word.append(num1[n//100])
word.append('hundred')
if n % 100 != 0:
word.append('and')
n2w(n%100)
while True:
try:
n = int(input())
except:
break
else:
word = []
a = n % 1000 # 个十百位
b = (n//1000) % 1000 # 个十百千
c = (n//1000000) % 1000 #个十百m
d = n // 1000000000 # 个十百b
if d > 0:
hun(d)
word.append('billion')
if c > 0 :
hun(c)
word.append('million')
if b > 0:
hun(b)
word.append('thousand')
if a > 0 :
hun(a)
print(' '.join(word))
HJ43 迷宫问题

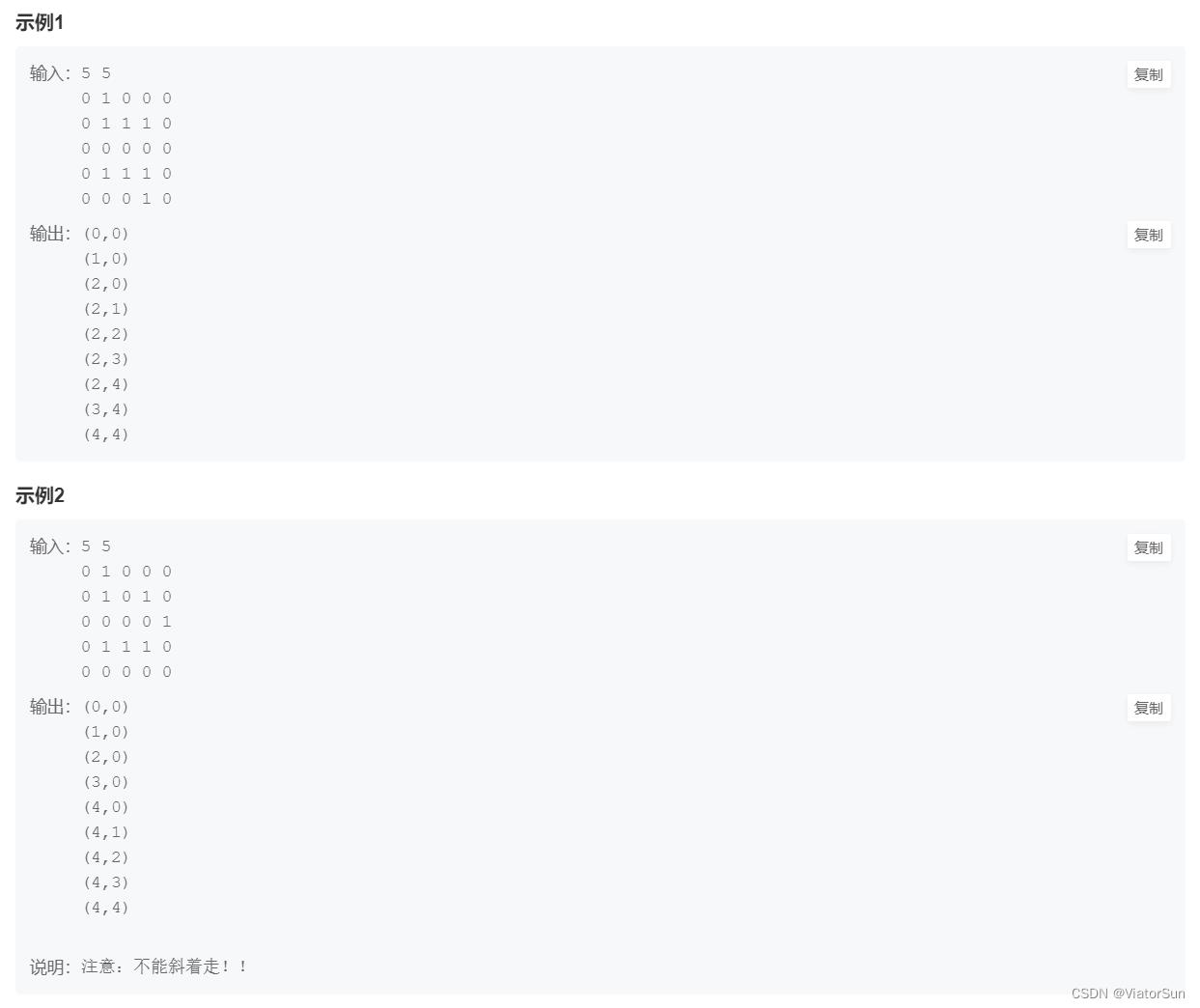
while True:
try:
m, n = list(map(int, input().split()))
maze = []
for _ in range(m):
maze.append(list(map(int, input().split())))
def walk(i, j, pos=[(0, 0)]):
if j+1 < n and maze[i][j+1] == 0: # 向右
if (i, j+1) not in pos:
walk(i, j+1, pos + [(i, j+1)])
if j-1 >= 0 and maze[i][j-1] == 0: # 向左
if (i, j-1) not in pos:
walk(i, j-1, pos + [(i, j-1)])
if i+1 < m and maze[i+1][j] == 0: # 向下
if (i+1, j) not in pos:
walk(i+1, j, pos + [(i+1, j)])
if i-1 >= 0 and maze[i-1][j] == 0: # 向上
if (i-1, j) not in pos:
walk(i-1, j, pos + [(i-1, j)])
if (i, j) == (m-1, n-1): # 到达出口
for p in pos:
print('(' + str(p[0]) + ',' + str(p[1]) + ')')
walk(0, 0)
except:
break
★★★ HJ44 Sudoku



def check(sudoku,i,j): #判断这个数填入数独的i,j位置是否合理
for k in range(9):
if(sudoku[i][k] == sudoku[i][j]) and (k != j): #若是这一列有重复的数据,认为这个数非法
return False
for k in range(9):
if(sudoku[k][j] == sudoku[i][j]) and (k != i): #若是这一行有重复的数据,认为这个数非法
return False
m = 3*(i // 3) #m,n分别是i,j位置所在的3*3格子的最左上角的位置
n = 3*(j // 3)
for k in range(3):
for z in range(3):
if(sudoku[m+k][n+z] == sudoku[i][j]) and ((m+k) != i) and ((n+z) != j): #判断所在3*3格子是否有重复的数据
return False
return True #若都没有,那么认为这个数在重复上面没有问题
def find_sudoku(sudoku):
for i in range(9):
for j in range(9):
if(sudoku[i][j] == 0): #若是找到为0的
for t in range(1,10): #在这个位置依次填入1-9尝试
sudoku[i][j] = t
if(check(sudoku,i,j)) and (find_sudoku(sudoku)): #若是满足数独要求,而且填完这个数之后的0也能被成功填写
return True #认为成功
sudoku[i][j] = 0 #如果1-9都不行认为是之前填的数不合适,恢复这次填的数
return False #返回之前一个false
return True 走到这一步认为所有的空都被填满,返回成功
while True:
try:
sudoku = []
sudoku_index = []
for i in range(9):
a = list(map(int,input().split()))
sudoku.append(a) #将数独输入
find_sudoku(sudoku)
for i in range(9):
print(*sudoku[i])
except:
break
HJ45 名字的漂亮度

while True:
try:
#获取输入的单词数量
N = int(input())
while N:
#获取输入的单词
data = input()
#去重存入字典
d =
for word in data:
if word not in d:
d[word] = 1
else:
d[word] = d[word] + 1
d1 = sorted(d.values() ,reverse=True)
ans = 0
m = 0
for word in d1:
ans = ans + (26-m)*word
m = m + 1
print(ans)
N = N - 1
except:
break
HJ46 截取字符串

while True:
try:
str_input = input()
k = int(input())
print(str_input[:k])
except:
break
HJ48 从单向链表中删除指定值的节点
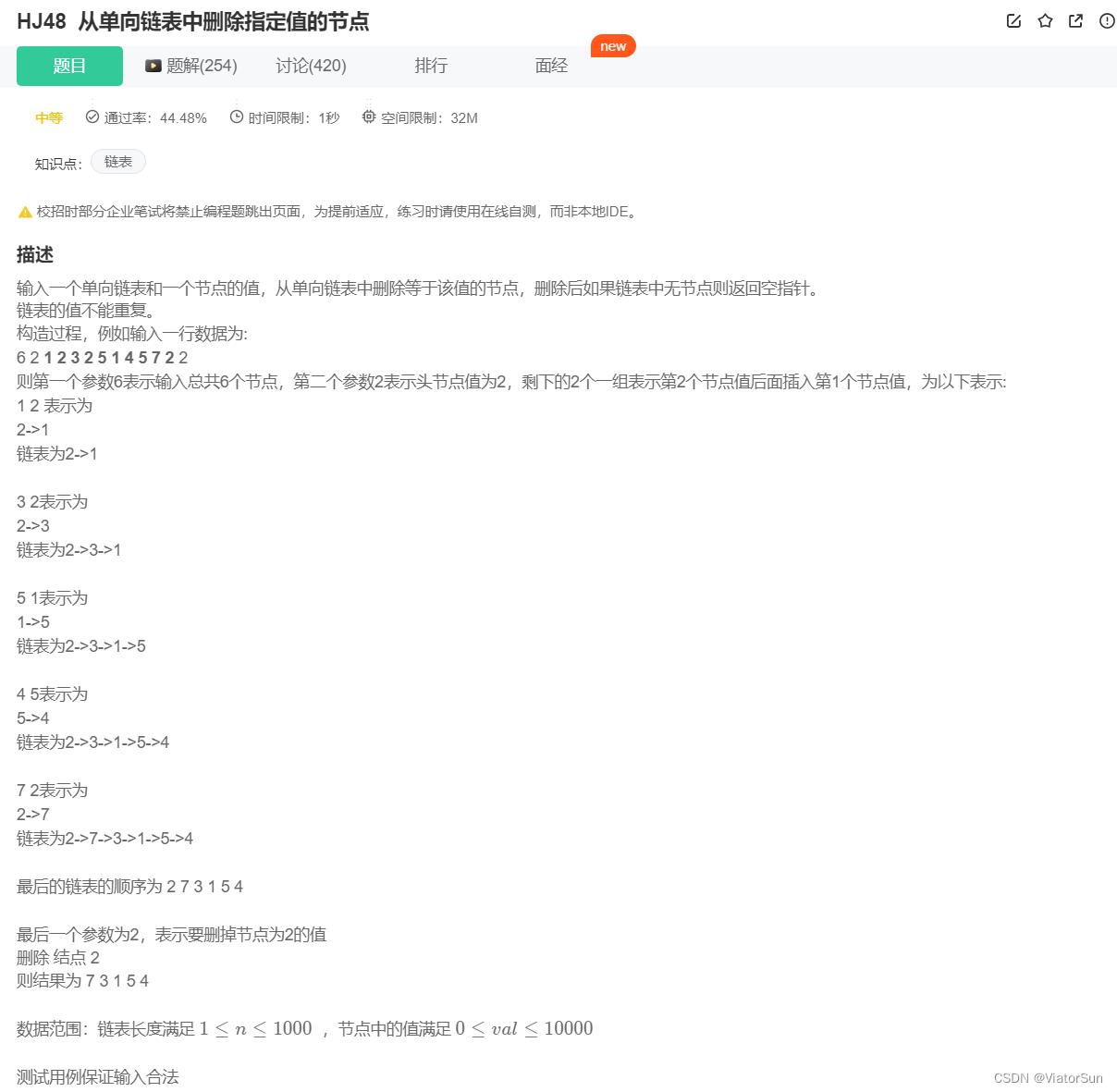

while True:
try:
num = list(map(int,input().split()))
n = len(num)
new = []
for i in range(2,n-1,2):
if num[i+1] not in new: #没有就追加
new.append(num[i+1])
new.append(num[i])
else: #有就插队
ind = new.index(num[i+1])
new.insert(ind+1,num[i])
#循环删除节点
try:
while True:
new.remove(num[-1])
except:
pass
#输出
new = [str(x) for x in new]
print(' '.join(new))
except:
break
HJ50 四则运算

while True:
try:
s=input()
s=s.replace('', '(')
s=s.replace("",")")
s=s.replace("[","(")
s=s.replace("]",")")
print(int(eval(s)))
except:
break
HJ51 输出单向链表中倒数第k个结点
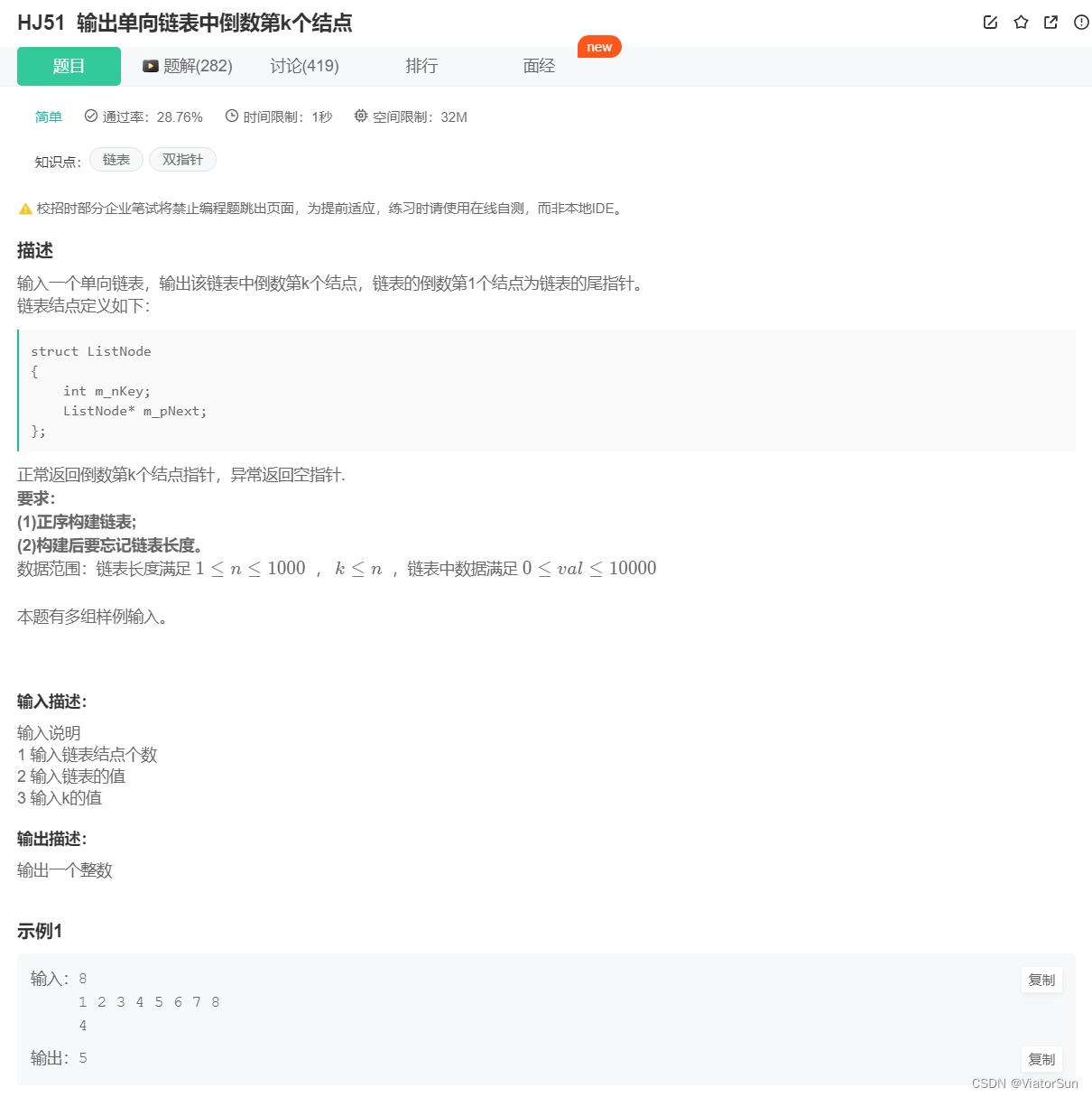
链表做法,直接逆向遍历
class Node(object):
def __init__(self, val=0):
self.val = val
self.next = None
while True:
try:
head = Node()
count, num_list, k = int(input()), list(map(int, input().split())), int(input())
while k:
head.next = Node(num_list.pop())
head = head.next
k -= 1
print(head.val)
except EOFError:
break
HJ52 计算字符串的编辑距离

#动态规划经典题目
#nowcoder不能导入numpy模块,只能手工创建二维数组
#重点注意二维数据的创建方法,重点注意其横竖坐标,注意注意
#dp = [[1 for i in range(n+1)] for j in range(m+1)],横坐标是 n, 竖坐标是m
while True:
try:
str1 = input()
str2 = input()
m = len(str1)
n = len(str2)
dp = [[1 for i in range(n+1)] for j in range(m+1)]#重点注意二维数据的创建方法,重点注意其横竖坐标,注意注意
for i in range(n+1):
dp[0][i] = i
for j in range(m+1):
dp[j][0] = j
for i in range(1,m+1):
for j in range(1,n+1):
if str1[i-1] == str2[j-1]:#如果当前两个字母相同,则跳过,步数不增加
dp[i][j]=dp[i-1][j-1]
else: #如果两个字母不同,则有三种方式可以达成,删除、插入、替换,选择最小的前状态,步数加1
dp[i][j] = min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])+1
print(dp[m][n])
except:
break
HJ53 杨辉三角的变形

import sys
alt=[2,3,2,4] #发现规律,从第三行开始2324循环
for line in sys.stdin:
n=int(line.strip())
if n<3:
print牛客网真题练习-01
牛客网真题练习-01
双核处理
一种双核CPU的两个核能够同时的处理任务,现在有n个已知数据量的任务需要交给CPU处理,假设已知CPU的每个核1秒可以处理1kb,每个核同时只能处理一项任务。n个任务可以按照任意顺序放入CPU进行处理,现在需要设计一个方案让CPU处理完这批任务所需的时间最少,求这个最小的时间。
输入描述:
输入包括两行:
第一行为整数n(1 ≤ n ≤ 50)
第二行为n个整数length[i](1024 ≤ length[i] ≤ 4194304),表示每个任务的长度为length[i]kb,每个数均为1024的倍数。
输出描述:
输出一个整数,表示最少需要处理的时间
输入例子
5
3072 3072 7168 3072 1024
输出例子:
9216
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;
const int MAXN = 55;
const int MAXM = 800000;
int n,sum, num[MAXN], dp[MAXM];
int main(){
freopen("in.txt", "r", stdin);
int tmp, ans;
scanf("%d", &n);
sum = 0;
for(int i=0; i<n; ++i){
scanf("%d", &num[i]);
sum += num[i];
}
memset(dp, 0, sizeof(dp));
dp[0] = 1;
for(int i=0; i<n; ++i){
tmp = num[i]/1024;
for(int j=sum/1024; j>=tmp; --j){
if(dp[j - tmp] == 1){
dp[j] = 1;
}
}
}
ans = 0;
tmp = sum/(2*1024);
for(int i=0; i<sum/1024; ++i){
if(dp[tmp-i] == 1){
ans = 1024*(tmp-i);
break;
}
if(dp[tmp+i] == 1){
ans = 1024*(tmp+i);
break;
}
}
ans = max(sum-ans, ans);
printf("%d\n", ans );
return 0;
}
赶去公司
终于到周末啦!小易走在市区的街道上准备找朋友聚会,突然服务器发来警报,小易需要立即回公司修复这个紧急bug。假设市区是一个无限大的区域,每条街道假设坐标是(X,Y),小易当前在(0,0)街道,办公室在(gx,gy)街道上。小易周围有多个出租车打车点,小易赶去办公室有两种选择,一种就是走路去公司,另外一种就是走到一个出租车打车点,然后从打车点的位置坐出租车去公司。每次移动到相邻的街道(横向或者纵向)走路将会花费walkTime时间,打车将花费taxiTime时间。小易需要尽快赶到公司去,现在小易想知道他最快需要花费多少时间去公司。
输入描述:
输入数据包括五行:
第一行为周围出租车打车点的个数n(1 ≤ n ≤ 50)
第二行为每个出租车打车点的横坐标tX[i] (-10000 ≤ tX[i] ≤ 10000)
第三行为每个出租车打车点的纵坐标tY[i] (-10000 ≤ tY[i] ≤ 10000)
第四行为办公室坐标gx,gy(-10000 ≤ gx,gy ≤ 10000),以空格分隔
第五行为走路时间walkTime(1 ≤ walkTime ≤ 1000)和taxiTime(1 ≤ taxiTime ≤ 1000),以空格分隔
输出描述:
输出一个整数表示,小易最快能赶到办公室的时间
输入例子:
2
-2 -2
0 -2
-4 -2
15 3
输出例子:
42
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
using namespace std;
const int MAXN = 50;
int X[MAXN], Y[MAXN];
int main(){
freopen("in.txt", "r", stdin);
int ans, gx, gy, Wt, Tt, n, tmp;
scanf("%d", &n);
for(int i=0; i<n; ++i){
scanf("%d", &X[i]);
}
for(int i=0; i<n; ++i){
scanf("%d", &Y[i]);
}
scanf("%d%d", &gx, &gy);
scanf("%d%d", &Wt, &Tt);
ans = (abs(gx) + abs(gy))*Wt;
for(int i=0; i<n; ++i){
tmp = (abs(X[i]) + abs(Y[i]))*Wt + (abs(gx - X[i]) + abs(gy - Y[i]))*Tt;
if(tmp < ans){
ans = tmp;
}
}
printf("%d\n", ans );
return 0;
}
消除重复元素
小易有一个长度为n序列,小易想移除掉里面的重复元素,但是小易想是对于每种元素保留最后出现的那个。小易遇到了困难,希望你来帮助他。
输入描述:
输入包括两行:
第一行为序列长度n(1 ≤ n ≤ 50)
第二行为n个数sequence[i](1 ≤ sequence[i] ≤ 1000),以空格分隔
输出描述:
输出消除重复元素之后的序列,以空格分隔,行末无空格
输入例子:
9
100 100 100 99 99 99 100 100 100
输出例子:
99 100
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <map>
#include <vector>
using namespace std;
const int MAXN = 55;
int main(){
freopen("in.txt", "r", stdin);
int n, num[MAXN];
scanf("%d", &n);
for(int i=0; i<n; ++i){
scanf("%d", &num[i]);
}
vector<int> ans;
map<int, int> mp;
for(int i=n-1; i>=0; --i){
if( mp.find( num[i] ) == mp.end()){
mp[ num[i] ] = 1;
ans.push_back( num[i] );
}
}
for(int i=ans.size()-1;i>=0; --i){
if(i==0){
printf("%d\n", ans[i] );
}else{
printf("%d ", ans[i] );
}
}
return 0;
}
工作安排
现在有n位工程师和6项工作(编号为0至5),现在给出每个人能够胜任的工作序号表(用一个字符串表示,比如:045,表示某位工程师能够胜任0号,4号,5号工作)。现在需要进行工作安排,每位工程师只能被安排到自己能够胜任的工作当中去,两位工程师不能安排到同一项工作当中去。如果两种工作安排中有一个人被安排在的工作序号不一样就被视为不同的工作安排,现在需要计算出有多少种不同工作安排计划。
输入描述:
输入数据有n+1行:
第一行为工程师人数n(1 ≤ n ≤ 6)
接下来的n行,每行一个字符串表示第i(1 ≤ i ≤ n)个人能够胜任的工作(字符串不一定等长的)
输出描述:
输出一个整数,表示有多少种不同的工作安排方案
输入例子:
6
012345
012345
012345
012345
012345
012345
输出例子:
720
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
using namespace std;
const int MAXN = 10;
int n, ans, var[MAXN][MAXN], vis[MAXN];
void dfs(int cur){
if(cur == n){
ans++;
return;
}
for(int i=0; i<=5; ++i){
if(vis[i] == 0 && var[cur][i] == 1){
vis[i] = 1;
dfs(cur+1);
vis[i] = 0;
}
}
}
int main(){
freopen("in.txt", "r", stdin);
char st[MAXN];
scanf("%d", &n);
memset(var, 0, sizeof(var));
for(int i=0; i<n; ++i){
scanf("%s", st);
for(int j=0; j<strlen(st); ++j){
var[i][st[j]-‘0‘] = 1;
}
}
ans = 0;
memset(vis, 0, sizeof(vis));
dfs(0);
printf("%d\n", ans );
return 0;
}
奇怪的表达式求值
常规的表达式求值,我们都会根据计算的优先级来计算。比如*/的优先级就高于+-。但是小易所生活的世界的表达式规则很简单,从左往右依次计算即可,而且小易所在的世界没有除法,意味着表达式中没有/,只有(+, - 和 *)。现在给出一个表达式,需要你帮忙计算出小易所在的世界这个表达式的值为多少
输入描述:
输入为一行字符串,即一个表达式。其中运算符只有-,+,*。参与计算的数字只有0~9.
保证表达式都是合法的,排列规则如样例所示。
输出描述
输出一个数,即表达式的值
输入例子:
3+5*7
输出例子:
56
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;
const int MAXN = 100;
int main(){
char st[MAXN];
int flag, ans, tmp, len, i;
while(scanf("%s", st) != EOF){
ans = 0; len = strlen(st);
tmp = 0; i = 0; flag = 1;
while(i < len){
if(st[i] == ‘+‘){
flag = 1;
}else if(st[i] == ‘-‘){
flag = 2;
}else if(st[i] == ‘*‘){
flag = 3;
}else{
tmp = st[i] - ‘0‘;
while(i < len && st[i+1]>=‘0‘ && st[i+1]<=‘9‘){
i++;
tmp = tmp*10 + st[i]-‘0‘;
}
if(flag==1){
ans += tmp;
}else if(flag==2){
ans -= tmp;
}else{
ans *= tmp;
}
}
i++;
}
printf("%d", ans);
}
return 0;
}
涂棋盘
小易有一块n*n的棋盘,棋盘的每一个格子都为黑色或者白色,小易现在要用他喜欢的红色去涂画棋盘。小易会找出棋盘中某一列中拥有相同颜色的最大的区域去涂画,帮助小易算算他会涂画多少个棋格。
输入描述:
输入数据包括n+1行:
第一行为一个整数n(1 ≤ n ≤ 50),即棋盘的大小
接下来的n行每行一个字符串表示第i行棋盘的颜色,‘W‘表示白色,‘B‘表示黑色
输出描述:
输出小易会涂画的区域大小
输入例子:
3
BWW
BBB
BWB
输出例子:
3
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN = 55;
int n, ans, tmp, mp[MAXN][MAXN];
void dfs(int cx, int cy, int label){
tmp++;
mp[cx][cy] = 0;
if(cx+1<n && mp[cx+1][cy] == label){
dfs(cx+1, cy, label);
}
}
int main(){
char ch;
scanf("%d", &n);
for(int i=0; i<n; ++i){
getchar();
for(int j=0; j<n; ++j){
scanf("%c", &ch);
if(ch == ‘B‘){
mp[i][j] = -1;
}else{
mp[i][j] = 1;
}
}
}
ans = 0;
for(int i=0; i<n; ++i){
for(int j=0; j<n; ++j){
if(mp[i][j] != 0){
tmp = 0;
dfs(i, j, mp[i][j]);
if(tmp > ans){
ans = tmp;
}
}
}
}
printf("%d", ans);
return 0;
}
以上是关于「解析」牛客网-华为机考企业真题 41-60的主要内容,如果未能解决你的问题,请参考以下文章