pytorch深度学习模型调参策略：采用贝叶斯工具进行最优参数搜索及最佳步数确认

Posted 2023-03-29 颢师傅

目录

• 1.如何决定是否应用某个新的超参数配置
• 2.参数优化工具optuna确定最终最优配置
• • 为什么在调整的探索阶段使用准随机搜索而不是更复杂的黑盒优化算法？
  • optuna库简介
  • pytorch实现代码
  • 搜索参数详解
  • 输出结果
• 3.确定每次训练运行的步数
• • 使用学习率扫描选择max_train_steps初始候选值

1.如何决定是否应用某个新的超参数配置

简而言之，当我们决定对模型或训练过程进行更改或采用新的超参数配置时，我们需要考虑到结果中的不同变化来源。
对于试图改进模型的情况，我们可能会发现某个候选变化的验证误差最初比现有配置更好，但重复实验后并没有一致的优势。这些不一致的结果可能来自以下几个方面：

训练过程方差、重新训练方差或试验方差：使用相同的超参数但不同的随机种子进行训练运行之间的变化。

超参数搜索方差或研究方差：由于选择超参数的过程而导致结果的变化。

数据收集和抽样方差：从任何随机拆分到训练、验证和测试数据或由于训练数据生成过程而产生的方差。
为了决定是否采用候选变化，我们需要运行最佳试验N次，以了解试验之间的运行方差。我们应该只采用能够产生优势的变化，而不会增加任何复杂性。

2.参数优化工具optuna确定最终最优配置

我们完成对搜索空间的探索并确定需要调整的超参数后，贝叶斯优化工具是一个非常有吸引力的选择。此时，我们的重点将从学习有关调整问题的更多信息转变为生成一个最佳配置，以供启动或其他用途。因此，应该有一个经过精细调整的搜索空间，足够大，舒适地包含最佳观察试验周围的局部区域并已充分采样。我们的探索工作应该已经揭示了需要调整的最重要的超参数（以及它们的合理范围），可以使用它们来构建一个搜索空间，以尽可能大的调整预算进行最终自动调整研究。由于我们不再关心最大化对调整问题的洞察力，许多准随机搜索的优点不再适用，应该使用贝叶斯优化工具来自动找到最佳的超参数配置。开源的Vizier实现了各种复杂的算法来调整机器学习模型，包括贝叶斯优化算法。如果搜索空间包含大量发散点（损失值为NaN或比平均值高出许多标准差），则使用适当处理发散试验的黑盒优化工具非常重要。同时，我们还需要考虑在测试集上检查性能。原则上，我们甚至可以将验证集合并到训练集中，并使用贝叶斯优化找到的最佳配置进行重新训练。但是，仅当不会有特定工作负载的未来启动时才适用此方法（例如一次性的Kaggle竞赛）。

为什么在调整的探索阶段使用准随机搜索而不是更复杂的黑盒优化算法？

我们更喜欢基于低差异序列的准随机搜索，而不是更复杂的黑盒优化工具，因为它作为迭代调整过程的一部分，旨在最大化对调整问题的洞察力（我们称之为“探索阶段”）。贝叶斯优化和类似的工具更适合于开发阶段。
基于随机移位的低差异序列的准随机搜索可以看作是“抖动、洗牌的网格搜索”，因为它均匀但随机地探索给定的搜索空间，并且比随机搜索更广泛地扩展搜索点。
准随机搜索相对于更复杂的黑盒优化工具（如贝叶斯优化、进化算法）的优点包括：

非自适应采样搜索空间使得可能通过后续分析改变调整目标而不重新运行实验。

准随机搜索的一致性和统计可重复性。

准随机搜索对搜索空间的均匀探索使得更容易推理结果以及它们对搜索空间的建议。
运行不同数量的试验时，准随机搜索（或其他非自适应搜索算法）与自适应算法相比不会产生统计学上的不同结果。
更复杂的搜索算法可能不会始终正确处理不可行点，尤其是如果它们没有设计神经网络超参数调整。
准随机搜索简单易用，在许多调整试验将并行运行时表现尤为出色。
如果计算资源只允许并行运行少量试验，并且我们能够承担运行许多试验的序列，则尽管使调整结果更难以解释，贝叶斯优化变得更具吸引力。

optuna库简介

optuna是一个用于超参数优化的Python库。它提供了一种简单、高效的方法来搜索模型的最优超参数组合，以最大化或最小化目标函数（例如验证集准确率或损失函数）。optuna支持多种搜索算法，包括随机搜索、网格搜索和基于贝叶斯优化的搜索。它还支持并行化搜索，并提供了可视化工具来帮助用户分析搜索结果。使用optuna可以帮助用户节省大量时间和精力，从而更快地找到最优的超参数组合，并提高模型的性能。optuna不仅可以用于机器学习领域，也可以用于优化任何需要调整超参数的任务。

在默认情况下，Optuna 使用的是 TPE 算法进行贝叶斯优化搜索。该算法将搜索空间中的概率分布建模为两个条件概率分布：先验概率分布和似然概率分布。先验概率分布是指在未进行试验之前，对超参数的概率分布的假设。似然概率分布是指在已有的试验结果的基础上，对超参数的概率分布的推断。通过不断更新这两个概率分布，TPE 算法能够更快地收敛到全局最优解，并适应不同类型的搜索空间。
需要注意的是，虽然贝叶斯优化算法能够更快地收敛到全局最优解，但是其搜索效率与搜索空间的形状、维度、先验分布等因素都有关系。在使用 Optuna 进行超参数搜索时，我们应该根据具体的问题和实验情况，选择合适的搜索算法和搜索空间，以达到最优的搜索效果。
安装：

pip3 install optuna

pytorch实现代码

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision.datasets as datasets
import torchvision.transforms as transforms
import optuna
# 定义超参数搜索空间
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
def objective(trial):
    # 搜索学习率
    lr = trial.suggest_loguniform('lr', 1e-5, 1e-1)
    # 搜索动量因子
    momentum = trial.suggest_uniform('momentum', 0.0, 1.0)
    # 搜索权重衰减因子
    weight_decay = trial.suggest_loguniform('weight_decay', 1e-5, 1e-1)
    # 搜索网络结构超参数
    num_layers = trial.suggest_int('num_layers', 1, 5)
    hidden_size = trial.suggest_categorical('hidden_size', [32, 64, 128, 256])
    dropout = trial.suggest_uniform('dropout', 0.0, 0.5)
    # 加载CIFAR-10数据集
    transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
    train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
    test_dataset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
    train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=4)
    test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=128, shuffle=False, num_workers=4)
    # 定义模型
    model = nn.Sequential(
        nn.Flatten(),
        nn.Linear(32 * 32 * 3, hidden_size),
        nn.ReLU(),
        nn.Dropout(dropout),
        *(nn.Sequential(nn.Linear(hidden_size, hidden_size), nn.ReLU(), nn.Dropout(dropout)) for _ in range(num_layers - 1)),
        nn.Linear(hidden_size, 10),
    )
    if torch.cuda.device_count() > 1:
        #如果gpu设备数目大于1个，同时使用两个GPU
        model = nn.DataParallel(model, [0, 1])
    model=model.to(device)
    # 定义损失函数和优化器
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.SGD(model.parameters(), lr=lr, momentum=momentum, weight_decay=weight_decay)
    # 训练模型
    max_accuracy = float('-inf')
    accuracy_list = []
    for epoch in range(10):
        for i, (inputs, labels) in enumerate(train_loader):
            optimizer.zero_grad()
            inputs, labels = inputs.to(device), labels.to(device)
            outputs = model(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
        # 在测试集上测试模型性能
        correct = 0
        total = 0
        with torch.no_grad():
            for inputs, labels in test_loader:
                inputs, labels = inputs.to(device), labels.to(device)
                outputs = model(inputs)
                _, predicted = torch.max(outputs, dim=1)
                total += labels.size(0)
                correct += (predicted == labels).sum().item()
        accuracy = correct / total
        trial.report(accuracy, epoch)
        max_accuracy = max(max_accuracy, accuracy)
        accuracy_list.append(accuracy)
        if len(accuracy_list) > 5:
            accuracy_list.pop(0)
        max_accuracy_over_last_5_epochs = max(accuracy_list)
        # 提前停止条件：如果最近5个epoch的性能较最优值都没有提高，则停止训练
        if max_accuracy > max_accuracy_over_last_5_epochs:
           break
    return accuracy
if __name__ == '__main__':
    study = optuna.create_study(direction='maximize')
    study.optimize(objective, n_trials=100)
    print('Best trial:')
    trial = study.best_trial
    print('  Value: '.format(trial.value))
    print('  Params: ')
    for key, value in trial.params.items():
        print('    : '.format(key, value))

上述代码使用了 Optuna 提供的 suggest 方法来搜索超参数。具体来说，suggest_loguniform 方法用于搜索一个对数均匀分布中的数值，suggest_uniform 方法用于搜索一个均匀分布中的数值，suggest_int 方法用于搜索一个整数范围中的数值，suggest_categorical 方法用于搜索一组离散的数值。下面分别解释这些方法的用法：

搜索参数详解

trial.suggest_loguniform(‘lr’, 1e-5, 1e-1)：搜索一个对数均匀分布中的数值，用于学习率超参数 lr。对数均匀分布是指在对数尺度上均匀分布的分布，它通常用于搜索连续的正数超参数。这里我们搜索的范围是 [1e-5, 1e-1]。

trial.suggest_uniform(‘momentum’, 0.0, 1.0)：搜索一个均匀分布中的数值，用于动量因子超参数 momentum。均匀分布是指在给定的范围内均匀分布的分布，它通常用于搜索连续的超参数。这里我们搜索的范围是 [0.0, 1.0]。

trial.suggest_loguniform(‘weight_decay’, 1e-5, 1e-1)：搜索一个对数均匀分布中的数值，用于权重衰减因子超参数 weight_decay。这里我们搜索的范围是 [1e-5, 1e-1]。

trial.suggest_int(‘num_layers’, 1, 5)：搜索一个整数范围中的数值，用于网络层数超参数 num_layers。这里我们搜索的范围是 [1, 5]。

trial.suggest_categorical(‘hidden_size’, [32, 64, 128, 256])：搜索一组离散的数值，用于隐藏层神经元个数超参数 hidden_size。这里我们搜索的数值是 [32, 64, 128, 256] 中的一个。

trial.suggest_uniform(‘dropout’, 0.0, 0.5)：搜索一个均匀分布中的数值，用于 dropout 超参数 dropout。这里我们搜索的范围是 [0.0, 0.5]。

在每次试验中，Optuna 会根据超参数搜索空间中的分布，为每个超参数生成一个候选值，供模型训练使用。模型训练过程中，我们使用这些超参数的候选值来训练模型，并将模型在验证集上的表现作为试验的结果报告给 Optuna。Optuna 根据这些结果，不断更新超参数搜索空间中的概率分布，以提高搜索效率，并逐步找到最优的超参数组合。

输出结果

最终输出：

[I 2023-03-28 08:27:02,336] Trial 99 finished with value: 0.5207 and parameters: 'lr': 0.0413617890693661, 'momentum': 0.6396519061675595, 'weight_decay': 3.840413828120234e-05, 'num_layers': 1, 'hidden_size': 256, 'dropout': 0.023284222799990092. Best is trial 66 with value: 0.5493.
Best trial:
  Value: 0.5493
  Params: 
    lr: 0.07048135305238855
    momentum: 0.45078184234468277
    weight_decay: 6.0485982461392196e-05
    num_layers: 2
    hidden_size: 256
    dropout: 0.017699021560325236

3.确定每次训练运行的步数

工作负载可以分为两种：计算受限和非计算受限的。当训练是计算受限的时候，训练受到的限制是我们愿意等待的时间，而不是我们有多少训练数据或其他因素。
在这种情况下，如果我们能够以某种方式更长时间或更有效地训练，我们应该会看到更低的训练损失，并且通过适当的调整，可以改善验证损失。换句话说，加快训练等同于改善训练，而“最佳”训练时间始终是“尽可能长”。
尽管如此，只因为工作负载受计算限制，并不意味着训练更长/更快是改善结果的唯一方法。
当训练不受计算限制时，我们可以承受尽可能长时间的训练，但在某些时候，训练时间更长并没有太大的帮助（甚至会导致问题的过拟合）。
在这种情况下，我们应该期望能够训练到非常低的训练损失，直到训练时间更长可能会略微降低训练损失，但不会实质性地降低验证损失。特别是当训练不受计算限制时，更慷慨的训练时间预算可以使调整更容易，特别是在调整学习率衰减计划时，因为它们与训练预算有着特别强的相互作用。
换句话说，非常吝啬的训练时间预算可能需要调整到完美的学习率衰减计划，以实现良好的错误率。
无论给定的工作负载是否受计算限制，增加梯度的方差（跨批次）的方法通常会导致训练进度变慢，因此可能会增加达到特定验证损失所需的训练步数。高梯度方差可能是由以下原因引起：

（1）使用较小的批量大小
（2）添加数据增强
（3）添加某些类型的正则化（例如dropout）

使用学习率扫描选择max_train_steps初始候选值

该算法假定可以使用恒定的学习率计划不仅“完美地”拟合训练集，还可以找到一个最优的max_train_steps值。首先，找到任何最优配置（具有某个max_train_steps值）并将其用作起点。然后，在不使用数据增强和正则化的情况下，运行恒定的学习率扫描，在N步训练每个试验的情况下网格搜索学习率。扫描中最快试验达到完全训练性能所需的步骤数是max_train_steps的初始猜测。但需要注意的是，不良的搜索空间可能会导致自我欺骗。因此，至少应检查最优搜索空间是否足够宽广。

使用贝叶斯优化工具实践XGBoost回归模型调参

0. 关于调参

0.1. 超参数

在机器学习的上下文中，超参数（hyper parameters）是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果。

例如深度学习中的学习率、批次大小（batch_size）、优化器（optimizer）等，XGBoost算法中的最大的树深度（max_depth）、子样本比例（subsample）、子节点最小权重和（min_child_weight）等。

0.2. 调参方法

超参数设置通常调参方法如下：

• 随机搜索 （RandomSearch），搜索超参数的值不是固定，是在一定范围内随机的值；
• 网格搜索（GridSearch ），给定超参和取值范围，遍历所有组合得到最优参数。首先你要给定一个先验的取值，不能取得太多，否则组合太多，耗时太长，可以启发式的尝试；
• 贝叶斯优化（Bayesian optimization），采用高斯过程迭代式的寻找最优参数，每次迭代都是在上一次迭代基础上拟合高斯函数上，寻找比上一次迭代更优的参数。

本文主要是分享贝叶斯优化调参方法，其他略。

1. 贝叶斯优化理论

贝叶斯优化是一种逼近思想，当计算非常复杂、迭代次数较高时能起到很好的效果，多用于超参数确定。

贝叶斯优化算法主要包含两个核心部分——概率代理模型（probabilistic surrogate model）和采集函数
(acquisition function)。

• 概率代理模型包含先验概率模型和观测模型：先验概率模$p(f)$；观测模型描述观测数据生成的机
  制，即似然分布$p(D|f)$。更新概率代理模型意味着根据公式 (1)得到包含更多数据信息的后验概率分布
  $p(f|D_i)$。
• 采集函数是根据后验概率分布（高斯过程）构造的，通过最大化采集函数来选择下一个最有 “潜 力”的评估点。同时 ，有效的采集函数能够保证选择的评估点序列使得总损失(loss)最小．损失有 时表示为regret：
  $$r_n=|y^{\ast }-y_n|$$
  或者累计表示为：$$R_i=\sum _{i=1}^n$$其中，$y^{\ast }$表示当前最优解。

掌握贝叶斯优化调参，须要从三个部分讲起：

• 贝叶斯定理
• 高斯过程，用以拟合优化目标函数
• 贝叶斯优化，包括了“开采”和“勘探”，用以花最少的代价找到最优值

1.1. 贝叶斯定理

贝叶斯优化名称的由来是因为参数优化中使用了贝叶斯定理。

$$p(f|D_i)=\frac{p(D_i|f)p(f)}{p(D_i)}(1)$$

其中，$f$表示未知目标函数（或者标识参数模型中的参数）：

• $D_i=(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$表示已观测集合，$x_i$表示决策向量，$y_i=f(x_i)+{\epsilon }_i$表示观测值误差；
• $p(D_i|f)$表示$y$的似然分布；
• $p(f)$表示$f$先验概率分布，对未知目标函数的假设；
• $p(D_i)$表示边际化$f$的边际似然分布或者“证据”，由于该边际似然存在概率密度函数的乘积和积 分，通 常难以得到明确的解析式，该边际似然在贝叶斯优化中主要用于优化超参数(hyper-parameter)；
• $p(f|D_i)$表示$f$的后验概率分布，后验概率分布描述通过己观测数据集对先验进行修正后未知目标函数的置信度。

贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。

1.2. 高斯过程（Gaussian Process）

高斯过程（GP）全称是高斯分布随机过程，是一个可以被用来表示函数的分布情况的模型。当前，机器学习的常见做法是把函数参数化，然后用产生的参数建模来规避分布表示（如线性回归的权重）。但GP不同，它直接对函数建模生成非参数模型。由此产生的一个突出优势就是它不仅能模拟任何黑盒函数，还能模拟不确定性。这种对不确定性的量化是十分重要的，如当我们被允许请求更多数据时，依靠高斯过程，我们能探索最不可能实现高效训练的数据区域。这也是贝叶斯优化背后的主要思想。

那么高斯分布是如何计算的呢？

假设$f\sim GP(\mu ,K)$，对于$GP$高斯过程，其中$\mu$为均值，$K$为协方差核。所以预测也是服从正态分布的，即有$p(y|x,D)=N(\hat{y},{\hat{\sigma }}^2)$。

当随机变量的维度上升到有限$n$的时候，称之为高维高斯分布，$p(x)=N(\mu ,{\sum }_{n\times n})$。

对于一个$n$维的高斯分布而言，决定它的分布是两个参数：

• $n$维均值向量${\mu }_n$，表示$n$维高斯分布中各个维度随机变量的期望；
• $n\times n$的协方差矩阵${\sum }_{n\times n}$，表示高维分布中，各个维度自身的方差，以及不同维度间的协方差。

核函数(协方差函数)

核函数是一个高斯过程的核心，核函数决定了一个高斯过程的性质。核函数在高斯过程中起生成一个协方差矩阵(相关系数矩阵)来衡量任意两个点之间的“距离”。不同的核函数有不同的衡量方法，得到的高斯过程的性质也不一样。最常用的一个核函数为高斯核函数，也成为径向基函数 RBF。其基本形式如下。

$$K(x_i,x_j)={\sigma }^{2}exp(-\frac{||x_i-x_j|{|}_2^2}{2l^2})$$

其中$\sigma$和$l$是高斯核的超参数。

本文使用的BayesianOptimization的源代码中，高斯过程使用了sklearn.gaussian_process，如下截部分取代码所示。

from sklearn.gaussian_process.kernels import Matern
from sklearn.gaussian_process import GaussianProcessRegressor
......
        self._random_state = ensure_rng(random_state)

        # Data structure containing the function to be optimized, the bounds of
        # its domain, and a record of the evaluations we have done so far
        self._space = TargetSpace(f, pbounds, random_state)

        # queue
        self._queue = Queue()

        # Internal GP regressor
        self._gp = GaussianProcessRegressor(
            kernel=Matern(nu=2.5),
            alpha=1e-6,
            normalize_y=True,
            n_restarts_optimizer=5,
            random_state=self._random_state,
        )

        self._verbose = verbose
        self._bounds_transformer = bounds_transformer
        if self._bounds_transformer:
            self._bounds_transformer.initialize(self._space)

        super(BayesianOptimization, self).__init__(events=DEFAULT_EVENTS)

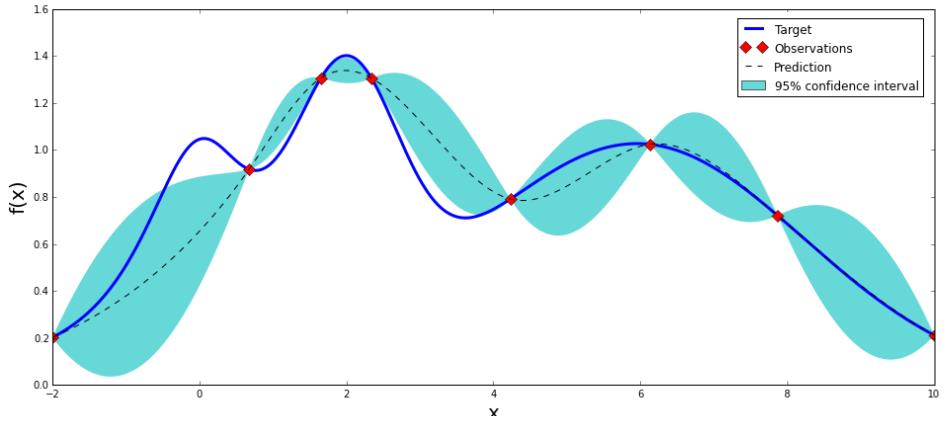
上图是一张高斯分布拟合函数的示意图，可以看到，它只需要九个点，就可以大致拟合出整个函数形状（图片来自：https://github.com/fmfn/BayesianOptimization）

1.3. 贝叶斯优化

参数优化基本思想是基于数据使用贝叶斯定理估计目标函数的后验分布，然后再根据分布选择下一个采样的超参数组合。它充分利用了前一个采样点的信息，其优化的工作方式是通过对目标函数形状的学习，并找到使结果向全局最大提升的参数。

假设一组超参数组合是 X = x 1 , x 2 , . . . x n X=x_1,x_2,...x_n X=x1​,x使用贝叶斯优化工具实践XGBoost回归模型调参

随机森林算法及贝叶斯优化调参Python实践

随机森林算法及贝叶斯优化调参Python实践

随机森林算法及贝叶斯优化调参Python实践

强大而精致的机器学习调参方法：贝叶斯优化

数据挖掘机器学习[四]---汽车交易价格预测详细版本｛嵌入式特征选择（XGBoots,LightGBM），模型调参（贪心网格贝叶斯调参）｝