深度强化学习 DDPG 模型解析，附Pytorch完整代码

Posted 2023-03-29 立Sir

大家好，今天和各位分享一下深度确定性策略梯度算法 (Deterministic Policy Gradient，DDPG)。并基于 OpenAI 的 gym 环境完成一个小游戏。完整代码在我的 GitHub 中获得：

https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Model

---

1. 基本原理

深度确定性策略梯度算法是结合确定性策略梯度算法的思想，对 DQN 的一种改进，是一种无模型的深度强化学习算法。

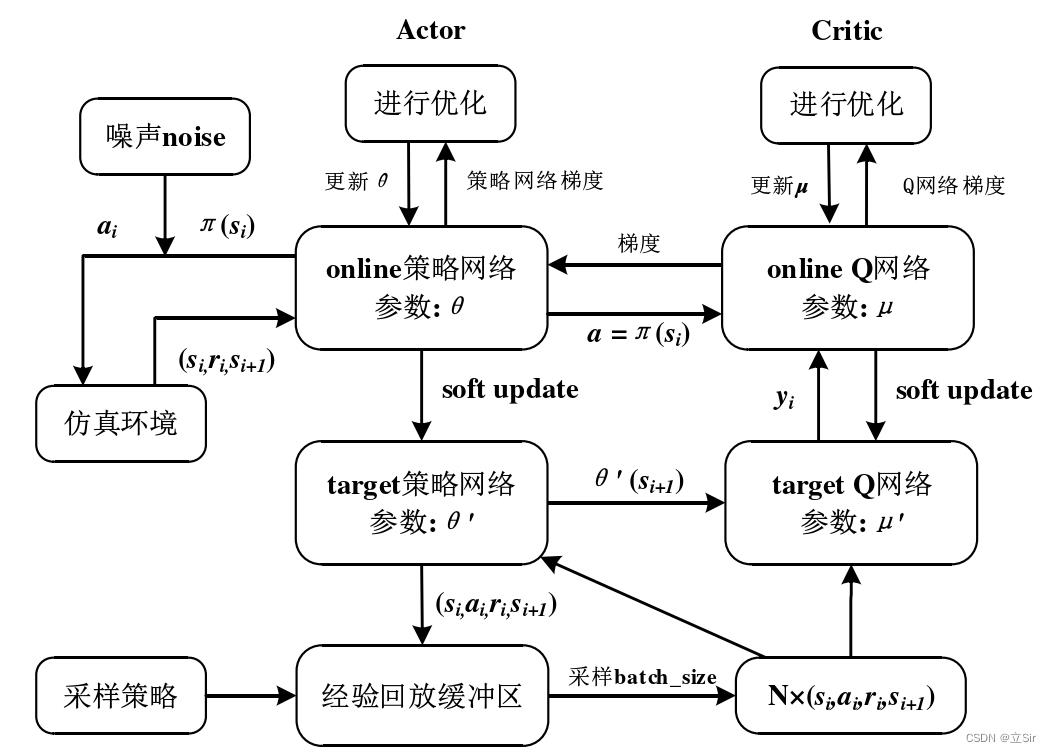
DDPG 算法使用演员-评论家（Actor-Critic）算法作为其基本框架，采用深度神经网络作为策略网络和动作值函数的近似，使用随机梯度法训练策略网络和价值网络模型中的参数。DDPG 算法的原理如下图所示。

DDPG 算法架构中使用双重神经网络架构，对于策略函数和价值函数均使用双重神经网络模型架构（即 Online 网络和 Target 网络），使得算法的学习过程更加稳定，收敛的速度加快。同时该算法引入经验回放机制，Actor 与环境交互生产生的经验数据样本存储到经验池中，抽取批量数据样本进行训练，即类似于 DQN 的经验回放机制，去除样本的相关性和依赖性，使得算法更加容易收敛。 

---

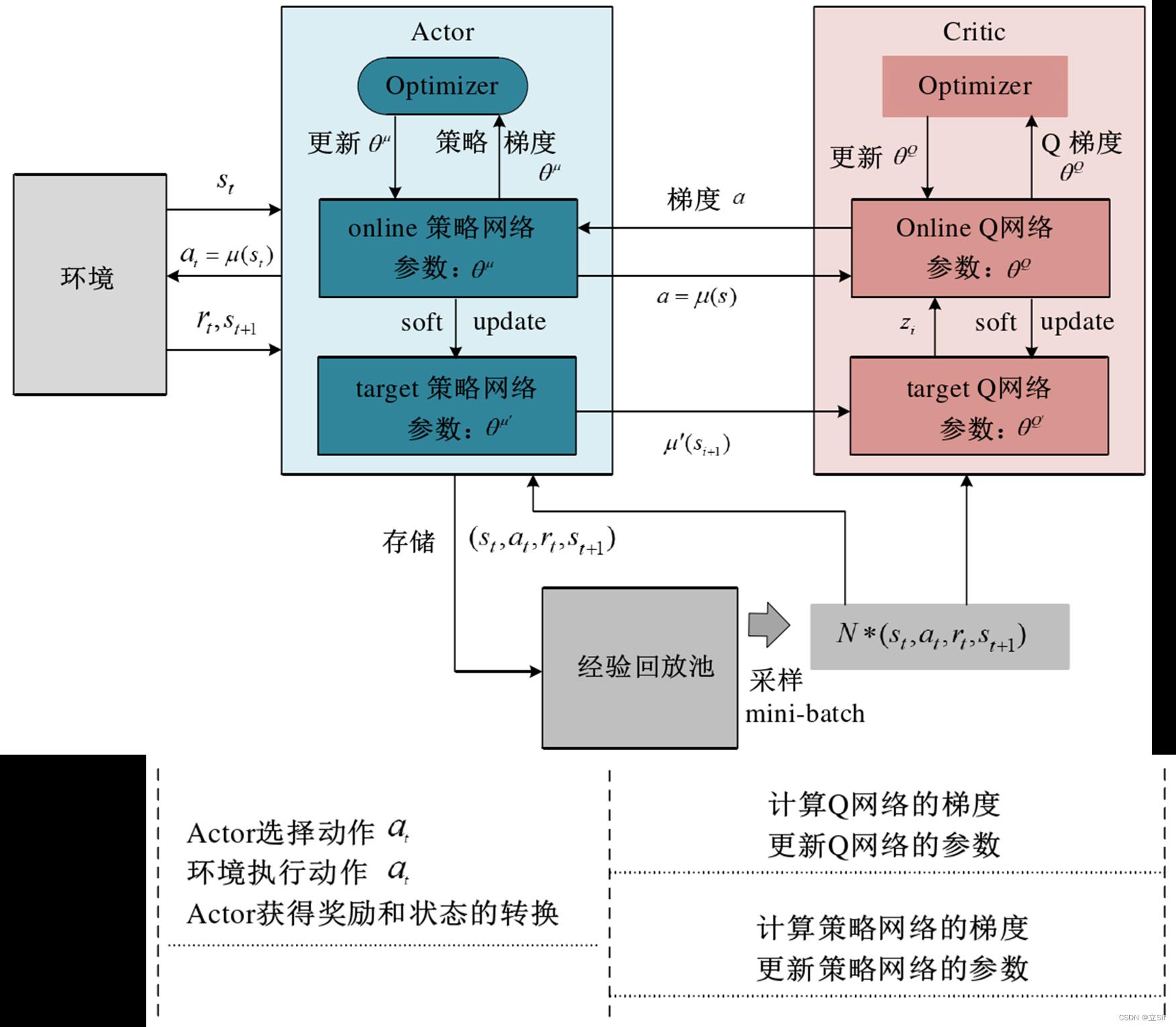
2. 公式推导

为了便于大家理解 DDPG 的推导过程，算法框架如下图所示：

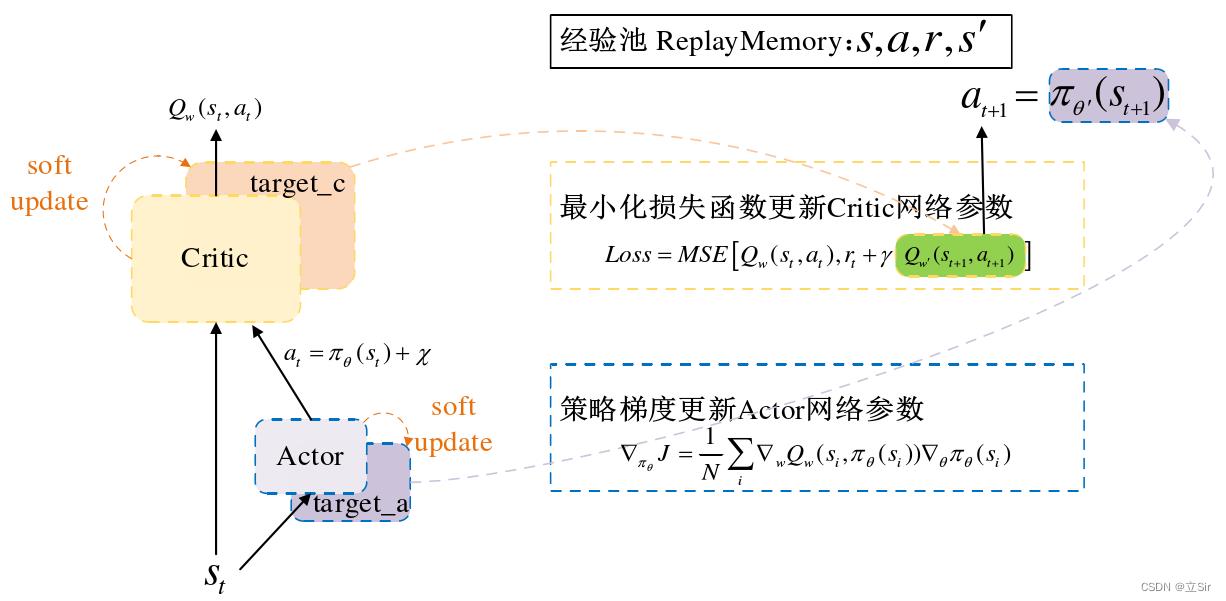
DDPG 共包含 4 个神经网络，用于对 Q 值函数和策略的近似表示。Critic 目标网络用于近似估计下一时刻的状态-动作的 Q 值函数 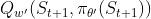，其中，下一动作值是通过 Actor 目标网络近似估计得到的 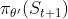。于是可以得到当前状态下 Q 值函数的目标值：

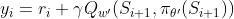
Critic 训练网络输出当前时刻状态-动作的 Q 值函数 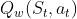，用于对当前策略评价。为了增加智能体在环境中的探索，DDPG 在行为策略上添加了高斯噪声函数。Critic 网络的目标定义为：

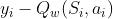
通过最小化损失值（均方误差损失）来更新 Critic 网络的参数，Critic 网络更新时的损失函数为：

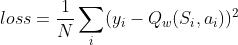
其中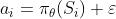，， 代表行为策略上的探索噪声。

Actor 目标网络用于提供下一个状态的策略，Actor 训练网络则是提供当前状态的策略，结合 Critic 训练网络的 Q 值函数可以得到 Actor 在参数更新时的策略梯度：

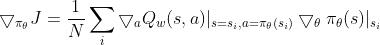
对于目标网络参数 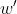 和 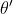 的更新，DDPG 通过软更新机制（每次 learn 的时候更新部分参数）保证参数可以缓慢更新，从而提高学习的稳定性：

DDPG 中既有基于价值函数的方法特征，也有基于策略的方法特征，使深度强化学习可以处理连续动作，并且具有一定的探索能力。 

算法流程图如下：

---

3. 代码实现

DDPG 的伪代码如下：

模型代码如下：

import torch
from torch import nn
from torch.nn import functional as F
import numpy as np
import collections
import random

# ------------------------------------- #
# 经验回放池
# ------------------------------------- #

class ReplayBuffer:
    def __init__(self, capacity):  # 经验池的最大容量
        # 创建一个队列，先进先出
        self.buffer = collections.deque(maxlen=capacity)
    # 在队列中添加数据
    def add(self, state, action, reward, next_state, done):
        # 以list类型保存
        self.buffer.append((state, action, reward, next_state, done))
    # 在队列中随机取样batch_size组数据
    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)
        # 将数据集拆分开来
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done
    # 测量当前时刻的队列长度
    def size(self):
        return len(self.buffer)

# ------------------------------------- #
# 策略网络
# ------------------------------------- #

class PolicyNet(nn.Module):
    def __init__(self, n_states, n_hiddens, n_actions, action_bound):
        super(PolicyNet, self).__init__()
        # 环境可以接受的动作最大值
        self.action_bound = action_bound
        # 只包含一个隐含层
        self.fc1 = nn.Linear(n_states, n_hiddens)
        self.fc2 = nn.Linear(n_hiddens, n_actions)
    # 前向传播
    def forward(self, x):
        x = self.fc1(x)  # [b,n_states]-->[b,n_hiddens]
        x = F.relu(x)
        x = self.fc2(x)  # [b,n_hiddens]-->[b,n_actions]
        x= torch.tanh(x)  # 将数值调整到 [-1,1]
        x = x * self.action_bound  # 缩放到 [-action_bound, action_bound]
        return x

# ------------------------------------- #
# 价值网络
# ------------------------------------- #

class QValueNet(nn.Module):
    def __init__(self, n_states, n_hiddens, n_actions):
        super(QValueNet, self).__init__()
        # 
        self.fc1 = nn.Linear(n_states + n_actions, n_hiddens)
        self.fc2 = nn.Linear(n_hiddens, n_hiddens)
        self.fc3 = nn.Linear(n_hiddens, 1)
    # 前向传播
    def forward(self, x, a):
        # 拼接状态和动作
        cat = torch.cat([x, a], dim=1)  # [b, n_states + n_actions]
        x = self.fc1(cat)  # -->[b, n_hiddens]
        x = F.relu(x)
        x = self.fc2(x)  # -->[b, n_hiddens]
        x = F.relu(x)
        x = self.fc3(x)  # -->[b, 1]
        return x

# ------------------------------------- #
# 算法主体
# ------------------------------------- #

class DDPG:
    def __init__(self, n_states, n_hiddens, n_actions, action_bound,
                 sigma, actor_lr, critic_lr, tau, gamma, device):

        # 策略网络--训练
        self.actor = PolicyNet(n_states, n_hiddens, n_actions, action_bound).to(device)
        # 价值网络--训练
        self.critic = QValueNet(n_states, n_hiddens, n_actions).to(device)
        # 策略网络--目标
        self.target_actor = PolicyNet(n_states, n_hiddens, n_actions, action_bound).to(device)
        # 价值网络--目标
        self.target_critic = QValueNet(n_states, n_hiddens, n_actions).to(device
                                                                          )
        # 初始化价值网络的参数，两个价值网络的参数相同
        self.target_critic.load_state_dict(self.critic.state_dict())
        # 初始化策略网络的参数，两个策略网络的参数相同
        self.target_actor.load_state_dict(self.actor.state_dict())

        # 策略网络的优化器
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        # 价值网络的优化器
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)

        # 属性分配
        self.gamma = gamma  # 折扣因子
        self.sigma = sigma  # 高斯噪声的标准差，均值设为0
        self.tau = tau  # 目标网络的软更新参数
        self.n_actions = n_actions
        self.device = device

    # 动作选择
    def take_action(self, state):
        # 维度变换 list[n_states]-->tensor[1,n_states]-->gpu
        state = torch.tensor(state, dtype=torch.float).view(1,-1).to(self.device)
        # 策略网络计算出当前状态下的动作价值 [1,n_states]-->[1,1]-->int
        action = self.actor(state).item()
        # 给动作添加噪声，增加搜索
        action = action + self.sigma * np.random.randn(self.n_actions)
        return action
    
    # 软更新, 意思是每次learn的时候更新部分参数
    def soft_update(self, net, target_net):
        # 获取训练网络和目标网络需要更新的参数
        for param_target, param in zip(target_net.parameters(), net.parameters()):
            # 训练网络的参数更新要综合考虑目标网络和训练网络
            param_target.data.copy_(param_target.data*(1-self.tau) + param.data*self.tau)

    # 训练
    def update(self, transition_dict):
        # 从训练集中取出数据
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)  # [b,n_states]
        actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1,1).to(self.device)  # [b,1]
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)  # [b,1]
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)  # [b,next_states]
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)  # [b,1]
        
        # 价值目标网络获取下一时刻的动作[b,n_states]-->[b,n_actors]
        next_q_values = self.target_actor(next_states)
        # 策略目标网络获取下一时刻状态选出的动作价值 [b,n_states+n_actions]-->[b,1]
        next_q_values = self.target_critic(next_states, next_q_values)
        # 当前时刻的动作价值的目标值 [b,1]
        q_targets = rewards + self.gamma * next_q_values * (1-dones)
        
        # 当前时刻动作价值的预测值 [b,n_states+n_actions]-->[b,1]
        q_values = self.critic(states, actions)

        # 预测值和目标值之间的均方差损失
        critic_loss = torch.mean(F.mse_loss(q_values, q_targets))
        # 价值网络梯度
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        # 当前状态的每个动作的价值 [b, n_actions]
        actor_q_values = self.actor(states)
        # 当前状态选出的动作价值 [b,1]
        score = self.critic(states, actor_q_values)
        # 计算损失
        actor_loss = -torch.mean(score)
        # 策略网络梯度
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # 软更新策略网络的参数  
        self.soft_update(self.actor, self.target_actor)
        # 软更新价值网络的参数
        self.soft_update(self.critic, self.target_critic)

---

4. 案例演示

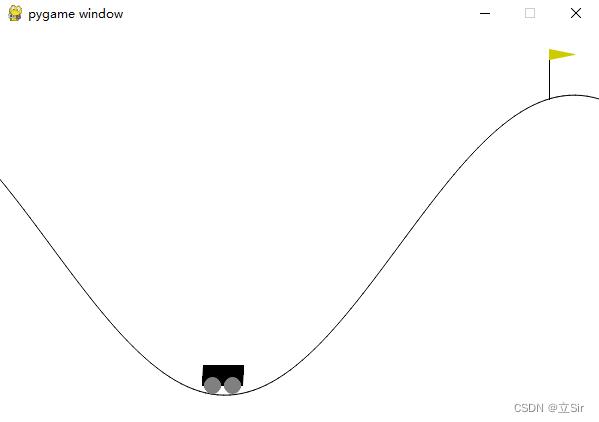
基于 OpenAI 的 gym 环境完成一个推车游戏，目标是将小车推到山顶旗子处。动作维度为1，属于连续值；状态维度为 2，分别是 x 坐标和小车速度。

代码如下：

import numpy as np
import torch
import matplotlib.pyplot as plt
import gym
from parsers import args
from RL_brain import ReplayBuffer, DDPG
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')

# -------------------------------------- #
# 环境加载
# -------------------------------------- #

env_name = "MountainCarContinuous-v0"  # 连续型动作
env = gym.make(env_name, render_mode="human")
n_states = env.observation_space.shape[0]  # 状态数 2
n_actions = env.action_space.shape[0]  # 动作数 1
action_bound = env.action_space.high[0]  # 动作的最大值 1.0


# -------------------------------------- #
# 模型构建
# -------------------------------------- #

# 经验回放池实例化
replay_buffer = ReplayBuffer(capacity=args.buffer_size)
# 模型实例化
agent = DDPG(n_states = n_states,  # 状态数
             n_hiddens = args.n_hiddens,  # 隐含层数
             n_actions = n_actions,  # 动作数
             action_bound = action_bound,  # 动作最大值
             sigma = args.sigma,  # 高斯噪声
             actor_lr = args.actor_lr,  # 策略网络学习率
             critic_lr = args.critic_lr,  # 价值网络学习率
             tau = args.tau,  # 软更新系数
             gamma = args.gamma,  # 折扣因子
             device = device
            )

# -------------------------------------- #
# 模型训练
# -------------------------------------- #

return_list = []  # 记录每个回合的return
mean_return_list = []  # 记录每个回合的return均值

for i in range(10):  # 迭代10回合
    episode_return = 0  # 累计每条链上的reward
    state = env.reset()[0]  # 初始时的状态
    done = False  # 回合结束标记

    while not done:
        # 获取当前状态对应的动作
        action = agent.take_action(state)
        # 环境更新
        next_state, reward, done, _, _ = env.step(action)
        # 更新经验回放池
        replay_buffer.add(state, action, reward, next_state, done)
        # 状态更新
        state = next_state
        # 累计每一步的reward
        episode_return += reward

        # 如果经验池超过容量，开始训练
        if replay_buffer.size() > args.min_size:
            # 经验池随机采样batch_size组
            s, a, r, ns, d = replay_buffer.sample(args.batch_size)
            # 构造数据集
            transition_dict = 
                'states': s,
                'actions': a,
                'rewards': r,
                'next_states': ns,
                'dones': d,
            
            # 模型训练
            agent.update(transition_dict)
    
    # 保存每一个回合的回报
    return_list.append(episode_return)
    mean_return_list.append(np.mean(return_list[-10:]))  # 平滑

    # 打印回合信息
    print(f'iter:i, return:episode_return, mean_return:np.mean(return_list[-10:])')

# 关闭动画窗格
env.close()

# -------------------------------------- #
# 绘图
# -------------------------------------- #

x_range = list(range(len(return_list)))

plt.subplot(121)
plt.plot(x_range, return_list)  # 每个回合return
plt.xlabel('episode')
plt.ylabel('return')
plt.subplot(122)
plt.plot(x_range, mean_return_list)  # 每回合return均值
plt.xlabel('episode')
plt.ylabel('mean_return')

深度强化学习 DQN 模型解析，附Pytorch完整代码

大家好，今天和各位讲解一下深度强化学习中的基础模型 DQN，配合 OpenAI 的 gym 环境，训练模型完成一个小游戏，完整代码可以从我的 GitHub 中获得：

https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Model

---

1. 算法原理

1.1 基本原理

DQN（Deep Q Network）算法由 DeepMind 团队提出，是深度神经网络和 Q-Learning 算法相结合的一种基于价值的深度强化学习算法。

Q-Learning 算法构建了一个状态-动作值的 Q 表，其维度为 (s,a)，其中 s 是状态的数量，a 是动作的数量，根本上是 Q 表将状态和动作映射到 Q 值。此算法适用于状态数量能够计算的场景。但是在实际场景中，状态的数量可能很大，这使得构建 Q 表难以解决。为破除这一限制，我们使用 Q 函数来代替 Q 表的作用，后者将状态和动作映射到 Q 值的结果相同。

由于神经网络擅长对复杂函数进行建模，因此我们用其当作函数近似器来估计此 Q 函数，这就是 Deep Q Networks。此网络将状态映射到可从该状态执行的所有动作的 Q 值。即只要输入一个状态，网络就会输出当前可执行的所有动作分别对应的 Q 值。如下图所示，它学习网络的权重，以此输出最佳 Q 值。

---

1.2 模型结构

DQN 体系结构主要包含：Q 网络、目标网络，以及经验回放组件。.Q 网络是经过训练以生成最佳状态-动作值的 agent。经验回放单元的作用是与环境交互，生成数据以训练 Q 网络。目标网络与 Q 网络在初始时是完全相同的。DQN 工作流程图如下

---

1.2.1  经验回放

经验回放从当前状态中以贪婪策略  选择一个动作，执行后从环境中获得奖励和下一步的状态，如下图所示。

然后将此观测值另存为用于训练数据的样本，如下图所示。

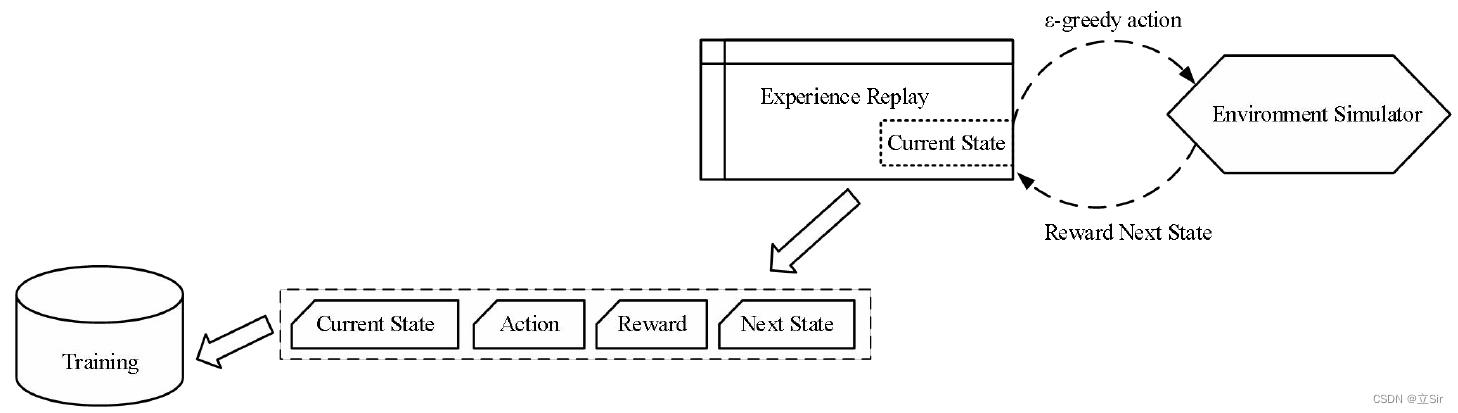
与 Q Learning 算法不同，经验回放组件的存在有其必须性。神经网络通常接受一批数据，如果我们用单个样本去训练它，每个样本和相应的梯度将具有很大的方差，并且会导致网络权重永远不会收敛。

当我们训练神经网络时，最好的做法是在随机打乱的训练数据中选择一批样本。这确保了训练数据有足够的多样性，使网络能够学习有意义的权重，这些权重可以很好地泛化并且可以处理一系列数据值。如果我们以顺序动作传递一批数据，则不会达到此效果。

所以可得出结论：顺序操作彼此高度相关，并且不会像网络所希望的那样随机洗牌。这导致了一个 “灾难性遗忘” 的问题，网络忘记了它不久前学到的东西。

以上是引入经验回放组件的原因。智能体在内存容量范围内从一开始就执行的所有动作和观察都将被存储。然后从此存储器中随机选择一批样本。这确保了批次是经过打乱，并且包含来自旧样品和较新样品的足够多样性，这样能保证训练过的网络具有能处理所有场景的权重。

# --------------------------------------- #
# 经验回放池
# --------------------------------------- #

class ReplayBuffer():
    def __init__(self, capacity):
        # 创建一个先进先出的队列，最大长度为capacity，保证经验池的样本量不变
        self.buffer = collections.deque(maxlen=capacity)
    # 将数据以元组形式添加进经验池
    def add(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))
    # 随机采样batch_size行数据
    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)  # list, len=32
        # *transitions代表取出列表中的值，即32项
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done
    # 目前队列长度
    def size(self):
        return len(self.buffer)

---

1.2.2 Q 网络预测 Q 值

所有之前的经验回放都将保存为训练数据。现在从此训练数据中随机抽取一批样本，以便它包含较旧样本和较新样本的混合。随后将这批训练数据输入到两个网络。Q 网络从每个数据样本中获取当前状态和操作，并预测该特定操作的 Q 值，这是“预测 Q 值”。如下图所示。

---

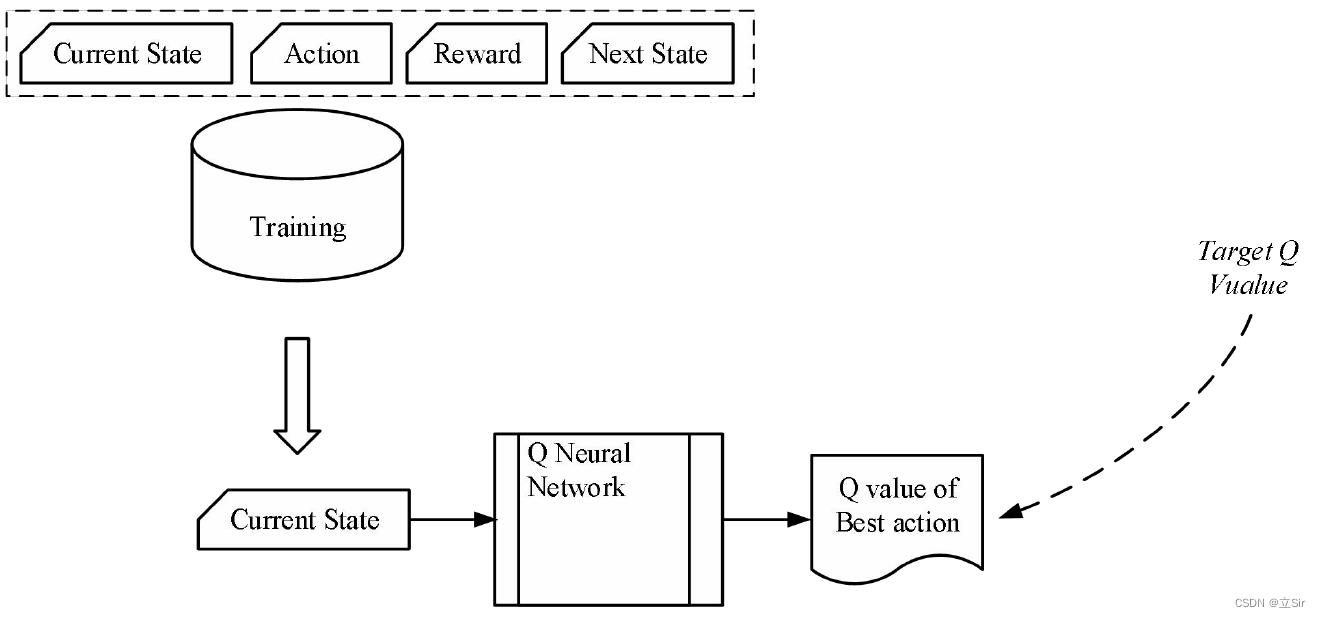
1.2.3 目标网络预测目标 Q 值

目标网络从每个数据样本中获取下一个状态，并可以从该状态执行的所有操作中预测最佳 Q 值，这是“目标 Q 值”。如下图所示。

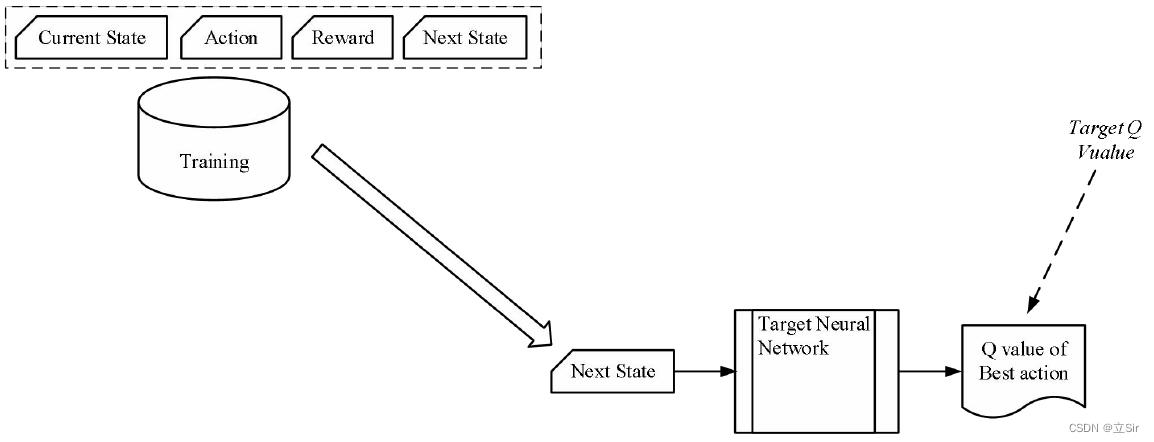
DQN 同时用到两个结构相同参数不同的神经网络，区别是一个用于训练，另一个不会在短期内得到训练，这样设置是从考虑实际效果出发的必然需求。

如果构建具有单个 Q 网络且不存在目标网络的 DQN，假设此网络应该如下工作：通过 Q 网络执行两次传递，首先输出 “预测 Q 值”，然后输出 “目标 Q 值”。这可能会产生一个潜在的问题：Q 网络的权重在每个时间步长都会更新，从而改进了对“预测 Q 值”的预测。但是，由于网络及其权重相同，因此它也改变了我们预测的“目标 Q 值”的方向。它们不会保持稳定，在每次更新后可能会波动，类似一直追逐一个移动着的目标。

通过采用第二个未经训练的网络，可以确保 “目标 Q 值” 至少在短时间内保持稳定。但这些“目标 Q 值”毕竟只是预测值，这是为改善它们的数值做出的妥协。所以在经过预先配置的时间步长后，需将 Q 网络中更新的权重复制到目标网络。

可以得出，使用目标网络可以带来更稳定的训练。

1.2.2 和 1.2.3 代码对应如下：

# -------------------------------------- #
# 构造深度学习网络，输入状态s，得到各个动作的reward
# -------------------------------------- #

class Net(nn.Module):
    # 构造只有一个隐含层的网络
    def __init__(self, n_states, n_hidden, n_actions):
        super(Net, self).__init__()
        # [b,n_states]-->[b,n_hidden]
        self.fc1 = nn.Linear(n_states, n_hidden)
        # [b,n_hidden]-->[b,n_actions]
        self.fc2 = nn.Linear(n_hidden, n_actions)
    # 前传
    def forward(self, x):  # [b,n_states]
        x = self.fc1(x)
        x = self.fc2(x)
        return x

# -------------------------------------- #
# 构造深度强化学习模型
# -------------------------------------- #

class DQN:
    #（1）初始化
    def __init__(self, n_states, n_hidden, n_actions,
                 learning_rate, gamma, epsilon,
                 target_update, device):
        # 属性分配
        self.n_states = n_states  # 状态的特征数
        self.n_hidden = n_hidden  # 隐含层个数
        self.n_actions = n_actions  # 动作数
        self.learning_rate = learning_rate  # 训练时的学习率
        self.gamma = gamma  # 折扣因子，对下一状态的回报的缩放
        self.epsilon = epsilon  # 贪婪策略，有1-epsilon的概率探索
        self.target_update = target_update  # 目标网络的参数的更新频率
        self.device = device  # 在GPU计算
        # 计数器，记录迭代次数
        self.count = 0

        # 构建2个神经网络，相同的结构，不同的参数
        # 实例化训练网络  [b,4]-->[b,2]  输出动作对应的奖励
        self.q_net = Net(self.n_states, self.n_hidden, self.n_actions)
        # 实例化目标网络
        self.target_q_net = Net(self.n_states, self.n_hidden, self.n_actions)

        # 优化器，更新训练网络的参数
        self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=self.learning_rate)

    #（3）网络训练
    def update(self, transition_dict):  # 传入经验池中的batch个样本
        # 获取当前时刻的状态 array_shape=[b,4]
        states = torch.tensor(transition_dict['states'], dtype=torch.float)
        # 获取当前时刻采取的动作 tuple_shape=[b]，维度扩充 [b,1]
        actions = torch.tensor(transition_dict['actions']).view(-1,1)
        # 当前状态下采取动作后得到的奖励 tuple=[b]，维度扩充 [b,1]
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1)
        # 下一时刻的状态 array_shape=[b,4]
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float)
        # 是否到达目标 tuple_shape=[b]，维度变换[b,1]
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1)

        # 输入当前状态，得到采取各运动得到的奖励 [b,4]==>[b,2]==>[b,1]
        # 根据actions索引在训练网络的输出的第1维度上获取对应索引的q值（state_value）
        q_values = self.q_net(states).gather(1, actions)  # [b,1]
        # 下一时刻的状态[b,4]-->目标网络输出下一时刻对应的动作q值[b,2]-->
        # 选出下个状态采取的动作中最大的q值[b]-->维度调整[b,1]
        max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1,1)
        # 目标网络输出的当前状态的q(state_value)：即时奖励+折扣因子*下个时刻的最大回报
        q_targets = rewards + self.gamma * max_next_q_values * (1-dones)

        # 目标网络和训练网络之间的均方误差损失
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
        # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        self.optimizer.zero_grad()
        # 反向传播参数更新
        dqn_loss.backward()
        # 对训练网络更新
        self.optimizer.step()

        # 在一段时间后更新目标网络的参数
        if self.count % self.target_update == 0:
            # 将目标网络的参数替换成训练网络的参数
            self.target_q_net.load_state_dict(
                self.q_net.state_dict())
        
        self.count += 1

DQN 模型伪代码：

---

2. 实例演示

接下来我们用 GYM 库中的车杆稳定小游戏来验证一下我们构建好的 DQN 模型，导入最基本的库，设置参数。有关 GYM 强化学习环境的内容可以查看官方文档：

https://www.gymlibrary.dev/#

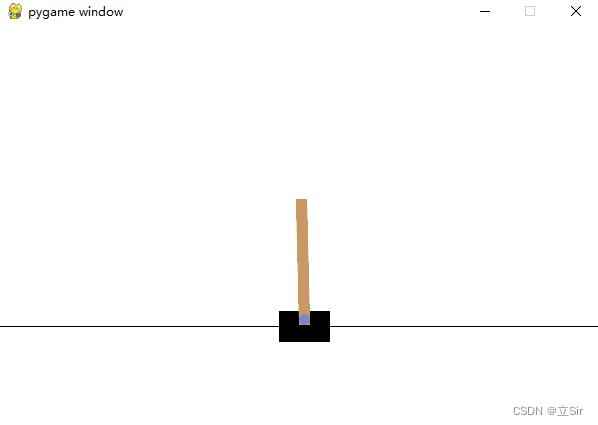
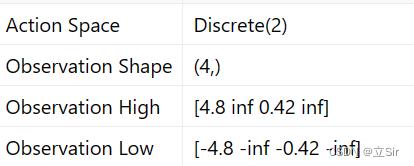
环境的状态 state 包含四个：位置、速度、角度、角速度；动作 action 包含 2 个：小车左移和右移；目的是保证杆子竖直。环境交互与模型训练如下：

import gym
from RL_DQN import DQN, ReplayBuffer
import torch
from tqdm import tqdm
import matplotlib.pyplot as plt

# GPU运算
device = torch.device("cuda") if torch.cuda.is_available() \\
        else torch.device("cpu")

# ------------------------------- #
# 全局变量
# ------------------------------- #

capacity = 500  # 经验池容量
lr = 2e-3  # 学习率
gamma = 0.9  # 折扣因子
epsilon = 0.9  # 贪心系数
target_update = 200  # 目标网络的参数的更新频率
batch_size = 32
n_hidden = 128  # 隐含层神经元个数
min_size = 200  # 经验池超过200后再训练
return_list = []  # 记录每个回合的回报

# 加载环境
env = gym.make("CartPole-v1", render_mode="human")
n_states = env.observation_space.shape[0]  # 4
n_actions = env.action_space.n  # 2

# 实例化经验池
replay_buffer = ReplayBuffer(capacity)
# 实例化DQN
agent = DQN(n_states=n_states,
            n_hidden=n_hidden,
            n_actions=n_actions,
            learning_rate=lr,
            gamma=gamma,
            epsilon=epsilon,
            target_update=target_update,
            device=device,
        )

# 训练模型
for i in range(500):  # 100回合
    # 每个回合开始前重置环境
    state = env.reset()[0]  # len=4
    # 记录每个回合的回报
    episode_return = 0
    done = False
    
    # 打印训练进度，一共10回合
    with tqdm(total=10, desc='Iteration %d' % i) as pbar:

        while True:
            # 获取当前状态下需要采取的动作
            action = agent.take_action(state)
            # 更新环境
            next_state, reward, done, _, _ = env.step(action)
            # 添加经验池
            replay_buffer.add(state, action, reward, next_state, done)
            # 更新当前状态
            state = next_state
            # 更新回合回报
            episode_return += reward

            # 当经验池超过一定数量后，训练网络
            if replay_buffer.size() > min_size:
                # 从经验池中随机抽样作为训练集
                s, a, r, ns, d = replay_buffer.sample(batch_size)
                # 构造训练集
                transition_dict = 
                    'states': s,
                    'actions': a,
                    'next_states': ns,
                    'rewards': r,
                    'dones': d,
                
                # 网络更新
                agent.update(transition_dict)
            # 找到目标就结束
            if done: break
        
        # 记录每个回合的回报
        return_list.append(episode_return)

        # 更新进度条信息
        pbar.set_postfix(
            'return': '%.3f' % return_list[-1]
        )
        pbar.update(1)

# 绘图
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
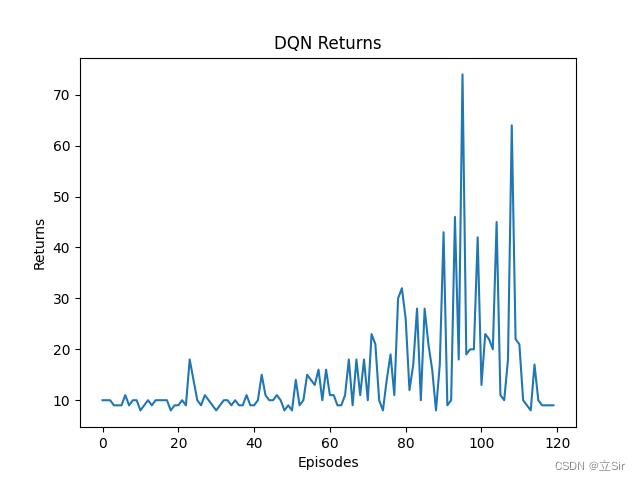
plt.title('DQN Returns')
plt.show()

我简单训练了100轮，每回合的回报 returns 绘图如下。若各位发现代码有误，请及时反馈。