js两个数字求和？求高手留下

Posted 2023-03-23

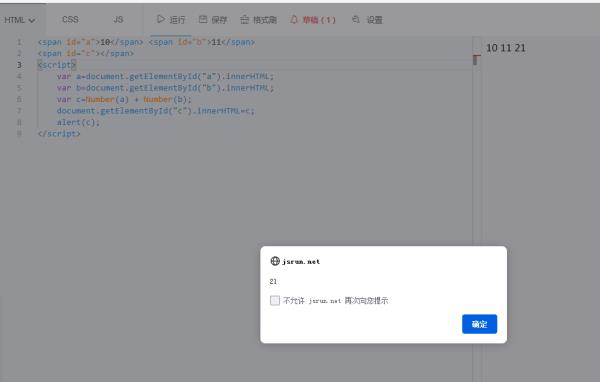
比如我有2个 <span id="a">10<span> <span id="b">11<span>想得出结果<span id="c">21<span>
就是把a和b相加等于3，这个js怎么写

用纯js的话下面这样写：

<span id="a">10</span> <span id="b">11</span>

<span id="c"></span>

<script>

   var a=document.getElementById("a").innerhtml;

   var b=document.getElementById("b").innerHTML;

   var c=Number(a) + Number(b);

   document.getElementById("c").innerHTML=c;

</script>

parseFloat或者parseInt转换下，不然会当做字符串拼接的。我们这里用的Number来转换，此外还有parseFloat或者parseInt这两个转换函数。

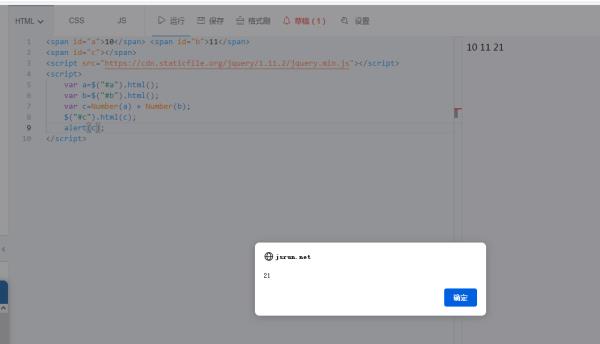
另外，如果你会jQuery的话获取字符串内容那儿可以更加简单点。

<script>

   var a=$("#a").html();

   var b=$("#b").html();

   var c=Number(a) + Number(b);

   $("#c").html(c);

</script>

参考技术A let a=document.getElementById("a").innerHTML；
let b=document.getElementById("b").innerHTML；
let c=Number(a) + Number(b)；
这样再把结果给c就好了，通常数学运算需要把字符串转换成数字才行，不然会被当成字符串拼接，希望能帮到你。 参考技术B 求和就跟数学一样，直接相加就可以了啊。
我猜你的问题出在获取span的内容上，如果你直接用 a.innerHTML + b.innerHTML ，得到的不是21，而是1011。
原因并不是因为 js 中不能直接进行加法运算，而是因为数据类型导致。
要记住一点：所有通过标签获取到的内容，都是字符串。
也就是说，通过标签的， value, innerHTML 等得到的值，都是一个字符串值，而js中，用加号来对字符串进行求和，实际是做字符串连接。比如 '1' + '2' ，得到的是 '12'，而不是3. 因为加号左右都是字符串。在js 中，只要加号的任何一边的值是字符串，最终都是进行字符串连接，而不是求和。
想要实现求和，就需要把字符串变成数字，再使用加号，在js中，将字符串变成数字最简单的做法是乘以1，比如 '1'*1 + '2'*1 ，结果就是3了。这个属于JS的隐式类型转换，如果你学过这个知识点，自然知道是什么意思 ，如果还没学过，那就先知道这个技巧就行。
所以你上面的效果，要实现求和，只需要这样：
a.innerHTML * 1 + b.innerHTML * 1， 就可以实现求和啦。

求C语言高手！

#include<stdio.h>
#include<string.h>
struct employee
int num; //编号
char name[20]; //姓名
char sex[20]; //性别
int age; //年龄
char job[20]; //职务
char dep[50]; //部门
employee[50];
void addemp()
char c[2];
do

int n=0;
printf("姓名\n");
scanf("%s",&employee[n].name);
printf("性别\n");
scanf("%s",&employee[n].sex);
printf("编号\n");
scanf("%d",&employee[n].num);
printf("年龄\n");
scanf("%d",&employee[n].age);
printf("职务\n");
scanf("%s",&employee[n].job);
printf("部门\n");
scanf("%s",&employee[n].dep);
n++;
printf("添加下一员工信息，请按y\n");
scanf("%s",&c);

while(!(strcmp(c,"y")));

void showemp()
int i;
printf(" 编号 姓名 性别 年龄 职务 部门 \n");
for(i=1;employee[i].num!=0;i++);

printf("%d",employee[i].num);
printf("%s %s ",employee[i].name,employee[i].sex);
printf("%d ",employee[i].age);
printf("%s %s",employee[i].job,employee[i].dep);



void search_sex()
char a[20];
int i;
printf("输入性别\n");
scanf("%s",&a);
for(i=0;i<50;i++)
if(strcmp(a,employee[i].sex)==0)
printf(" 编号 姓名 性别 年龄 职务 部门 \n %d %s %s %d %s %s",employee[i].num,employee[i].name,employee[i].sex,employee[i].age,employee[i].job,employee[i].dep);


void search_dep()
char b[20];
int i;
printf("输入职务\n");
scanf("%s",&b);
for(i=0;i<50;i++)
if(strcmp(b,employee[i].dep)==0)
printf(" 编号 姓名 性别 年龄 职务 部门 \n%d %s %s %d %s %s",employee[i].num,employee[i].name,employee[i].sex,employee[i].age,employee[i].job,employee[i].dep);


void main()
int i;
for (i=0;i<50;i++)
printf("*");
printf("\n 员工信息管理系统\n");
printf (" 通信二班--刘尧\n");

printf("@ 0 退出员工信息管理系统。 @\n");
printf("@ 1 输入员工信息 @\n");
printf("@ 2 显示所有员工信息 @\n");
printf("@ 3 查找某部门员工信息 @\n");
printf("@ 4 查找男女员工信息 @\n");
for(i=0;i<50;i++)
printf("*");
printf("\n");
//菜单页面
int n;
scanf("%d",&n);
for(i=1;i!=0;i++)
switch(n)
case 1:addemp();printf("\n");break;
case 2:showemp();printf("\n");break;
case 3:search_dep();printf("\n");break;
case 4:search_sex();printf("\n");break;
default:printf("输入有误，请重新输入\n");

printf("请输入下一项操作代码，否则按0退出\n");
scanf("%d",&n);

Numerical Recipes in C
一书及所附程序，有完整程序。不过我封装了它的C++版本，可以对但参数或多参数求极值，完整的头文件为：

#ifndef __OPTIMIZATION_H__
#define __OPTIMIZATION_H__

//////////////////////////////////////////////////////////////////////////
// class TOptimization
//
// $ 求函数一个或多个参数的最小值
//
// 该类默认对一个参数优化，一般只要输入优化参数数目
// 优化目标函数就可以使用。
//
// ...主要代码来自：
// Numerical Recipes in C++
// The Art of Scientific Computing
// Second Edition
// William H. Press Saul A. Teukolsky
// William T. Vetterling Brian P. Flannery
//
// 中译本：
// C++ 数值算法(第二版) 胡健伟 赵志勇 薛运华 等译
// 电子工业出版社 北京 (2005)
//
// Author: Jian Feng
// Email: [e-mail]
// Dec. 9, 2006
//
//////////////////////////////////////////////////////////////////////////
//
// 输入函数：
//
// @MaxIterationStep: 最大迭代次数， 默认 1000
// @ParameterNumbers: 优化参数数目， 默认 1
// @InitMatrix: 初始化矩阵参数(N*N)， 默认
// @Tolerance: 容许公差， 默认 1E-7
//
// 执行函数：
//
// @ExecutePowell: 利用powell方法进行多参数优化
// @ExecuteBrent: 利用brent方法进行单参数优化
//
// 输出函数：
//
// @OptimizatedParameters: 优化结果数据
// @ObjectiveFunctionValue: 目标函数在优化值处的值
//
// 使用示例：
//
// 1. 单参数
// double objfun(double a)
// double sum = 0;
// for(int i = 0; i < DataPoints; ++i)
// sum += SQR(Exps[i] - Theo(a));
//
// double value
// TOptimization opt;
// if(opt.ExecuteBrent(objfun, -10, -1)) opt.OptimizatedParameters(&value);
//
// 2. 多参数
// double objfun(double *a)
// double sum = 0;
// for(int i = 0; i < DataPoints; ++i)
// sum += SQR(Exps[i] - Theo(a));
//
// double value[3]
// TOptimization opt(3);
// double ival[3] = ;
// if(opt.ExecutePowell(objfun, ival)) opt.OptimizatedParameters(value);
//
namespace
static int ncom; //公用变量
static double *pcom_p; //公用变量
static double *xicom_p; //公用变量
static double (*nrfunc)(double*); //公用函数指针


class TOptimization

private:
typedef double (*Reff)(double *);
typedef double (*Ptrf)(double );

public:
TOptimization(int n = 1);
~TOptimization()

//主要方法
void ParameterNumbers(int n)

//利用powell方法对一个或多个参数优化
bool ExecutePowell(Reff obj, double *a = 0);

//利用brent方法对一个参数优化，需给出参数所在的区间
bool ExecuteBrent(Ptrf obj, double vFrom = 0, double vTo = 1);

void OptimizatedParameters(double *a)

void OptimizatedParameters(double &a)

//void OptimizatedParameters(double *a)
// if(method) for(int i=0; i<num; ++i) a[i]=coef[i];
// else *a = vmin;
//

//其它方法
void InitMatrix(double **m)

for(int i=0; i<num; ++i)
for(int j = 0; j<num; ++j)
matx[i][j]=m[i][j];
setm = true;


void MaxIterationStep(int s)

void Tolerance(double eps)

double ObjectiveFunctionValue()const

private:

double brent(double ax, double bx, double cx, Ptrf f, double tol, double &xmin, int &flag);
void mnbrak(double &ax, double &bx, double &cx, double &fa, double &fb, double &fc, Ptrf func);
void linmin(double *p, double *xi, double &fret, Reff func);
bool powell(double *p, double **xi, double ftol, int &iter, double &fret, Reff func);

void shft2(double &a, double &b, const double c)

void shft3(double &a, double &b, double &c, const double d)

double SQR(double x)

void SWAP(double &a, double &b)

double SIGN(const double &a, const double &b)

double MAX(const double &a, const double &b)

void AllocateMemory();

void FreeMemory();

static double f1dim(double x)

int j;
double *xt = new double [ncom];
//Vec_Dp &pcom=*pcom_p,&xicom=*xicom_p;
double *pcom = pcom_p, *xicom = xicom_p;
for (j=0;j<ncom;j++)
xt[j]=pcom[j]+x*xicom[j];
//delete []xt;
double val = nrfunc(xt);
delete []xt;
return val;


bool setm; //是否设置优化方向初始矩阵

int num; //优化参数
int ITMAX; //最大迭代数
int iter; //实际迭代步数
int method; //优化方法 0: 1-D brent, 2: M-D Powell

double vmin; //一维优化参数
double ftol; //容许差
double fret; //目标函数值

double *coef; //多维优化参数值
double **matx; //多维优化参数方向的初始值

;

//////////////////////////////////////////////////////////////////////////

inline TOptimization::TOptimization(int n )

num = n;
ftol = 1e-7;
ITMAX = 1000;
iter = 0;
fret = 0.;
vmin = 0.;
method = 0;
setm = false;

AllocateMemory();


inline void TOptimization::AllocateMemory()

pcom_p = new double [num];
xicom_p = new double [num];
coef = new double [num];
matx = new double *[num];
for(int i = 0; i < num; ++i)

coef[i] = 0.;
matx[i] = new double [num];
for(int j = 0; j < num; ++j)
matx[i][j]=(i == j ? 1.0 : 0.0);



inline void TOptimization::FreeMemory()

for(int i = 0; i < num; ++i)

delete []matx[i];

delete []matx;
delete []pcom_p;
delete []xicom_p;
delete []coef;


inline bool TOptimization::ExecutePowell(Reff obj, double *a)

method = 1;
if(a)
for(int i = 0; i < num; ++i) coef[i] = a[i];
return powell(coef, matx, ftol, iter, fret, obj);


inline bool TOptimization::ExecuteBrent(Ptrf obj, double vFrom, double vTo)

method = 0;
int flag;
double cx, fa, fb, fc;
mnbrak(vFrom,vTo,cx,fa,fb,fc,obj);
fret = brent(vFrom,vTo,cx,obj, ftol,vmin, flag);
return flag ? true : false;


inline void TOptimization::mnbrak(double &ax, double &bx, double &cx, double &fa,
double &fb, double &fc, Ptrf func)

const double GOLD=1.618034,GLIMIT=100.0,TINY=1.0e-20;
double ulim,u,r,q,fu;

fa=func(ax);
fb=func(bx);
if (fb > fa)
SWAP(ax,bx);
SWAP(fb,fa);

cx=bx+GOLD*(bx-ax);
fc=func(cx);
while (fb > fc)
r=(bx-ax)*(fb-fc);
q=(bx-cx)*(fb-fa);
u=bx-((bx-cx)*q-(bx-ax)*r)/
(2.0*SIGN(MAX(fabs(q-r),TINY),q-r));
ulim=bx+GLIMIT*(cx-bx);
if ((bx-u)*(u-cx) > 0.0)
fu=func(u);
if (fu < fc)
ax=bx;
bx=u;
fa=fb;
fb=fu;
return;
else if (fu > fb)
cx=u;
fc=fu;
return;

u=cx+GOLD*(cx-bx);
fu=func(u);
else if ((cx-u)*(u-ulim) > 0.0)
fu=func(u);
if (fu < fc)
shft3(bx,cx,u,cx+GOLD*(cx-bx));
shft3(fb,fc,fu,func(u));

else if ((u-ulim)*(ulim-cx) >= 0.0)
u=ulim;
fu=func(u);
else
u=cx+GOLD*(cx-bx);
fu=func(u);

shft3(ax,bx,cx,u);
shft3(fa,fb,fc,fu);



inline double TOptimization::brent(double ax, double bx, double cx,
Ptrf f, double tol, double &xmin, int &flag)

flag = 1;
const double CGOLD=0.3819660;
const double ZEPS=1.0e-20;
int iter;
double a,b,d=0.0,etemp,fu,fv,fw,fx;
double p,q,r,tol1,tol2,u,v,w,x,xm;
double e=0.0;

a=(ax < cx ? ax : cx);
b=(ax > cx ? ax : cx);
x=w=v=bx;
fw=fv=fx=f(x);
for (iter=0;iter<ITMAX;iter++)
xm=0.5*(a+b);
tol2=2.0*(tol1=tol*fabs(x)+ZEPS);
if (fabs(x-xm) <= (tol2-0.5*(b-a)))
xmin=x;
return fx;

if (fabs(e) > tol1)
r=(x-w)*(fx-fv);
q=(x-v)*(fx-fw);
p=(x-v)*q-(x-w)*r;
q=2.0*(q-r);
if (q > 0.0) p = -p;
q=fabs(q);
etemp=e;
e=d;
if (fabs(p) >= fabs(0.5*q*etemp) || p <= q*(a-x) || p >= q*(b-x))
d=CGOLD*(e=(x >= xm ? a-x : b-x));
else
d=p/q;
u=x+d;
if (u-a < tol2 || b-u < tol2)
d=SIGN(tol1,xm-x);

else
d=CGOLD*(e=(x >= xm ? a-x : b-x));

u=(fabs(d) >= tol1 ? x+d : x+SIGN(tol1,d));
fu=f(u);
if (fu <= fx)
if (u >= x) a=x; else b=x;
shft3(v,w,x,u);
shft3(fv,fw,fx,fu);
else
if (u < x) a=u; else b=u;
if (fu <= fw || w == x)
v=w;
w=u;
fv=fw;
fw=fu;
else if (fu <= fv || v == x || v == w)
v=u;
fv=fu;



flag = 0;
xmin=x;
return fx;


inline void TOptimization::linmin(double *p, double *xi, double &fret, Reff func)

int j, flag;
const double TOL=1.0e-8;
double xx,xmin,fx,fb,fa,bx,ax;

int n=num;
ncom=n;
//pcom_p=new Vec_Dp(n);
//xicom_p=new Vec_Dp(n);
nrfunc=func;
//Vec_Dp &pcom=*pcom_p,&xicom=*xicom_p;
double *pcom = pcom_p, *xicom = xicom_p;
for (j=0;j<n;j++)
pcom[j]=p[j];
xicom[j]=xi[j];

ax=0.0;
xx=1.0;
mnbrak(ax,xx,bx,fa,fx,fb,f1dim);
fret=brent(ax,xx,bx,f1dim,TOL,xmin, flag);
for (j=0;j<n;j++)
xi[j] *= xmin;
p[j] += xi[j];

//delete xicom_p;
//delete pcom_p;


inline bool TOptimization::powell(double *p, double **xi, double ftol, int &iter,
double &fret, Reff func)

const int ITMAX=500;
const double TINY=1.0e-20;
int i,j,ibig;
double del,fp,fptt,t;

int n=num;
//Vec_Dp pt(n),ptt(n),xit(n);
double *pt, *ptt, *xit;
for(i = 0; i < n; ++i)

pt = new double [n];
ptt = new double [n];
xit = new double [n];

fret=func(p);
for (j=0;j<n;j++) pt[j]=p[j];
for (iter=0;;++iter)
fp=fret;
ibig=0;
del=0.0;
for (i=0;i<n;i++)
for (j=0;j<n;j++) xit[j]=xi[j][i];
fptt=fret;
linmin(p,xit,fret,func);
if (fptt-fret > del)
del=fptt-fret;
ibig=i+1;


if (2.0*(fp-fret) <= ftol*(fabs(fp)+fabs(fret))+TINY)
delete []pt;
delete []ptt;
delete []xit;
return true;

if (iter == ITMAX)

delete []pt;
delete []ptt;
delete []xit;
return false;
//cerr<<"powell exceeding maximum iterations.";

for (j=0;j<n;j++)
ptt[j]=2.0*p[j]-pt[j];
xit[j]=p[j]-pt[j];
pt[j]=p[j];

fptt=func(ptt);
if (fptt < fp)
t=2.0*(fp-2.0*fret+fptt)*SQR(fp-fret-del)-del*SQR(fp-fptt);
if (t < 0.0)
linmin(p,xit,fret,func);
for (j=0;j<n;j++)
xi[j][ibig-1]=xi[j][n-1];
xi[j][n-1]=xit[j];






#endif
参考技术A 1、void showemp()函数中for(i=1;employee[i].num!=0;i++);
循环应该从i=0开始啊~~不知道你不能显示出来的员工信息有多少，如果是这个原因，只会少显示1个。

2、void search_dep() 开起来没问题，只是你申请的b[20]和前面结构体中申明的dep[50]不一样，改过来看看能不查找~~~ 参考技术B 问题是什么？追问

程序不能显示所有员工信息，不能按职务查找，但能按性别查找。拜托了……