ARMA模型性质之平稳AR模型得统计性质
Posted 洋洋菜鸟
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了ARMA模型性质之平稳AR模型得统计性质相关的知识，希望对你有一定的参考价值。
目录
1.均值
如果AR(p)模型满足平稳性条件，则
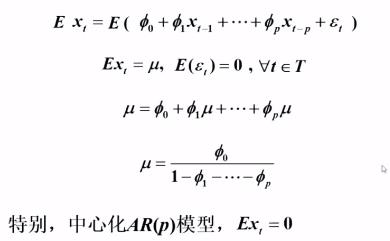
Green函数定义
AR模型得传递形式：
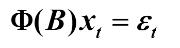
因为均值的性质，则有：
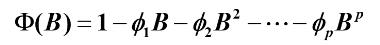
则，求得Xt 为
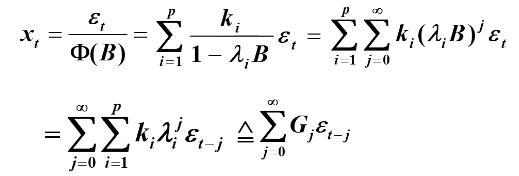
则有Green函数：
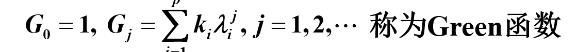
记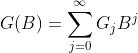 
则模型可简记为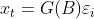 
Green函数递推公式
因为：
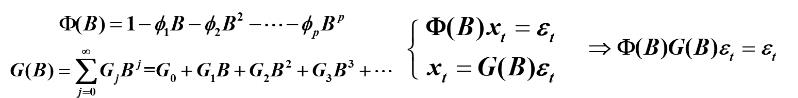
则有：
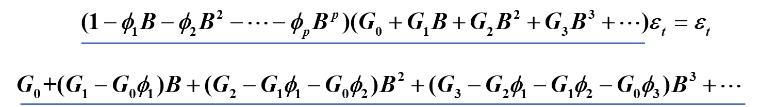
再可解得：
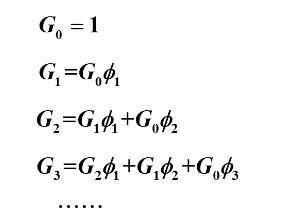
则有得出规律公式为：
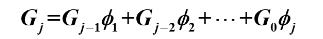
则有总结如下：
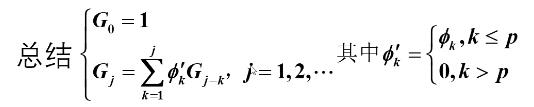
2.方差
平稳AR模型得传递形式
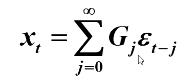
两边求方差得
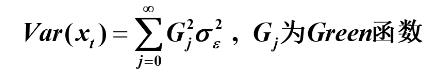
举例：
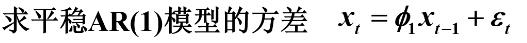
方法1：
根据Green函数：
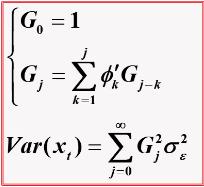
可求得如下：
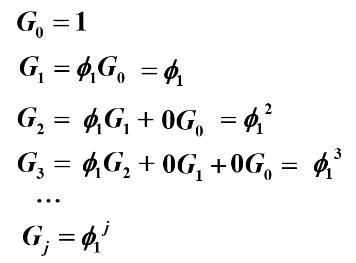
最后得出平稳AR(1)模型的方差
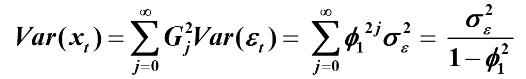
方法2：
平稳AR(1) 模型
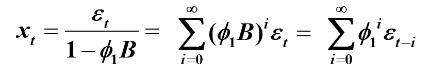
两边求方差
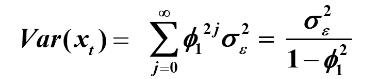
AR(2)模型的方差为：
利用Green 函数可以推导出 AR(2) 模型的方差为：
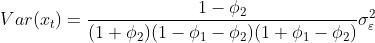
3.协方差函数
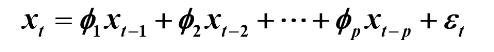
两边求期望得：
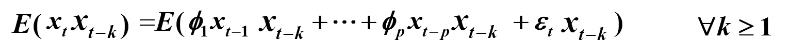
又因为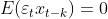 
可得到协方差函数得递推公式
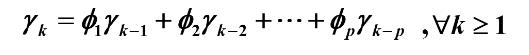
举例1：
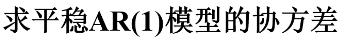
AR(1)模型为：
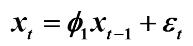
递推公式：
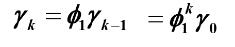
因为 平稳AR(1)模型 具有如下：
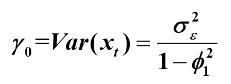
则可得该协方差函数递推公式为：
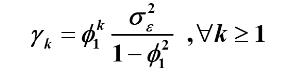
举例2：
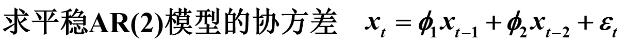
协方差函数递推公式
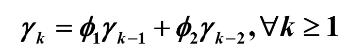
令 k = 1 可得：
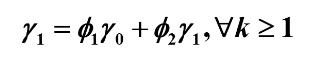
于是可得如下结论：
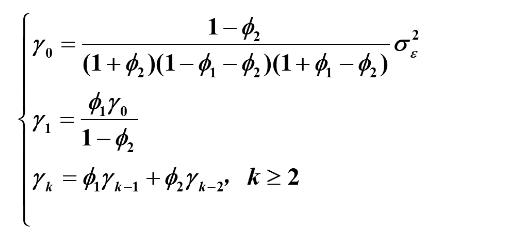
4.自相关系数
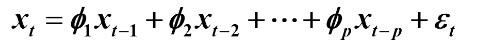
通过上式，可得到下式：
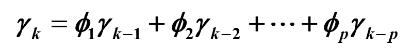
则自相关系数得定义为
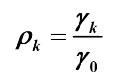
则有平稳AR(P)模型的自相关系数递推公式
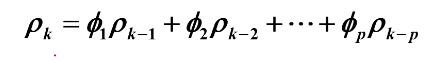
常用的ARA模型自相关系数递推公式：
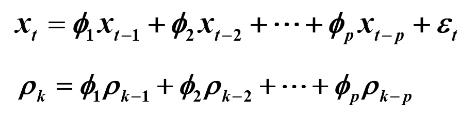
其中 AR(1)模型为
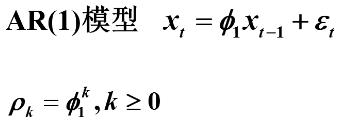
AR(2)模型为
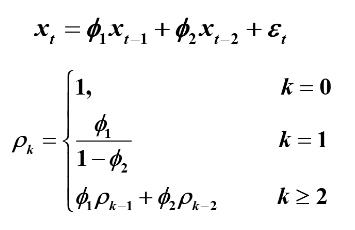
AR模型自相关系数的性质
模型：
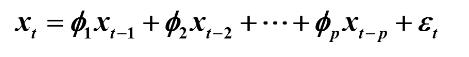
得齐次差分方程：
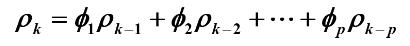
设通解形式为
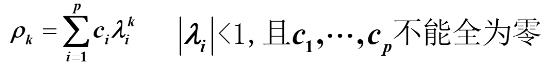
呈指数衰减
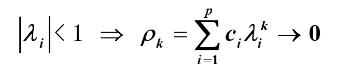
性质：拖尾性*：
举例
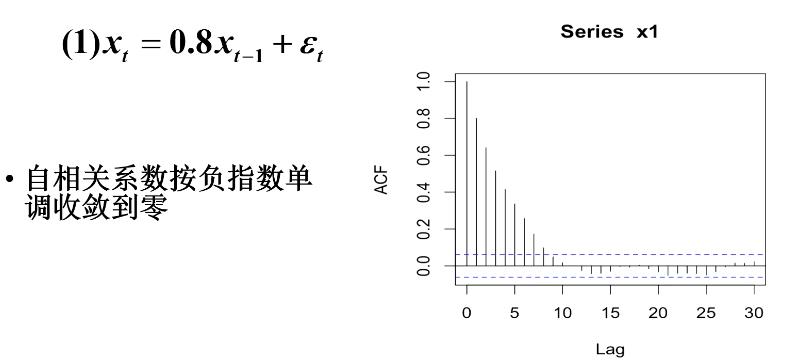
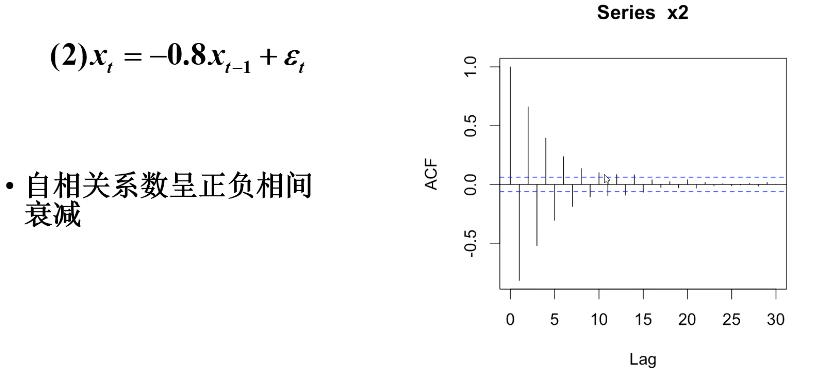
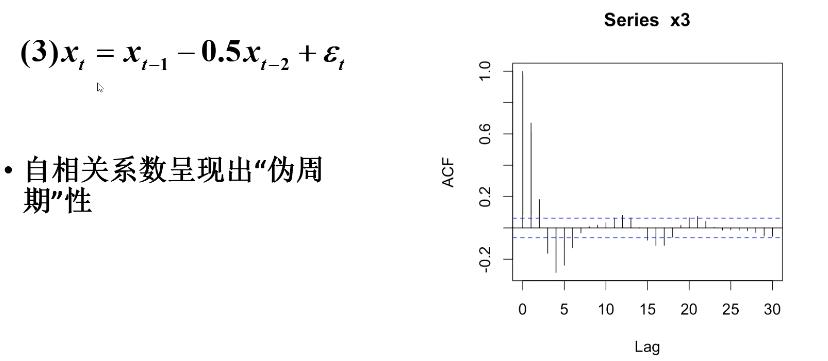
5.偏自相关系数
定义：
对于平稳AR(p)序列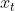
，所谓滞后k偏自相关系数就是指在给定中间 k-1 个随机变量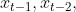 
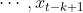的条件下，或者说，在剔除了中间 k-1 个随机变量的干扰之后，
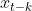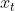对 影响的相关度量。用数学语言描述就是
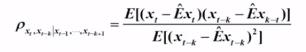
其中：
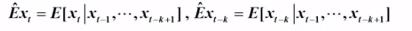
偏相关系数的计算：
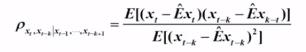
用过去的k期序列值对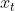作k阶自回归拟合：此为式1
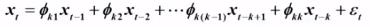
取条件期望：此为式2
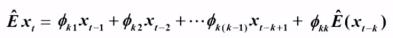
1式 - 2式 ：
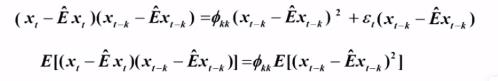
Yule - Walker 方程组：
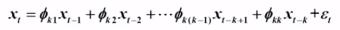
两边同时乘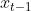 
，取期望 ：
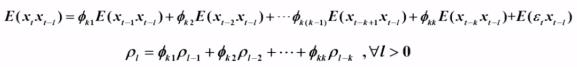
取前 k 个构成 Yule - Walker 方程组 ：
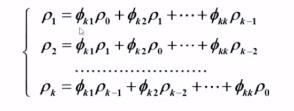
解方程组可得可得延迟k偏自相关系数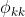 
Yule - Walker 方程求解：
Yule - Walker 方程写成矩阵形式为：
根据 Cramer 法则：
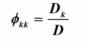
其中
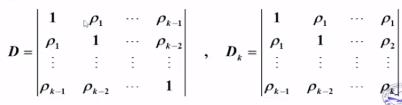
AR模型偏相关系数的截尾性
AR模型：
自相关系数：
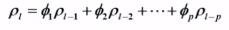
Yule - Walker 方程成立：
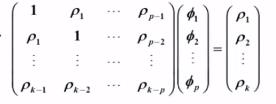
当 p>k 时：
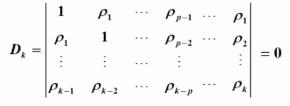
则有：
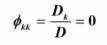
再讲一下AR模型的具体偏相关系数的解：
AR(1)模型：
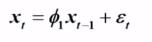
Yule - Walker 方程：
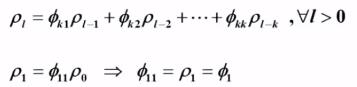
偏自相关系数的解：
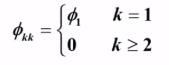
AR(2)模型：
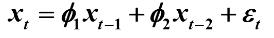
Yule - Walker 方程：
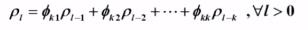
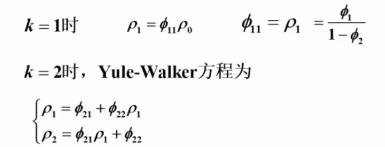
对 AR(2) 模型又有：
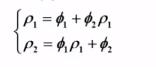
从而得到偏自相关系数的解：
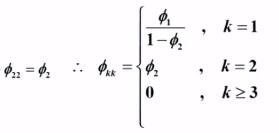
举例：
例1：
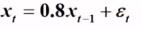
根据 AR(1) 模型的偏相关系数的解：
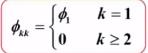
可得该问题的偏相关系数为：
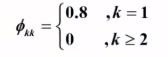
例2：
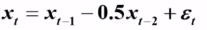
根据 AR(2) 模型的偏相关系数的解：
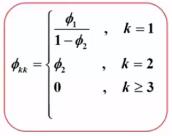
可得该问题的偏相关系数为：
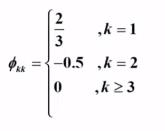
总结：
平稳AR模型得统计性质：
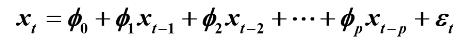
1.均值
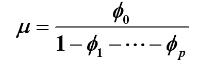
2.方差
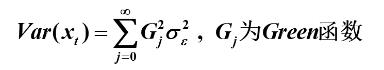
3.协方差函数
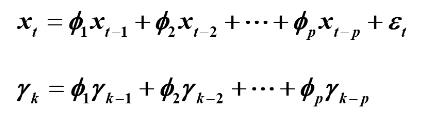
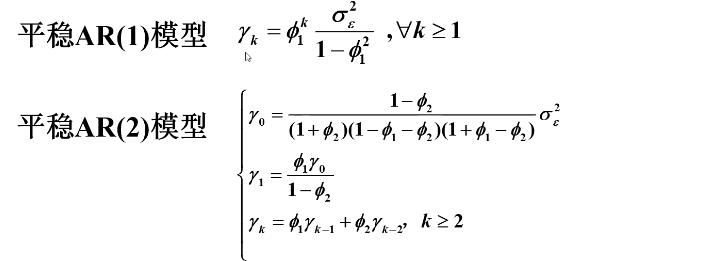
4.自相关系数
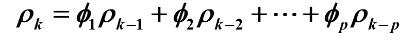
常用得AR模型自相关系数递推公式
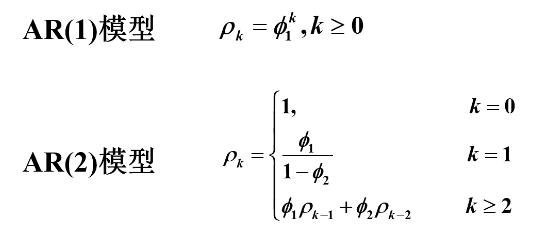
AR模型自相关系数的性质： 拖尾性
猿创征文｜时间序列分析算法之平稳时间序列预测算法和自回归模型(AR)详解+Python代码实现
目录
二、自回归模型(Autoregressive model,简称AR)
前言
平滑法花费了将近一个月的时间去讲解和模拟算法，讲解的非常详细了我个人认为，而且代码和原理理解起来也相对简单，代码实现起来也几乎没有什么难度。若是没有大家想要详细了解或者掌握时间序列分析算法的建议可以订阅本人专栏：一文速学-数学建模常用模型。里面涉及到各个场景的分析和预测模型基本都具备了，其中平滑法的所有方法：
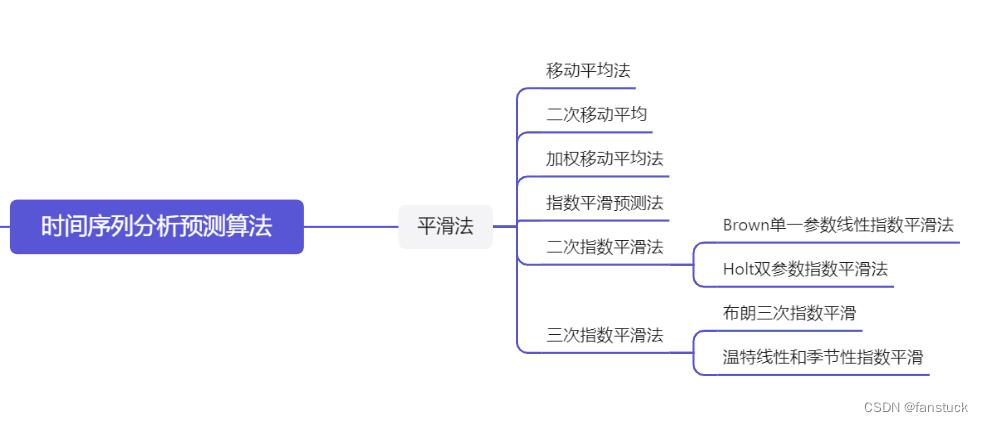
都包含其中。接下来我们要对平稳时间序列预测算法进行研究和推导。但是平稳时间序列预测算法的基础理论还是蛮多蛮复杂的，需要我们对基础理论有了一定认知才能更轻松的掌握该算法。故我们的开篇第一章先将理论知识全部了解一遍。
希望读者看完能够在评论区提出错误或者看法，博主会长期维护博客做及时更新。
一、平稳时间序列预测算法
这里的平稳是指宽平稳，其特性是序列的统计特性不随时间的平移而变化，即均值和协方差不随时间的平移而变化。 时间序列是指将某种现象某一个统计指标在不同时间上的各个数值，按时间先后顺序排列而形成的序列。平稳时间序列粗略地讲，一个时间序列，如果均值没有系统的变化（无趋势）、方差没有系统变化，且严格消除了周期性变化，就称之是平稳的。
平稳时间序列是时间序列分析中最重要的特殊类型。到目前为止，时间序列分析基本上是以平稳时间序列为基础的，对于非平稳时间序列的统计分析，其方法和理论都很有局限性。
这里我们需要了解关于时间序列的基本属性以及相应点的分布：
1.时间序列的分布、均值和协方差函数
概率分布
由于确定时间序列的分布函数一般不可能，人们更加注意使用时间序列的各种特征量的描述，如均值函数、协方差函数、自相关函数、偏自相关函数等，这些特征量往往能代表随机变量的主要特征。
均值函数
一个时间序列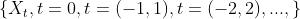
的均值函数指：
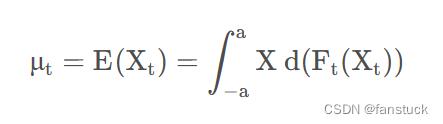
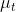即为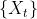
的均值函数，它实质上是一个实数列，均值表示随机过程在各个时刻的摆动中心。
自协方差函数
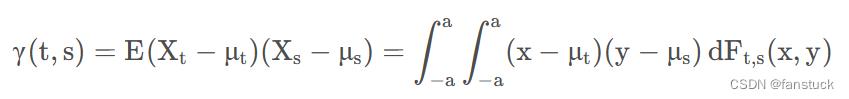
对称性: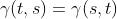
自相关函数
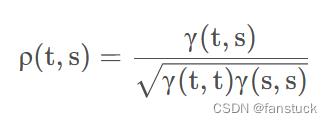
自相关函数描述了时间序列的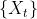自身的相关结构。时间序列的自相关函数具有对称性，且有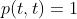
2.平稳序列的自协方差和自相关函数
自协方差函数
若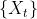为平稳序列，假定
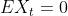,则我们可以用以下记号表示平稳序列的自协方差函数：
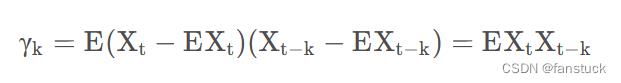
自相关函数
相应的，严平稳序列的自相关函数记为:
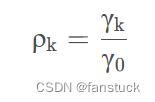
平稳序列的自协方差序列和自相关函数列的性质
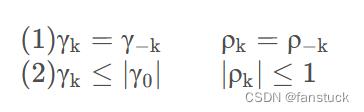
平稳时间序列分为严平稳时间序列与宽平稳时间序列。
3.严平稳时间序列
若对于时间t的任意n个值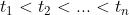
，序列中的随机变量
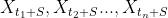联合分布与整数S无关，即有：
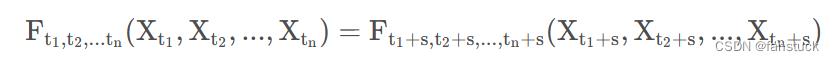
则称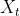
为严平稳/狭义平稳/强平稳时间序列。严平稳的概率分布与时间无关。
4.宽平稳时间序列
如时间序列有有穷的二阶矩阵，且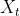满足以下两个条件：
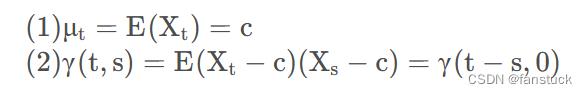
则称该时间序列为宽平稳过程。
宽平稳过程各随机变量的均值为常数，且任意两个变量的协方差仅与时间间隔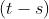
有关。
5.联系和区别
联系
- 若一个序列为严平稳序列，且有有穷的二阶矩阵，那么该序列也必为宽平稳序列。
- 若时间序列为正态序列(即它的任何有限维分布都是正态分布)，那么该序列为严平稳序列和宽平稳序列是相互等价的。
区别
- 严平稳的概率分布随时间的平移而不变，宽平稳序列的均值和自协方差随时间的平移而不变。
- 一个严平稳序列，不一定是宽平稳序列;一个宽平稳序列也不一定是严平稳序列。
实际中讨论的平稳时间序列是宽平稳时间序列，指对任意时间下，序列的均值、方差存在并为常数，且自协方差函数与自相关系数只与时间间隔k有关。只有平稳时间序列才可以进行统计分析，因为平稳性保证了时间序列数据都是出自同一分布。可以使用单位根检验来检验时间序列的平稳性。
若一个平稳时间序列的序列值之间没有相关性，那么就意味着这种数据前后没有规律，也就无法挖掘出有效的信息，这种序列称为纯随机序列。在纯随机序列中，有一种序列称为白噪声序列，这种序列随机且各期的方差一致。平稳时间序列分析在于充分挖掘时间序列之间的关系，当时间序列中的关系被提取出来后，剩下的序列就应该是个白噪声序列。
6.白噪声序列
定义
若时间序列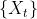满足下列性质：
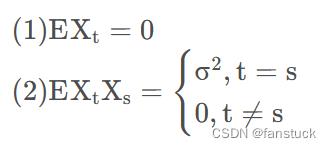
则称此序列为白噪声序列。
白噪声序列是一种特殊的宽平稳序列，也是一种最简单的平稳序列。
7.独立同分布序列
定义
如果时间序列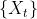中的随机变量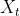是相互独立的随机变量，且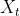具有相同的分布（当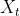有一阶矩时，往往还假定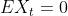),则称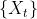为独立同分布序列。
独立同分布序列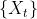是一个严平稳序列
一般来说，白噪声序列与独立同分布序列是不同的两种序列。
但是当白噪声序列为正态序列时，它也是独立同分布序列，此时我们称其为正态白噪声序列。
二、自回归模型(Autoregressive model,简称AR)
定义
自回归模型是统计上一种处理时间序列的方法，用同一变数例如x的之前各期，亦即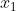
至
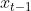来预测本期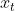
的表现，并假设它们为一线性关系。因为这是从回归分析中的线性回归发展而来，只是不用x预测y，而是用x预测 x(自己);所以叫做自回归。
p阶自回归模型的自相关系数拖尾，偏自相关系数p阶截尾。
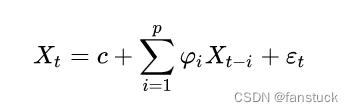
其中:c是常数项；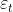
被假设为平均数等于0，标准差等于
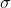的随机误差值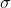；被假设为对于任何的t都不变。
文字叙述为：X的期望值等于一个或数个落后期的线性组合，加常数项，加随机误差。
建模步骤
第一步：
对时间蓄力进行白噪音检测，若经检验判定序列为白噪声，则这种数据前后没有规律，也就无法挖掘出有效的信息。只有检测不是白噪音序列才能继续。
第二步：
对序列作平稳性检验，若经检验判定为非平稳，则进行序列的平稳化处理，转第一步；否则转第三步；
第三步：
对模型进行识别，估计其参数，转第四步；
第四步：
检验模型的适用性，若检验通过，则得到拟合模型并可对序列做预测；否则转第三步；
模型判定
对于观测到的时间序列，若通过白噪音检测确定是非白噪音，且经平稳性检验后确定为平稳后，常根据相关系数和偏相关系数来识别模型。判断该问题是否适用AR模型建模，以及大致确定阶数p。
通过计算自相关系数SAF，和偏相关系数PACF。
如果一个时间序列满足以下两个条件:
- ACF 具有拖尾性，即 ACF(k) 不会在 k 大于某个常数之后就恒等于 0。
- PACF 具有截尾性，即 PACF(k) 在 k>p 时变为 0。（用来确定阶数， PACF 在 p 阶延迟后未必严格为 0 ，而是在 0 附近的小范围内波动）
那么就可以尝试使用AR模型。
案例实现
Python中用statsmodels.tsa.ar_model包中的AutoReg来实现自回归。
from statsmodels.tsa.ar_model import AutoReg该类函数参数为：
ar_model = AutoReg(endog,
lags,
trend='c',
seasonal=False,
exog=None,
hold_back=None,
period=None,
missing='none',
*,
deterministic=None,
old_names=False)这里不展开一一讲解，想要详细了解的可以去看官方解释:
statsmodels.tsa.ar_model.AutoReg — statsmodels
通常情况下只需要输入序列endog和阶数lags：
endog:接受类型为数组类型，一维时间序列。
lags:模型阶数，如果是整数，则模型中包含的滞后数或要包含的滞后指数列表。例如，[1，4]将只包括lags为1和4，而lags=4将包括滞后1、2、3和4。
from statsmodels.tsa.ar_model import AutoReg
import numpy as np
# 生成N(0,1)随机正态分布（白噪声）
noise = np.random.randn(200)
wnoise = (noise-np.mean(noise))/np.std(noise)
# 生成AR(2)线性序列 X(t)=0.5X(t-1)+0.1X(t-2)
X = [20,10] # 初值
for i in range(200):
x2 = 0.5*X[i+1]+0.1*X[i]+wnoise[i]
X.append(x2)
# 2阶AR模型拟合（OLS）
AR2_model = AutoReg(X, 2).fit()
# 模型预测第3到第202个时间点的数据
predict = AR2_model.predict(2,201)
# 计算残差
residual = X[2:]-predict我们模拟生成了AR线性蓄力之后，再进行AR2阶拟合得到预测值，之后使用matplotlib展示 ：
import matplotlib.pyplot as plt
plt.figure()
plt.subplot(311)
plt.plot(X[2:])
plt.subplot(312)
plt.plot(predict)
plt.subplot(313)
plt.plot(residual)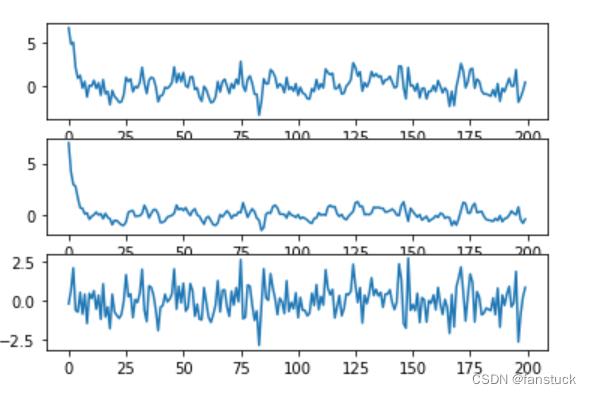 
点关注，防走丢，如有纰漏之处，请留言指教，非常感谢
以上就是本期全部内容。我是fanstuck ，有问题大家随时留言讨论 ，我们下期见。
参阅
平稳时间序列的相关概念_someday or one day的博客-CSDN博客_平稳时间序列
（五十一）时间序列分析二：平稳时间序列分析（ARMA）_小粉桥反手王的博客-CSDN博客_平稳时间序列时间序列模型 （六）：平稳时间序列模型 ：自回归AR 、移动平均 MA 、ARMA 模型_wamg潇潇的博客-CSDN博客_平稳时间序列模型
平稳时间序列_百度百科
自回归模型AR(p)的python实现【案例】_Noema_pku的博客-CSDN博客_python自回归模型
以上是关于ARMA模型性质之平稳AR模型得统计性质的主要内容，如果未能解决你的问题，请参考以下文章
异常检测：综述（基本都是无监督算法）时间序列算法：AR/MA/ARMA传统机器学习算法：孤独森林One Class SVM深度学习算法：AutoEncoderLSTMDeepLog