质数*质数=合数 或者正整数。
质数是除了1和它本身之外,不能被其他数整除的正整数,又称素数。
质数和合数的区别在于因数的个数,质数只有2个因数,合数有多于2个因数。
拓展资料:
质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法:反证法。具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么, 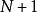 是素数或者不是素数。如果
是素数或者不是素数。如果 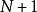 为素数,则
为素数,则 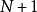 要大于p1,p2,……,pn,所以它不在那些假设的素数集合中。
要大于p1,p2,……,pn,所以它不在那些假设的素数集合中。
如果 为合数,因为任何一个合数都可以分解为几个素数的积;而N和N+1的最大公约数是1,所以不可能被p1,p2,……,pn整除,所以该合数分解得到的素因数肯定不在假设的素数集合中。因此无论该数是素数还是合数,都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说,素数有无穷多个。
其他数学家给出了一些不同的证明。欧拉利用黎曼函数证明了全部素数的倒数之和是发散的,恩斯特·库默的证明更为简洁,哈里·弗斯滕伯格则用拓扑学加以证明。
只有1和它本身两个因数的自然数,叫质数(或称素数)。(如:由2÷1=2,2÷2=1,可知2的因数只有1和它本身2这两个因数,所以2就是质数。与之相对立的是合数:“除了1和它本身两个因数外,还有其它因数的数,叫合数。”如:4÷1=4,4÷2=2,4÷4=1,很显然,4的因数除了1和它本身4这两个因数以外,还有因数2,所以4是合数。)
100以内的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,一共有25个。
质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法:反证法。具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么,N+1是素数或者不是素数。
如果N+1为素数,则N+1要大于p1,p2,……,pn,所以它不在那些假设的素数集合中。
如果N+1为合数,因为任何一个合数都可以分解为几个素数的积;而N和N+1的最大公约数是1,所以N+1不可能被p1,p2,……,pn整除,所以该合数分解得到的素因数肯定不在假设的素数集合中。
因此无论该数是素数还是合数,都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说,素数有无穷多个。
其他数学家给出了一些不同的证明。欧拉利用黎曼函数证明了全部素数的倒数之和是发散的,恩斯特·库默的证明更为简洁,Hillel Furstenberg则用拓扑学加以证明。
任何一个大于1的自然数N,都可以唯一分解成有限个质数的乘积,这里P1<P2<...<Pn是质数,其诸方幂ai是正整数。
这样的分解称为N的标准分解式。
算术基本定理的内容由两部分构成:分解的存在性、分解的唯一性(即若不考虑排列的顺序,正整数分解为素数乘积的方式是唯一的)。
二、输入两个数,判断这个数是否为半质数。
大哈 18:31:05
应该是判断这两个数的积是否为半质数
大哈 18:31:44
半质数的概念:两个质数相乘的积
a``Forget. forget 18:31:54
嗯
大哈 18:34:25
考虑到你循环没学,输入的数可以小点,两个数小于15就行
大哈 18:35:13
题二可以输入两个小于15的数
1 #include <stdio.h>
2
3 int main()
4
5 {
6
7 int a,b;
8
9 printf("请输入两个15以内的数,我将会判断它们的积是否为半质数\n");
10
11 scanf("%d,%d",&a,&b);
12
13 if((a==2||a==3||a==5||a==7||a==11||a==13)&&(b==2||b==3||b==5||b==7||b==11||b==13))
14
15 {
16
17 printf("这两l个数的积为半质数\n");
18
19 }
20
21 else
22
23 {
24
25 printf("这两个数的积不是半质数\n");
26
27 }
28
29 getch();
30
31 return 0;
32
33 }
半质数是什么呢?
数学中,两个素数的乘积所得的自然数我们称之为半素数(也叫双素数,二次殆素数)开始的几个半素数是4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... 它们包含1及自己在内合共有3或4个因子。另外,合数并不一定是半素数,但半素数一定是合数。
半素数在密码学和数论中非常有用,最显著的例子是密码学中的公钥(例如RSA)和随机数发生器。主要的基本原理是利用这类数的与生俱来的难以分解(至少是现在),而且随着数字的增长难度增加。简单的来说,35很容易就可以被分解成5×7,但是要想分解很大的半素数就不是那么容易了。
因此说,我只要判断输入的这两个数是不是质数就行,而||和&&的运用就在这里需要想到了。
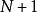 是素数或者不是素数。如果
是素数或者不是素数。如果 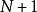 为素数,则
为素数,则 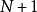 要大于p1,p2,……,pn,所以它不在那些假设的素数集合中。
要大于p1,p2,……,pn,所以它不在那些假设的素数集合中。