粒子滤波简介
Posted Young_Gy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了粒子滤波简介相关的知识,希望对你有一定的参考价值。
粒子滤波基于蒙特卡洛方法,用后验概率中随机抽取的粒子集对目标概率密度函数进行近似。本文将简要介绍如何用粒子滤波进行定位并附上相关代码实例。
粒子滤波概述
粒子滤波,和卡尔曼滤波、一维马尔科夫定位都是贝叶斯滤波的一种方法。其最大特点是原理与实现特别简单。
其核心思想是:用很多个粒子代表定位物体,每个粒子有权重
w
代表该粒子位置的可信度。在prediction阶段,根据物体的控制信息
其步骤图如下,包含下面几个步骤:
- 初始化:用gps初始化粒子群的位置
- prediction:根据motion model与物体的控制信息 u 预测下个时刻粒子群中粒子的位置
- update:根据物体的观测值
z 与地图值 zl 计算出每个粒子的权重 w - resample:根据粒子的
w 重新采样粒子
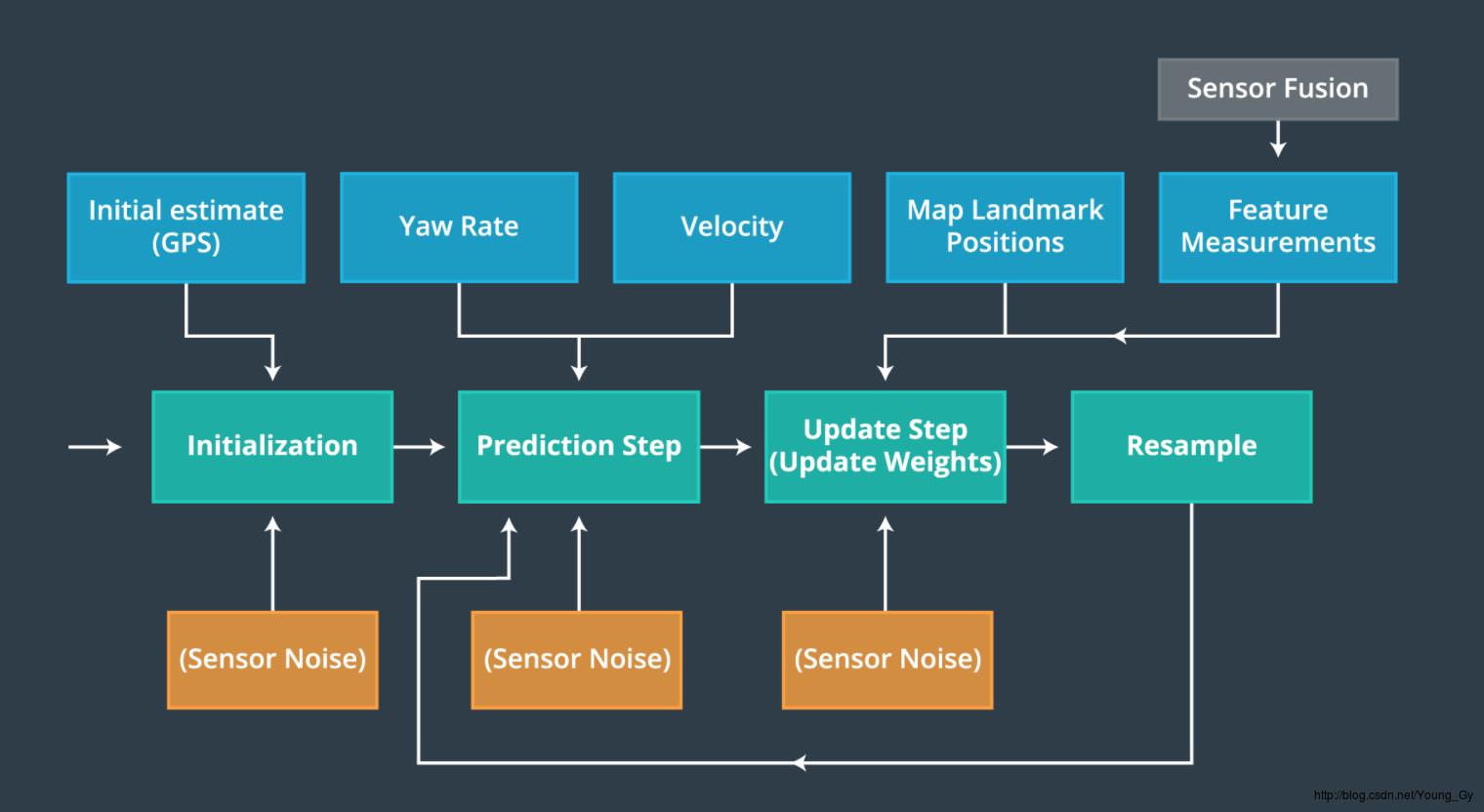
其伪代码如下:

下面,将分阶段具体介绍粒子滤波。
Motion Model
在介绍粒子滤波之前,需要对定位的物体进行建模,我们定位的物体是汽车,使用的模型是Bicycle Model。
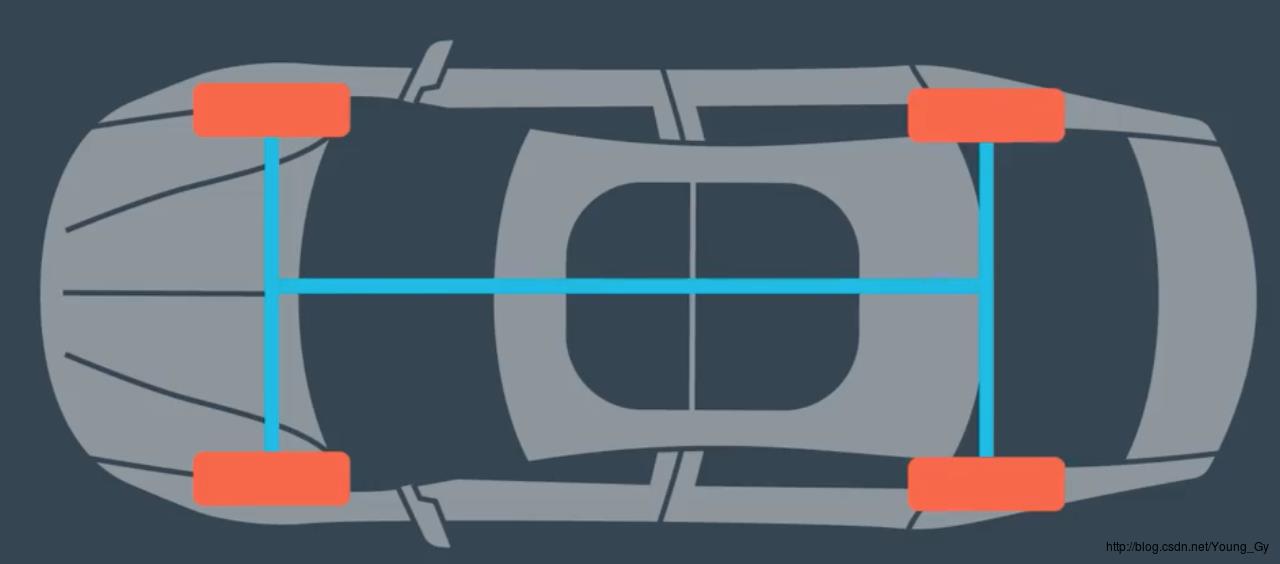
Bicycle Model假定汽车的四个轮子可以简化成一个轮子,类似自行车故得此名。
初始化
初始化较为简单,根据GPS信息对每个粒子初始化即可,需要注意的是初始化的时候需要考虑到GPS的定位误差。
void ParticleFilter::init(double x, double y, double theta, double std[])
// TODO: Set the number of particles. Initialize all particles to first position (based on estimates of
// x, y, theta and their uncertainties from GPS) and all weights to 1.
// Add random Gaussian noise to each particle.
// NOTE: Consult particle_filter.h for more information about this method (and others in this file).
cout<<"Init Start"<<endl;
num_particles = 100;
/*******************************************************
* Set particles
******************************************************/
double std_x = std[0];
double std_y = std[1];
double std_theta = std[2];
// set random engine
normal_distribution<double> dist_x(x, std_x);
normal_distribution<double> dist_y(y, std_y);
normal_distribution<double> dist_theta(theta, std_theta);
for (int i = 0; i < num_particles; ++i)
Particle curr_particle;
curr_particle.id = i;
curr_particle.x = dist_x(gen);
curr_particle.y = dist_y(gen);
curr_particle.theta = dist_theta(gen);
curr_particle.weight = 1.0;
particles.push_back(curr_particle);
/******************************************************
* Set others
******************************************************/
weights.assign(num_particles, 1.0);
is_initialized = true;
cout<<"Weights Size: "<<weights.size()<<endl;
cout<<"Particles Size: "<<particles.size()<<endl;
cout<<"Init Finished"<<endl;
Prediction
Prediction阶段,即:
xt+1=f(xt,ut)
此处根据yaw_rate是否为0分为两种情况,分别是:


代码如下:
void ParticleFilter::prediction(double delta_t, double std_pos[], double velocity, double yaw_rate)
// TODO: Add measurements to each particle and add random Gaussian noise.
// NOTE: When adding noise you may find std::normal_distribution and std::default_random_engine useful.
// http://en.cppreference.com/w/cpp/numeric/random/normal_distribution
// http://www.cplusplus.com/reference/random/default_random_engine/
double std_x = std_pos[0];
double std_y = std_pos[1];
double std_theta = std_pos[2];
normal_distribution<double> dist_x(0, std_x);
normal_distribution<double> dist_y(0, std_y);
normal_distribution<double> dist_theta(0, std_theta);
for (int i = 0; i < num_particles; ++i)
// main
if (fabs(yaw_rate)>0.001)
double theta0 = particles[i].theta;
particles[i].x += velocity/yaw_rate * ( sin(theta0+yaw_rate*delta_t) - sin(theta0) );
particles[i].y += velocity/yaw_rate * ( -cos(theta0+yaw_rate*delta_t) + cos(theta0) );
particles[i].theta += yaw_rate * delta_t;
else
particles[i].x += velocity * delta_t * cos(particles[i].theta);
particles[i].y += velocity * delta_t * sin(particles[i].theta);
// add random noise
particles[i].x += dist_x(gen);
particles[i].y += dist_y(gen);
particles[i].theta += dist_theta(gen);
Update
更新粒子权重的依据是粒子的观测值与地图标志物相似度的高低,越高的话该粒子的权重越大。可是,该过程存在如下问题:
- 粒子观测值的坐标系是以粒子为中心的,粒子前进方向为x轴的坐标系,不同与地图标志物的坐标系。需要统一到地图坐标系。
- 地图的标志物太多,只需要考虑粒子传感器范围内的标志物即可。
- 粒子观测值与地图标志物需要建立一一匹配的关系。
- 更新粒子的权重。
下面,将针对每点分开介绍。
坐标变换
坐标变换,需要求解的问题如下:
(xmap,ymap)=f(xparticle,yparticle,θparticle,xobs,yobs)
在求解该问题之前,引入坐标变换的相关公式:
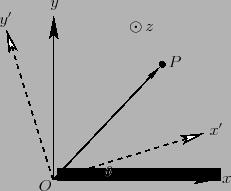
对于上图中的坐标 x,y 到坐标 x′,y′ ,其变换公式如下:
x′y′=xcos(θ)+ysin(θ)=−xsin(θ)+ycos(θ)
对于粒子滤波器中的坐标变换,需要将小车的观测值变换到地图坐标系下粒子的观测值。
记粒子的方向顺时针离水平位置的角度是 θ ,那么从粒子的坐标系到地图的坐标系变换的角度为 −θ ,所以有:
x′y′=xcos(θ)−ysin(θ)=xsin(θ)+ycos(θ)
经过上述公式变换后的坐标是以粒子为圆心,在地图坐标系下的坐标,考虑到粒子的坐标,经过平移变换后可得:
x′y′=xcos(θ)−ysin(θ)+xp=xsin(θ)+ycos(以上是关于粒子滤波简介的主要内容,如果未能解决你的问题,请参考以下文章