概率论小课堂:泊松分布(完善你对随机性的认识,特别是对风险防范的认识)
Posted iOS逆向
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了概率论小课堂:泊松分布(完善你对随机性的认识,特别是对风险防范的认识)相关的知识,希望对你有一定的参考价值。
文章目录
引言
- 伯努利试验:解释了随机事件的发生概率在理论和现实中的差距
- 泊松分布:进一步完善你对随机性的认识,特别是对风险防范的认识。
另一类特殊的伯努利试验,随机事件A发生的概率通常很小,但是试验的次数n很大。
在管理水平和效率相当的情况下,保险这个行业是池子越大风险越小。对于个人来讲,应该优先考虑找那些大保险公司投保。
显然不可能把池子做到无限大,于是在保险行业,就出现了再保险或者保险公司之间互相保险的情况。
I 泊松分布
1.1 概率计算公式
随机事件A发生的概率是p,进行n次独立的试验,恰巧发生了k次,则相应的概率用这样一个公式来计算:
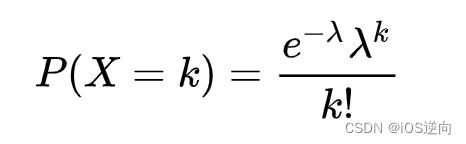
以上是关于概率论小课堂:泊松分布(完善你对随机性的认识,特别是对风险防范的认识)的主要内容,如果未能解决你的问题,请参考以下文章