1457. 二叉树中的伪回文路径

Posted 2023-03-07 Debroon

1457. 二叉树中的伪回文路径

• • 题目
  • 算法设计：深度优先搜索

 

---

题目

传送门：https://leetcode.cn/problems/pseudo-palindromic-paths-in-a-binary-tree/

 

---

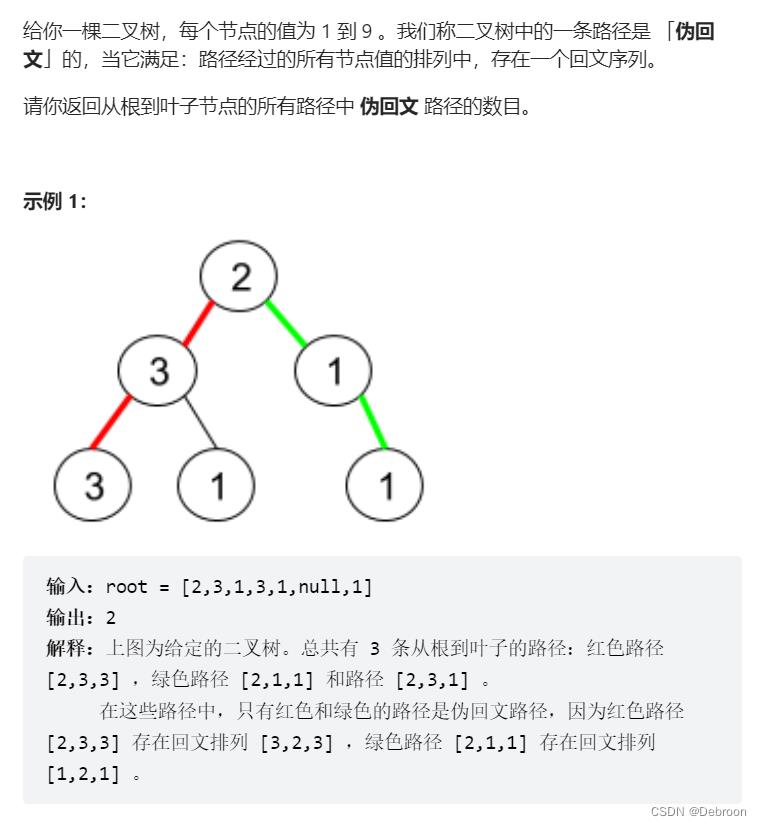
算法设计：深度优先搜索

如何判断一组数字是否存在一个回文串组合？

如 [1, 2, 1]、[2, 1, 1]、[2, 3, 3]、[3, 2, 3]。

规律是：一组数字中，最多一个数字出现的次数为奇数，剩余数字的出现次数均为偶数，这组数字组成一个回文串。

伪回文对，有俩种情况：

• 121，只有 1 个 bit 是 1
• 1221，全部为 0 的情况下是伪回文对。

如果想要构成伪回文串，路径上的至多只能有 1 个奇数数字存在，其他数字都必须是偶数。

因为节点的值只有 1-9，可以用 1bit 表示 1 个数字出现次数是奇数还是偶数，用 9bit 就可以表示 9 个数字出现是奇数还是偶数。

举个栗子：

• 001 000 000，从右往左数，第7位为1，表示数字7出现了奇数次

• 001 000 100，从右往左数，第3、7位为1，表示数字3和7都出现了奇数次。

class Solution 
public:
    int pseudoPalindromicPaths(TreeNode* root, int count = 0) 
        if (!root) return 0;
        count = count ^ (1 << root->val);   
        // 每次遇到元素，就异或。如果该数字个数为奇数，count为1，偶数为0
        // ^：异或让成对数字变0，落单数字不变
        // 1 << n：把 1 左移 n 位，每左移一位就是*2，节点范围是 1-9。作用是位运算存储，第几个数就存到第几位
        
        int res = pseudoPalindromicPaths(root->left, count) + pseudoPalindromicPaths(root->right, count);
        // 非叶子节点返回其子节点的伪回文数
        
        if (root->left == root->right && (count & (count - 1)) == 0) res++;
        // 叶子节点时判断奇偶
        // n & (n-1)：二进制数 n 最后位置的 1 变为 0。
        // 如果只有一个奇数，那奇数操作后会等于0
        // 如果都是偶数0，那偶数操作后还是0
        // 满足条件，伪回文数 + 1
        return res;
    
;