安全多方计算之六：秘密共享

Posted 2023-03-04 机器学习Zero

秘密共享

• 1. 秘密共享简介
• 2. Shamir秘密共享方案
• 3. Asmuth-Bloom方案
• 4. 可验证的秘密共享
• • 4.1 Feldman的VSS方案
  • 4.2 Pedersen的VSS方案
• 5. 无分发者的随机秘密共享

1. 秘密共享简介

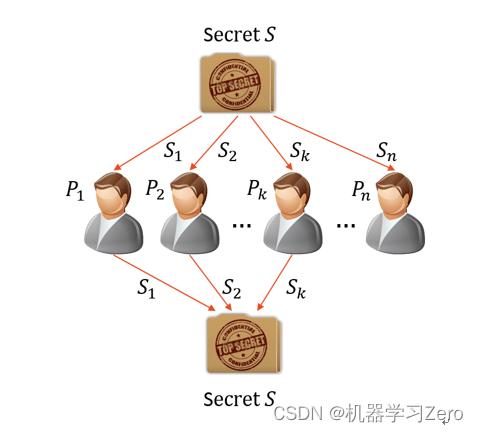
秘密共享通过将秘密以适当的方式拆分，拆分后的每一个份额由不同的参与者管理，单个参与者无法恢复秘密信息，只有若干个参与者一同协作才能恢复秘密消息。

秘密共享定义如下：秘密持有者$S$需要将原始秘密$m$在参与者集合中$P_1,P_2,...,P_n$分享，$S$分发给$P_1$子秘密$m_{p_i}$，使得只有特定参与者的集合才能够从他们的子秘密中恢复秘密$m$，而其他参与者不能得到秘密$m$的任何信息。

能够计算出秘密$m$的参与者集合$P$的一个子集$A\subseteq P$，称为一个授权子集。令$\Gamma$为所有授权子集构成的集合，则称$\Gamma$访问结构。

秘密共享方案一般描述如下：将共享的秘密$m$分割成$n$个子秘密，并将其分发至$n$个参与者，使得授权子集$\Gamma$中的参与者可共同恢出复秘密$m$，而非授权子集中的参与者无法得到关于秘密$m$的任何信息。

2. Shamir秘密共享方案

Adi Shamir于1979年提出了基于拉格朗日(Lagrange)插值定理的$(t,n)$-门限方案。该方案利用有限域上的次随机多项式来分享秘密，被分享的秘密为多项式的零次系数，恢复秘密至少需要t个多项式上的点。

方案描述如下：

设 $GF(q)$ 是一个有限域, $q$为公开大素数, 共享的密钥 $k\in GF(q)$, 可信中心给 $n(n<q)$个共享者 $P_i(1\le i\le n)$ 分配共享的过程如下:

(1) 秘密分发

可信中心随机选取多项式 $f(x)=a_{t-1}{x}^{t-1}+\dots +a_2{x}^2+a_{1}x+a_0\in$ $GF(q)[x]$, 常数 $a_0=k$ 为要分享的秘密。

可信中心在 $GF(q)$ 中选择 $n$ 个非零的互不相同的 元素 $x_1,x_2,\dots ,x_n$, 计算 $y_i=f\left(x_i\right),1\le i\le n$, 将子密钥 $\left(x_i,y_i\right)$ 分配给共享者 $P_i(x_i$ 是公开的, $y_i$ 为 $P_i$ 的秘密共享)。

（2） 秘密重构

给定 $t$ 个共享 $y_{i_s}(1\le s\le t)$, 从Lagrange多项式重构的

f ( x ) = ∑ s = 1 t y i s ∏ j = 1 , j ≠ s t x − x j x i s − x i j , k = a 0 = f ( 0 ) = ∑ s = 1 t y i s ∏ j = 1 , j ≠ s t − x j x i s − x i j = ∑ s = 1 t b s y i s , \\beginaligned & f(x)=\\sum_s=1^t y_i_s \\prod_j=1, j \\neq s^t \\fracx-x_jx_i_s-x_i_j, \\\\ & k=a_0=f(0)=\\sum_s=1^t y_i_s \\prod_j=1, j \\neq s^t \\frac-x_jx_i_s-x_i_j=\\sum_s=1^t b_s y_i_s, \\endaligned ​f(x)=s=1∑t​yis​​j=1,j=s∏t​xis​​−xij​​x−xj​​,k=a0​=f(0)=s=1∑t​yis​​j=1,j=s∏t​xis​​−xi区块链BaaS云服务（14）华大BGI区块链“安全多方计算“

区块链BaaS云服务（24）边界智能 IRITA平台

安全多方计算-介绍

安全多方计算 同态密文计算 零知识证明 是什么对比优缺点

第162篇 笔记-安全多方计算

门限签名技术火了，它的硬核之处绝不仅仅是秘密共享……