浅谈单神经元网络PID控制算法

Posted 2023-03-02 争取35岁退休

---

本文仅用作记录学习单神经元网络PID控制算法过程的心得体会及个人理解，若有错误，欢迎指正！

传送门

• 神经网络
• • 神经网络的三个主要构成
  • 神经元
• 单神经元网络PID控制算法
• • 增量式
  • 位置式
  • 神经元的输入
  • 神经元网络的输出u(k)
  • • 神经元激励函数$f$
    • 控制律u(k)
  • 学习规则
  • • 无监督Hebb学习规则
    • 有监督Delta学习规则
    • 有监督Hebb学习规则
    • 单神经元PID控制器的学习规则
  • Matlab仿真实例
  • • 增量式单神经元PID控制算法
    • 位置式单神经元PID控制算法
    • 对比分析讨论
    • 单神经元PID控制器中的参数整定
• 总结
• 更新补充

---

神经网络

关于神经网络的背景定义等诸多概念，网上有很多更权威详细的解析。这里不多赘述。

这里建议阅读维基百科关于人工神经网络的描述 维基百科-人工神经网络

神经网络的三个主要构成

1. 结构 （Architecture）
   结构指的是网络中的变量和它们的拓扑关系，一般情况下，神经网络具有多层网络以及由多神经元相互链接组成。一种常见的多层结构的前馈网络结构主要是由以下三部分组成：

   • 输入层（Input layer），众多神经元（Neuron）接受大量非线形输入消息。输入的消息称为输入向量。
   • 输出层（Output layer），消息在神经元链接中传输、分析、权衡，形成输出结果。输出的消息称为输出向量。
   • 隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（控制系统在一定结构、大小等的参数摄动下，维持某些性能的特性）更显著。习惯上会选输入节点1.2至1.5倍的节点。

   这种网络一般称为感知器（对单隐藏层）或多层感知器（对多隐藏层），神经网络的类型已经演变出很多种，这种分层的结构也并不是对所有的神经网络都适用。

2. 激励函数 （activation function）
   大部分神经网络模型具有一个短时间尺度的动力学规则，来定义神经元如何根据其他神经元的活动来改变自己的激励值。一般激励函数依赖于网络中的权重（即该网络的参数）。

3. 学习规则 （Learning Rule）
   学习规则指定了网络中的权重如何随着时间推进而调整。这一般被看做是一种长时间尺度的动力学规则。一般情况下，学习规则依赖于神经元的激励值。它也可能依赖于监督者提供的目标值和当前权重的值。学习规则主要有以下几种分类：

   • 监督式学习网络（Supervised Learning Network）为主
   • 无监督式学习网络（Unsupervised Learning Network）
   • 混合式学习网络（Hybrid Learning Network）
   • 联想式学习网络（Associate Learning Network）
   • 最适化学习网络（Optimization Application Network）

神经元

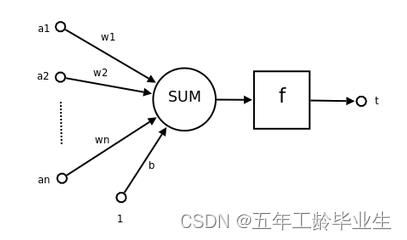
其中，$a_1$-$a_n$为输入向量的各个分量；$w_1$-$w_n$为神经元各个突出的权重值；$b$为神经元的激励偏置；$f$为神经元的传递函数，也就是前面提到的激励函数；$t$为神经元的输出；其满足以下关系：
$$t=f(\overrightarrow{W^{{}^{\prime }}\stackrel{⃗}{A}}+b)$$

在维基百科中提到，单个神经元的作用为：把一个n维向量空间用一个超平面分割成两部分（称之为判断边界），给定一个输入向量，神经元可以判断出这个向量位于超平面的哪一边。

单神经元网络PID控制算法

了解上面部分关于神经网络的内容之后，已经基本满足学习单神经元PID的内容。单神经元PID顾名思义，并没有明显的网络结构，仅一个单独的神经元参与控制计算。
优化本质：向神经元输入各项变量，神经元根据输入权重、输入量数值以及激励函数来计算控制律增量$\Delta u$，根据学习规则来迭代优化输入权重，以此往复使损失函数达到最小。

1. 优化目标
   在讨论单神经元PID控制算法时，要首先明确算法优化的目标对象，并顺着这个方向去找到优化方法以及评估优化的数学标准。
   在$PID$控制算法中，影响控制器性能及响应特性的参数就是三个环节的系数$k_p$，$k_i$，$k_d$。由于传统$PID$控制算法属于线性控制算法，因此在遇到强扰动或者被控对象非线性特性明显时，无法实现高的控制性能。也就是说，传统$PID$控制算法在遇到不同的场景不同的系统状态时刻，有着对应的不同的最优$PID$参数。
   因此，我们的优化目标是，使控制网络能够自己判定在当前扰动以及当前系统状态下，自身控制器的最优参数是多少，并通过不断迭代优化来达到一个最优的效果。

任务一完成：寻找优化目标，$K_p$，$K_i$，$K_d$

2. PID控制算法
   PID控制算法主要分两种类型，位置式和增量式子，二者的控制律$u(k)$分别为。
   • 位置式
     $$u(k)=K_p\ast error(k)+K_i\ast \sum _{z=1,2,...k}^{n}error(z)+K_d\ast (error(k)-error(k-1))$$
   • 增量式
     $$\Delta u(k)=u(k)-u(k-1)\Rightarrow \Delta u(k)=K_p\ast (error(k)-error(k-1))+K_i\ast error(k)+K_d\ast (error(k)-2error(k-1)+error(k-2))$$
     从表达式来看，二者同根同源，最终的控制律$u(k)$计算相同。只不过位置式有积分项，而增量式无积分项，对于一些不同的开发场景有着各自的优缺点。

对于这两种PID控制算法表达形式，哪一种更加适合加入单神经元来实现新的控制算法。

这个问题在我刚学习单神经元控制算法时就已经产生，带着这个疑问翻阅相关资料以及查询网上相关帖子，要么忽略过，要么是搪塞而过。另外很想吐槽的一点是，现在网上很多人喜欢把别人的文章搬到其他论坛上发表，导致一个现象就是搜索了很多不同的帖子，内容却十分相似，有的甚至一字不差。

在此分享一篇写的很好的相关文章 相关文章

它对于为什么是增量表达式的问题描述是这样的

此图仅作为依据材料，无其他用意，侵删

这里是对于这个问题的个人理解就，无论是位置式还是增量式的PID控制算法，其本质都是对被控对象的误差进行响应，是典型的线性闭环负反馈控制器。因此在PID控制器中加入单神经元，其控制器的形式不变，整个神经网络控制器的输入依然是被控对象的误差集（例如误差时间序列或误差累加结果），输出依然是对被控对象的控制律(control law)u(k)。对于位置式和增量式不同的是，其输入到神经元的变量的内容以及其激励函数的形式不同，究其本质是一致的。具体细节继续看后续的讨论。

回到正题，我们已经明确了优化的目标就是三个环节的参数，因此将这三个参数作为神经元三条输入突触的三个权重系数，而输入对象就是该环节的输入量。

增量式

$$\Delta u(k)=K_p\ast (error(k)-error(k-1))+K_i\ast error(k)+K_d\ast (error(k)-2error(k-1)+error(k-2))$$令三个输入权重系数分别为$w_1=K_p$，$w_2=K_i$， w 3 = K