51nod 1632概率与期望B君的连通

Posted 2023-02-27 SSL_ZZL

B君的连通

• 题目
• 解题思路
• Code

51nod 1632 B君的连通

---

题目

B国拥有n个城市，其交通系统呈树状结构，即任意两个城市存在且仅存在一条交通线将其连接。A国是B国的敌国企图秘密发射导弹打击B国的交通线，现假设每条交通线都有50%的概率被炸毁，B国希望知道在被炸毁之后，剩下联通块的个数的期望是多少？

输入
第一行输入一个数n（2<=n<=100000）
接下来n-1行，每行两个数x,y表示城市x,y间有一条交通线。(1<=x,y<=n)
数据保证其交通系统构成一棵树。
输出
输出一个数，表示答案乘2^(n-1)后对1,000,000,007取模后的值。
输入样例

3
1 2
1 3

输出样例

8

---

解题思路

一条边不删产生期望 1
每删去一条边，都会分成两半（?），就是联通分块数量 +1 ，而炸掉这条边的概率为 0.5 ，产生期望为 0.5 * 1 = 1
一共 n - 1 条边，E = 1 + 0.5 (n - 1)
最后答案乘 2 ^ (n - 1)
ans = 2 ^ (n - 1) * (1 + 0.5 (n - 1) )

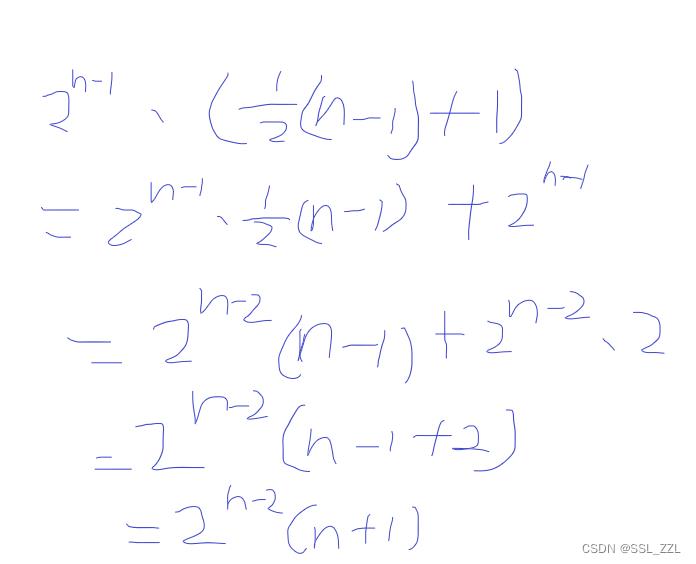
字有点丑。。
化简得ans = 2 ^ (n - 2) * (n + 1)

---

Code

#include <bits/stdc++.h>
#define P 1000000007
#define ll long long

using namespace std;

ll n, ans;

int main() 
	scanf("%lld", &n);
	ans = n + 1;
	for(int i = 1; i <= n - 2; i ++)
		ans = ans * 2 % P;
	printf("%lld", ans % P);