爬虫反爬:JS逆向实战2
Posted 阿呆攻防
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了爬虫反爬:JS逆向实战2相关的知识,希望对你有一定的参考价值。
爬虫反爬:JS逆向实战2
1. 简介
学习某度翻译的JS参数逆向,我们可以来看看某道翻译的,用作一个练手项目即可,这一次我们要新增一个学习内容就是用Python将其复现出来获取到我们需要的数据,主要的还是JS逆向过程中的方法的学习。
2. 实战信息
网址:
aHR0cHM6Ly9mYW55aS55b3VkYW8uY29tLw==
接口:
aHR0cHM6Ly9mYW55aS55b3VkYW8uY29tL3RyYW5zbGF0ZV9vP3NtYXJ0cmVzdWx0PWRpY3Qmc21hcnRyZXN1bHQ9cnVsZQ==
逆向参数:
-
salt: 16574297023827
-
sign:ce2ff90e8f7715308bc304fa261942ea
-
lts:1657429702382
-
bv:c66136bfe956af5cdec6ce6da806f86e
3. 实战流程
第一步是永远不变的抓包找接口,有了上一个项目的实战经验,我们可以直接找到我们需要的接口,并且设置一个XHR断点,在接口可以被断住的情况下,XHR断点是迅速找到调用方法位置的断点方式,先看看需要逆向的参数。
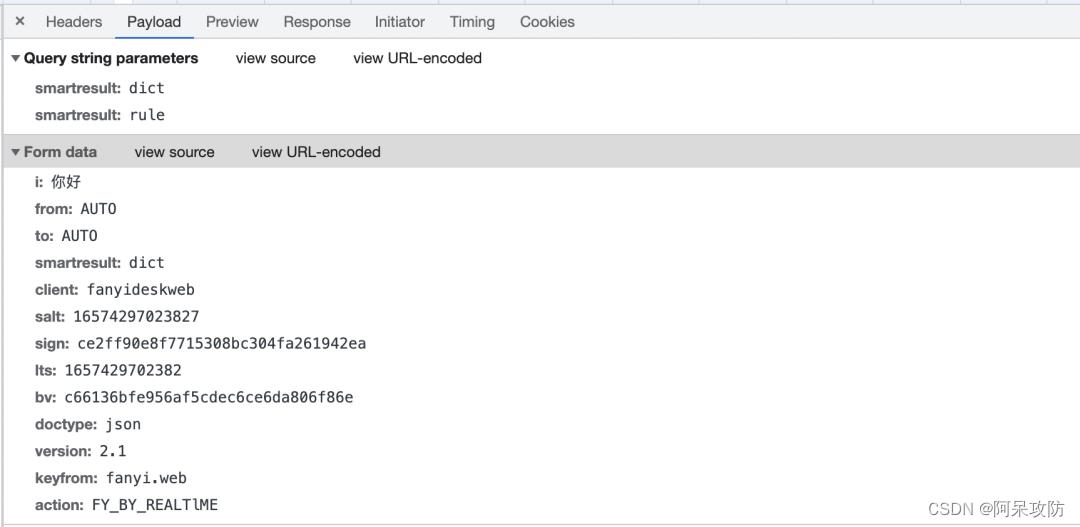
salt、sign、lts、bv都像是需要逆向的参数,然后设置"/translate_o"XHR断点开始调试。
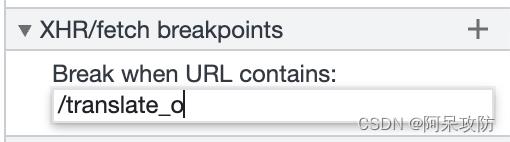
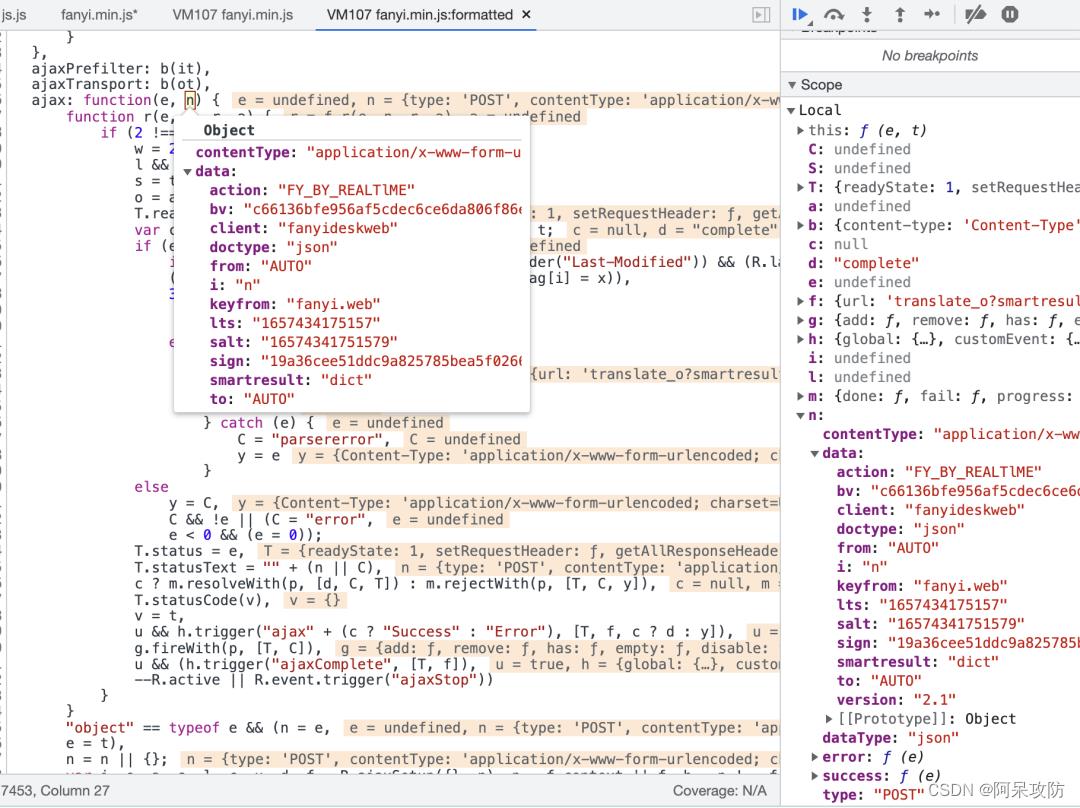
通过作用域快速找到n是传入的对象,往上一级调用栈中去寻找n参数传入位置,最后在此处发现这个对象,下断后重新开启一个调试。
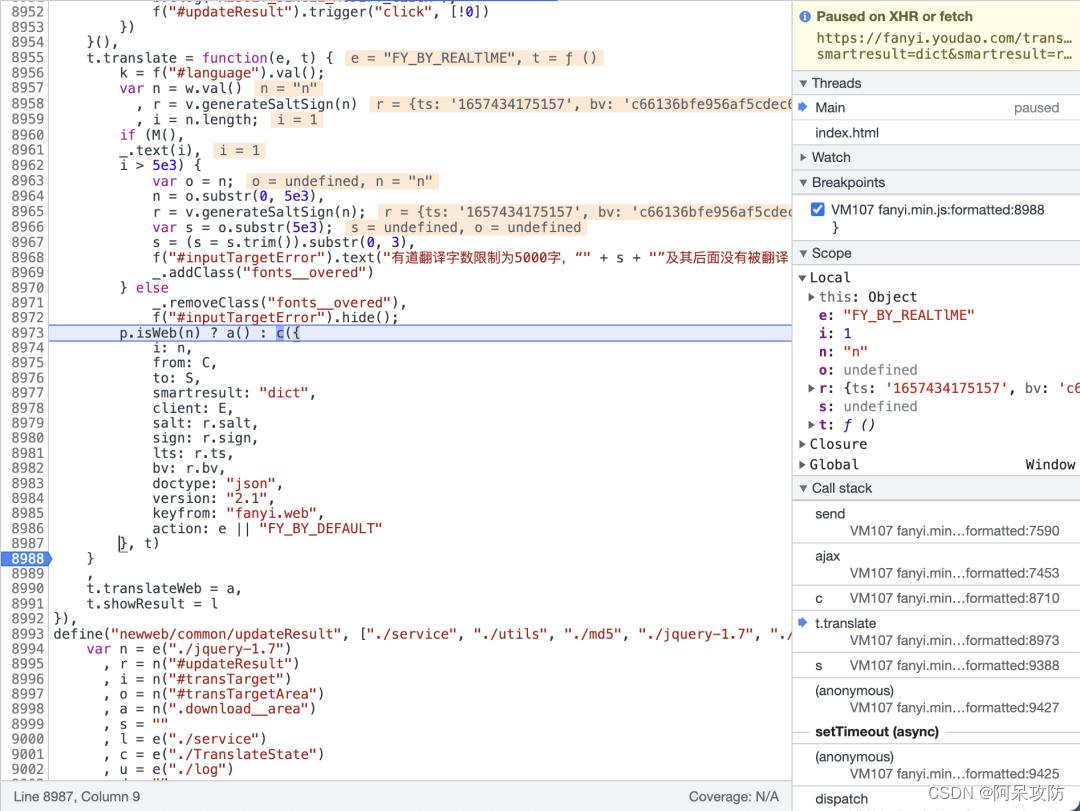
可以看到四个需要逆向的加密参数均是r对象产生r在上文中是v.generateSaltSign(n)产生所以这个即为加密的方法,先测试数据。
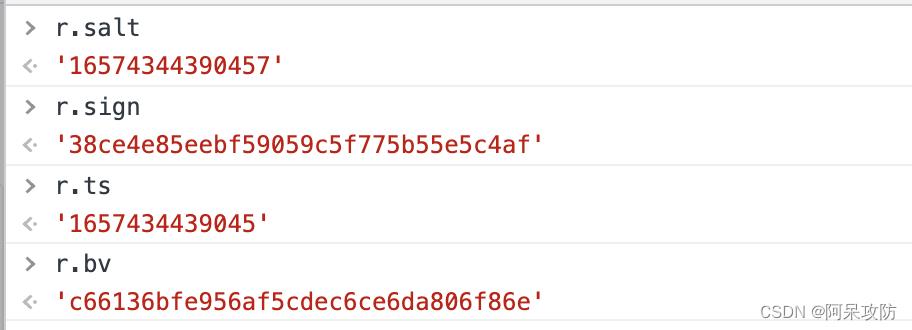
确定之后,进入生成加密数据的方法generateSaltSign()

可以看到bv是由n.md5()方法对navigator.version处理后得到,navigator.version在一个网站中是不会变的等会抠代码的时候直接替换就好了,ts是一个时间戳,salt是时间戳加一个随机数,sign是拼接后的二次加密。
首先通过三方测试一下是否经过魔改的md5,如果没有魔改的话,可以直接调用Node中的方法实现或者用python单独实现,当然也是可以抠的,先测试一下。
"5.0 (Windows NT 6.3) AppleWebKit/537.36 (Khtml, like Gecko) Chrome/101.0.4951.54 Safari/537.36 Edg/101.0.1210.39"
直接进入MD5方法,抠下来改写成一个方法即可,目前是一个对象里的属性方法。

function md5(e)
var t, n, i, o, a, s, m, g, v, y = Array();
for (e = h(e),
y = f(e),
s = 1732584193,
m = 4023233417,
g = 2562383102,
v = 271733878,
t = 0; t < y.length; t += 16)
n = s,
i = m,
o = g,
a = v,
s = l(s, m, g, v, y[t + 0], 7, 3614090360),
v = l(v, s, m, g, y[t + 1], 12, 3905402710),
g = l(g, v, s, m, y[t + 2], 17, 606105819),
m = l(m, g, v, s, y[t + 3], 22, 3250441966),
s = l(s, m, g, v, y[t + 4], 7, 4118548399),
v = l(v, s, m, g, y[t + 5], 12, 1200080426),
g = l(g, v, s, m, y[t + 6], 17, 2821735955),
m = l(m, g, v, s, y[t + 7], 22, 4249261313),
s = l(s, m, g, v, y[t + 8], 7, 1770035416),
v = l(v, s, m, g, y[t + 9], 12, 2336552879),
g = l(g, v, s, m, y[t + 10], 17, 4294925233),
m = l(m, g, v, s, y[t + 11], 22, 2304563134),
s = l(s, m, g, v, y[t + 12], 7, 1804603682),
v = l(v, s, m, g, y[t + 13], 12, 4254626195),
g = l(g, v, s, m, y[t + 14], 17, 2792965006),
m = l(m, g, v, s, y[t + 15], 22, 1236535329),
s = c(s, m, g, v, y[t + 1], 5, 4129170786),
v = c(v, s, m, g, y[t + 6], 9, 3225465664),
g = c(g, v, s, m, y[t + 11], 14, 643717713),
m = c(m, g, v, s, y[t + 0], 20, 3921069994),
s = c(s, m, g, v, y[t + 5], 5, 3593408605),
v = c(v, s, m, g, y[t + 10], 9, 38016083),
g = c(g, v, s, m, y[t + 15], 14, 3634488961),
m = c(m, g, v, s, y[t + 4], 20, 3889429448),
s = c(s, m, g, v, y[t + 9], 5, 568446438),
v = c(v, s, m, g, y[t + 14], 9, 3275163606),
g = c(g, v, s, m, y[t + 3], 14, 4107603335),
m = c(m, g, v, s, y[t + 8], 20, 1163531501),
s = c(s, m, g, v, y[t + 13], 5, 2850285829),
v = c(v, s, m, g, y[t + 2], 9, 4243563512),
g = c(g, v, s, m, y[t + 7], 14, 1735328473),
m = c(m, g, v, s, y[t + 12], 20, 2368359562),
s = u(s, m, g, v, y[t + 5], 4, 4294588738),
v = u(v, s, m, g, y[t + 8], 11, 2272392833),
g = u(g, v, s, m, y[t + 11], 16, 1839030562),
m = u(m, g, v, s, y[t + 14], 23, 4259657740),
s = u(s, m, g, v, y[t + 1], 4, 2763975236),
v = u(v, s, m, g, y[t + 4], 11, 1272893353),
g = u(g, v, s, m, y[t + 7], 16, 4139469664),
m = u(m, g, v, s, y[t + 10], 23, 3200236656),
s = u(s, m, g, v, y[t + 13], 4, 681279174),
v = u(v, s, m, g, y[t + 0], 11, 3936430074),
g = u(g, v, s, m, y[t + 3], 16, 3572445317),
m = u(m, g, v, s, y[t + 6], 23, 76029189),
s = u(s, m, g, v, y[t + 9], 4, 3654602809),
v = u(v, s, m, g, y[t + 12], 11, 3873151461),
g = u(g, v, s, m, y[t + 15], 16, 530742520),
m = u(m, g, v, s, y[t + 2], 23, 3299628645),
s = d(s, m, g, v, y[t + 0], 6, 4096336452),
v = d(v, s, m, g, y[t + 7], 10, 1126891415),
g = d(g, v, s, m, y[t + 14], 15, 2878612391),
m = d(m, g, v, s, y[t + 5], 21, 4237533241),
s = d(s, m, g, v, y[t + 12], 6, 1700485571),
v = d(v, s, m, g, y[t + 3], 10, 2399980690),
g = d(g, v, s, m, y[t + 10], 15, 4293915773),
m = d(m, g, v, s, y[t + 1], 21, 2240044497),
s = d(s, m, g, v, y[t + 8], 6, 1873313359),
v = d(v, s, m, g, y[t + 15], 10, 4264355552),
g = d(g, v, s, m, y[t + 6], 15, 2734768916),
m = d(m, g, v, s, y[t + 13], 21, 1309151649),
s = d(s, m, g, v, y[t + 4], 6, 4149444226),
v = d(v, s, m, g, y[t + 11], 10, 3174756917),
g = d(g, v, s, m, y[t + 2], 15, 718787259),
m = d(m, g, v, s, y[t + 9], 21, 3951481745),
s = r(s, n),
m = r(m, i),
g = r(g, o),
v = r(v, a);
return (p(s) + p(m) + p(g) + p(v)).toLowerCase()
然后把方法调用扣下来,可是方法里面依赖套依赖所以要抠全,所以从md5方法调用上方找到的依赖方法全抠,不用分析。
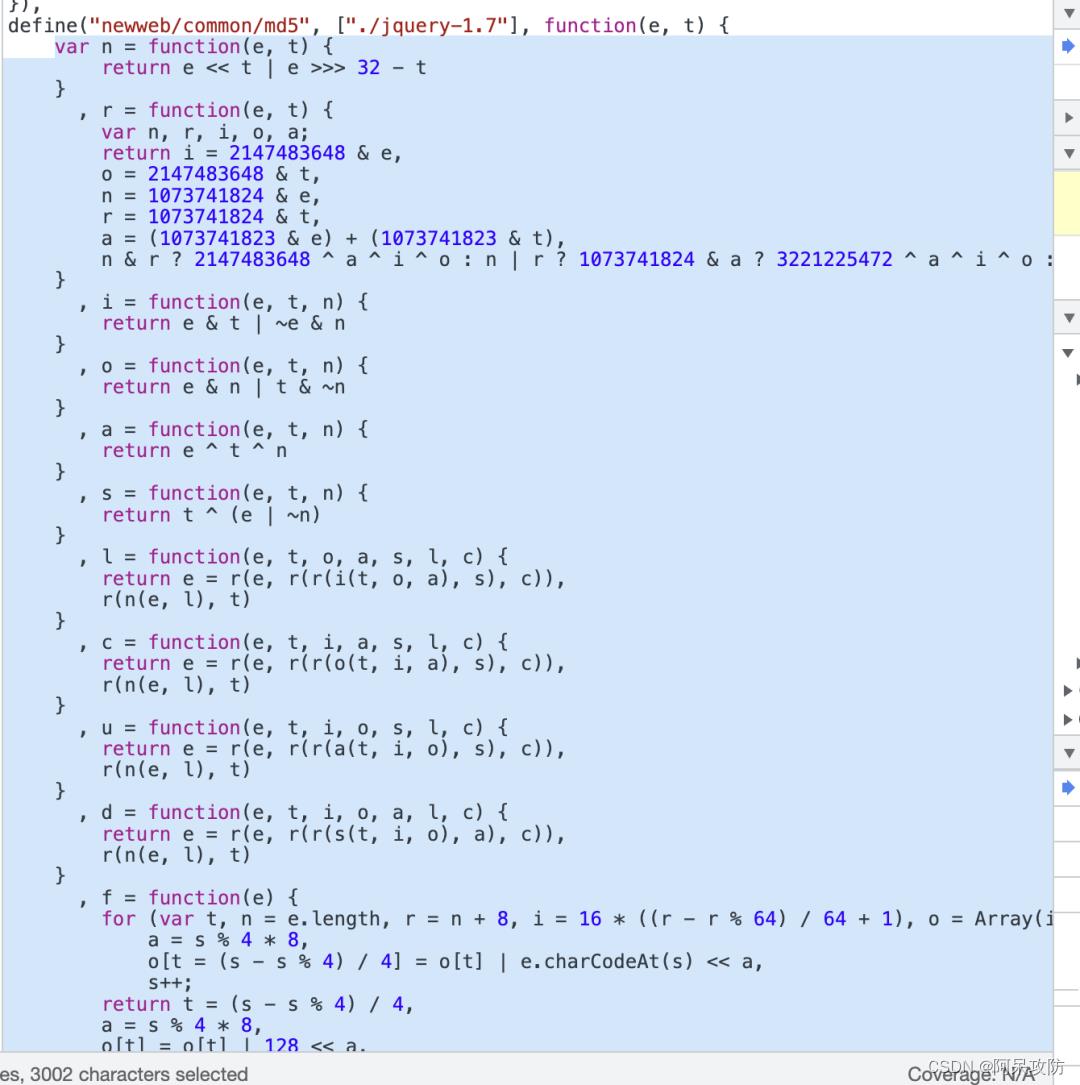
直接扒下来的完整代码测试bv的结果为:

对比一致即为成功。

自行构造一个变量导出即可Node的方法要求module.exports
var bv = md5("5.0 (Windows NT 6.3) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/101.0.4951.54 Safari/537.36 Edg/101.0.1210.39")
var ts = "" + (new Date).getTime()
var salt = ts + parseInt(10 * Math.random(), 10)
function getBv()
return bv
function getTs()
return ts
function getSalt()
return salt
function getSign(e)
return md5("fanyideskweb" + e + salt + "Ygy_4c=r#e#4EX^NUGUc5")
module.exports =
getBv,
getSalt,
getSign,
getTs
即可成功复现。
4. JS完整代码
// md5依赖
var n = function (e, t)
return e << t | e >>> 32 - t
, r = function (e, t)
var n, r, i, o, a;
return i = 2147483648 & e,
o = 2147483648 & t,
n = 1073741824 & e,
r = 1073741824 & t,
a = (1073741823 & e) + (1073741823 & t),
n & r ? 2147483648 ^ a ^ i ^ o : n | r ? 1073741824 & a ? 3221225472 ^ a ^ i ^ o : 1073741824 ^ a ^ i ^ o : a ^ i ^ o
, i = function (e, t, n)
return e & t | ~e & n
, o = function (e, t, n)
return e & n | t & ~n
, a = function (e, t, n)
return e ^ t ^ n
, s = function (e, t, n)
return t ^ (e | ~n)
, l = function (e, t, o, a, s, l, c)
return e = r(e, r(r(i(t, o, a), s)