论文笔记Leveraging Line-point Consistence to Preserve Structures for Wide Parallax Image Stitching

Posted 2023-02-05 spearhead_cai

论文链接：https://openaccess.thecvf.com/content/CVPR2021/papers/Jia_Leveraging_Line-Point_Consistence_To_Preserve_Structures_for_Wide_Parallax_Image_CVPR_2021_paper.pdf

代码链接：https://github.com/dut-media-lab/Image-Stitching

摘要

生成具有自然结构的高质量拼接图像是计算机视觉中的一项具有挑战性的任务。在本文中，我们成功地保留了宽视差图像的局部和全局几何结构，同时减少了伪影和失真。投影不变量特征数用于匹配输入图像的共面局部子区域。这些匹配良好的子区域之间的单应性产生一致的线和点对，抑制重叠区域中的伪影。我们探索并将全局共线结构引入到一个目标函数中，以指定和平衡图像变形所需的特征，这可以在减轻失真的同时保留局部和全局结构。考虑到人类视觉对线性结构的敏感性，我们还开发了综合的拼接质量的综合测量方法，来量化点的共线性和匹配线对的差异。大量实验通过呈现清晰的纹理并在拼接图像中保留突出的自然结构，证明了所提出的方法优于最先进的方法。特别是，我们的方法不仅表现出较低的错误，而且在所有测试图像中的差异最小。

---

1.介绍

图像拼接，将多个图像组合成具有更宽视野的更大图像[25]，广泛用于摄影测量[24]、机器人导航[6]和智能手机全景[29]。为最先进的技术生成高质量的拼接图像仍然具有挑战性，因为它们会遭受严重不愉快的影响，例如伪影和失真，尤其是对于宽视差图像。

特征匹配是对齐多个图像以产生无伪影拼接的关键，因为匹配的特征充当对齐的锚。 SIFT 特征 [23] 广泛用于许多传统的特征点检测和匹配方法 [4, 5, 30]。最近的一些工作还引入了线特征，以在点容易失配的大视差和/或低纹理的情况下获得稳健的匹配[11]。林等人。在目标函数中通过不同的权重利用点和线特征[16]。不幸的是，这些方法分别匹配点和线，因此当不可避免地发生不匹配时，局部周围区域可能会不一致且不均匀地拉伸或压缩，从而在拼接图像中呈现伪影。廖等人。采用RANSAC策略通过使用图像之间的单应性来细化点和线对[17]。值得注意的是，单应关系仅适用于同一投影平面内的点和线[12]。因此，那些对单应性但忽略共面约束的改进无法给出准确的匹配。如图1中前三行红色矩形所示，右侧放大的重叠区域显示了相框、时钟和计算机上的伪影。探索共面区域并细化相应的点和线匹配对是非常可取的。

图像拼接必须保留线性结构，同时减轻失真，因为人类视觉感知对这些结构非常敏感。 as-projective-as-possible (APAP) 方法采用局部约束的参数扭曲 [30]，但会遭受严重的形状扭曲，尤其是在非重叠区域，如图 1 中第一行的蓝色矩形所示。保形半投影 (Sphp) [4] 和全局相似性先验 (GSP) [5] 具有相似的想法，可以为不同的图像区域调整不同的扭曲。测地线保留[13]和线结构保留[3]涉及共线性保留，但它们的图像调整大小以一张全景图像作为输入，已经包含正确的全局几何结构作为参考。最近，廖等人提出单视角扭曲（SPW）[17]来保护线性结构，同时抑制扭曲。这些方法可以很好地保留局部结构，但在同时维护局部和全局线性结构时无法解决冲突。全局共线结构可以是横跨图像主要部分的一条长线，例如图 1 中两个图片帧下方的长线，也可以是几个单独的共线线段。当前的线检测器 [26] 无法检测或连接这些长线。因此，通过设置适当的参数可以很好地保留局部形状，但在图 1 的第二行中全局线性结构变形。在第三行中，保留线性结构会导致局部形状严重失真。保留局部和全局共线结构仍然没有解决。

同时，现有评价拼接质量的指标还不够全面。这些指标包括匹配点之间的距离 [30] 和像素强度局部模式上的平均几何误差 (SSIM) [27] 只能量化点匹配的性能。它们都不能反映线性结构上点的对齐或匹配线段的共线性。定量评估图像拼接线性结构的保存也是一个悬而未决的问题。

本文利用线和点的一致性来保留线性结构，这些线性结构是图像拼接的基本几何形状。我们将输入图像划分为线邻域上的共面区域，并使用一系列反映线和点固有性质的几何不变量来匹配来自不同视图的区域。因此，这些共面区域之间的单应性可以准确地生成线和点的匹配。随后，设计了用于warp的线引导目标函数以保留局部和全局线性结构并抑制失真。图 1 中的第四行表明我们的方法显着提高了图像质量。此外，为了更全面地分析拼接图像的质量，提出了一种线条的定量评价方法。我们的贡献总结如下：
• 我们设计了一种新的匹配策略，通过使用射影不变量探索共面子区域来获得一致的点和线对。这种匹配遵循基本的共面要求用于单应性，以便它可以提供准确的预对齐，同时消除伪影和非均匀失真。
• 据我们所知，我们是第一个将全局共线结构合并为显着减轻非自然扭曲的约束。
• 我们提出了一个综合度量来量化图像拼接的线性结构的保存。

我们将提出的方法与最先进的具有挑战性的自然图像对进行比较，具有突出的线性结构，涵盖相机运动、场景和视野的变化。我们的方法可以产生视觉上吸引人的拼接，我们的点匹配平均 RMSE 比 SPW [17] 低 31%。同时，我们的方法最准确、最稳定，可以根据所提出的度量来保留线性结构。第 3、4 和 5 节分别阐述了我们的贡献。

2. 相关工作

本文提出了同时保留局部和全局结构的线引导图像拼接方法。因此，本节回顾了以前与扭曲相关的工作，以减少失真和具有线结构约束的扭曲。

传统的拼接方法通常为每个输入图像估计一个最优的全局变换。它们仅适用于理想的近平面场景，并且生成的图像通常会受到局部伪影和投影失真的影响 [2]。因此，一些方法试图使扭曲适应图像的不同区域。林等人[21]提出了一种平滑变化的仿射（SVA）变换，以实现更好的局部适应。李等人使用贝叶斯模型去除异常值和用于分析扭曲的薄板样条[14]。高等人将图像分为地平面和远平面，并提出双单应扭曲（DHW）[8]来减少失真。保形半投影（SPHP）扭曲[4]结合了重叠和非重叠区域的投影变换。 Adaptive as-natural-as-possible (AANAP) warps [18] 有类似的想法，将重叠区域的单应变换转换为整个图像。赫尔曼等人[9]引入多个配准以获取更高的准确性，而不是单个配准。李等人。提出了一种准单应性（QH）扭曲[15]，它依赖于全局单应性，同时挤压非重叠区域。但是，它们不够灵活，无法减少视差较大的场景的失真。

为了获得更好的对齐和更少的失真，APAP [30] 微调全局单应性扭曲以适应位置相关的对齐。陈等人通过最小化由对齐、局部和全局相似性项组成的能量函数，提出了一种基于全局相似性先验 (GSP) 的扭曲 [5]。他们的方法旨在解决非重叠区域的失真，但线性结构没有得到很好的保护。张等人通过设置一系列先验约束和手动指导来获得更好的性能[32]。林等人考虑到像素强度的差异，这在低纹理图像中效果很好[20]。李等人将图像分割成超像素，并根据视差场景的翘曲残差使用计算出的特征匹配来自适应地翘曲它们[12]。

此外，还有一些基于接缝的方法可以减少局部失真。提出了一种容忍视差的扭曲，它结合了单应性和内容保留扭曲（CPW）[22]来控制失真[31]。然而，他们的方法仍然会导致大视差的形状失真。Lin 等人。通过自适应特征加权迭代地改进接缝引导的局部对齐，并引入了一个新术语来保留显着线结构方法[19]。然而，非重叠区域仍然存在全局失真。

为了实现更好的拼接质量，减少失真并保留线性结构，Li 等人将线特征引入图像拼接，通过引入线性对齐项[16]来改进内容保留扭曲。向等人提出了一种具有全局相似性约束的线引导局部扭曲[28]。廖等人同时强调单视角扭曲的不同特征，包括对齐、扭曲和显着性 [17]。然而，全局共线结构很少被解决，并且在这些方法中仍然存在局部和全局结构保持之间的冲突。

3. 基于点线约束一致性进行预对齐

在本节中，设计了一种基于双特征（线和点）的预对齐算法，如图 2 所示。

• 首先，基于在线检测将图像划分为共面子区域，其中一个如图 2 所示 的绿色矩形。
• 然后，通过从一系列射影不变量计算的相似度来匹配子区域。
• 第三，增加和细化匹配点对，通过匹配区域之间的单应性匹配线。
• 最后，基于双重特征构建全局预对齐。

3.1 基于线检测的子区域划分

共面区域之间的局部单应性比全局单应性更准确。 由于多条线是由平面相交形成的，我们粗略假设，由线长确定的邻域可以看作是图像的局部共面子区域。利用LSD[26]得到原图线段，然后根据梯度方向将线的邻域分为左侧和右侧，因为位于线不同侧的点可能不共面。 一条线的梯度定义为它上面所有点的平均梯度。 如图 3 所示，在一条直线的附近，任何一个像素点到直线的距离都小于 α·len(l)，并且到垂直平分线的距离小于 β·len(l)。 在我们的实验中，α 和 β 分别设置为 2.0 和 0.5 [10]。

3.2 基于点线不变性的子区域匹配

​ 为了匹配共面的子区域，最终匹配更多的线点对，引入投射不变特征数(CN)来构造线-点不变量，并在此基础上定义子区域之间的相似度。 CN 定义如下：

​ 令 K 为域，$P^m$(K) 为 K 上的 m 维投影空间，$P_i{}_{i=1,2,...,R}$ 为 $P^m$(K) 中构造闭环的不同点（ $P_{R+1}=P_1$)。 在线段 $P_i{P}_{i+1}{}_{i=1,2,...,R}$ 上有不同的点$Q^{(j)}{}_{i=1,2,...,S}$ ，每个点 $Q_i^{(j)}$ 可以由 $P_i$ 和 $P_{i+1}$ 线性表示为 $Q_i^{(j)}=a_i^{(j)}{P}_i+b_i^{(j)}{P}_{i+1}$。 令 $P=P_i{}_{i=1,2,...,R}，Q=Q_i^{(j)}{}_{i=1,2,...,R}^{j=1,2,...,S}$，则该量称为 P 和 Q 的特征数

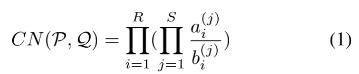
​ 由于 CN 的构造需要一个闭环并且每条边上的点数相等，因此我们使用五个点来构造一个三角形，并且每条边上都有相等的交点 [10]。 如图2左上图所示，$K_l^1$ 和 $K_l^2$ 是红线 l 上的两个端点。 $P_1,P_2,P_3$ 是直线同一侧的三个非共线特征点，用红点标记。 任意三个点（$K_l^1,K_l^2,P_1,P_2,P_3$）不共线。

​ 我们用两个点 $P_i,P_j$ 表示一条直线，即 $\overline{P_i{P}_j}$，然后两条直线 $\overline{P_i{P}_j},\overline{P_k{P}_m}$ 的交点表示为 $<\overline{P_i{P}_j},\overline{P_k{P}_m}>$。我们可以获取几个相交点（蓝色点），包括