ID-GNN解读

Posted 2023-02-03 让AI服务于我

1.Mp-GNN

在解读ID-GNN之前，了解MP-GNN模型是有必要的。我在这里假设你们是知道图的一些基础知识，包括什么是点，什么是边，以及熟悉一些基本的Embedding。我们考虑自然语言处理的时候也是将词通过embedding表示成向量然后去完成一些机器学习和深度学习的任务。我们着眼于节点分类，并且不考虑边的权值。也是将节点embedding成向量，通过图神经网络信息的会聚来更新节点的表示，最后我们可以通过其他的线性层识别类别，结合简单的交叉熵损失函数来进行训练。
我们分析下面这个图：

首先考虑第0层，各个节点被初始化embedding。在第一层的时候，每个节点的向量可以被自身和邻居节点的向量通过一定的消息传递更新。这样不断的加深GNN层，可以使每个节点的邻居的邻居的······的信息相互隐含。通俗的讲，就是不断通过邻居更新自己的向量，又作为其它节点的邻居是更新其他节点的向量。通过图的连通性达到信息的汇聚。

MP-GNN的缺陷

MP-GNN看上去是一个非常简单的结构，其中消息的传递可以通过MLP，这样一个简单的三层神经网络去计算邻居节点的信息并加和来更新自己的信息。常见的消息传递的过程函数如下：

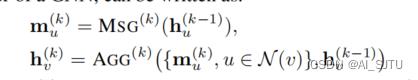
上标（k）表示的是第k层GNN，mu表示v的邻居u通过传递它上一层也就是k-1层的表示得到的新的信息。然后通过第二个公式将v的所有邻居节点u以及自身上一层的向量表示聚合得到新的表示。

MP-GNN的表达力上限

学术界使用1-WL test来衡量一个图的表达力，很遗憾MP-GNN的表达力未能超越1-WL test。那么什么是1-WL test。下面给出了区别两个GPL（图表示学习）示例的1-WL test伪代码。

核心：是将每个节点的向量表示映射为一一对应的颜色。通过邻居节点的颜色和自身的颜色通过不断的迭代去更新，在更新的过程中，检查两个图在初始化embedding相同的情况下对应节点是否得到了不一样的表示来区分两个图是否是相似的。然而即便两个图通过一定层数的迭代得到的结果依旧相同却也无法进行区分。接下来我们看具体的示例。

我以左中右来命名图中的三个子图，我们可以观察到在左面的子图中，v1和v2的计算图也就是下面对应的以其各自为根节点的信息汇聚的树结构是相同的。因为每个节点都有两个邻居节点。在这样一种情况下，我们明知道v1和v2应该属于不同的类别亦或者说他们的聚类系数是不同的。然而通过MP-GNN和1-WL test都无法进行区分。同理，在中间的子图中，我们知道v1和v2经过MP-GNN计算得到的embedding是一样的。但是在我们进行链接预测任务时，其各自与v0节点的距离是无法把控的，也就是说MP-GNN并不能捕获距离信息。在右面的子图中，两个结构属于属性正则图。属性正则图是指汇聚了一类节点，在这一类节点中，每个点的表示以及邻居个数是相同。我们细看每一个节点的计算图发现他们是一致的，即便他们在视觉上存在差异。所以如何解决呢？

颜色身份信息注入

ID-GNN考虑到了以上的问题，通过给节点注入颜色信息解决以上问题。


我们将节点A和节点B注入相同颜色信息，其他非颜色节点使用相同的embedding向量。即便如此，我们发现在以上的任务中，v1和v2的计算图将不再相同。解决了节点标识的问题，如何进行消息传递呢？

异质消息传递

通常啊，MP-GNN所有的节点采用相同的MSG 函数进行消息的传递。这样其实我们直观上去看，可以发现会在一定程度上丢失节点的颜色信息。所以呢，作者使用异质消息传递，针对不同的节点采取了不同的消息传递函数。注意：作者是以着色节点为中心为其设计了单独的msg函数，为不是其邻居。我们要思考这是什么？我们拿下面的图举例：

第一种按照作者的设计，我们可以让着色节点的邻居更加明显的区分其是否和着色节点相邻，因为着色节点通过不同的msg传递给自己信息。如果我们是将着色节点的邻居以单独的msg传递，而非着色节点的邻居是另一个msg传递。这样会有一个问题，就是非着色节点并不能很好的区分它的邻居是否是着色节点。以正方形右上角的节点为例，着色节点和非着色节点以相同的msg传递给自己，这样会导致其并不能区分谁是着色节点。我们知道了ID-GNN的思想，那么它是如何具体实现的呢？

ID-GNN的算法

EGO（v,k)表示以v为中心的一个k跳得到的子图。

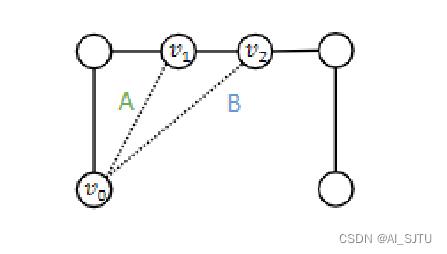
我们假设以v1为中心节点，那么1跳就包含了

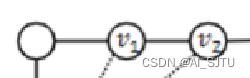
两跳就包含了

我们得到了一个EGO以后，具体看算法。算法是针对图中的每个节点都找到了一个EGO，针对EGO中的节点，使用K层GNN来更新其表示。更新的过程用到了异质消息传递，如前面提到的。得到了ID-GNN，那我们能用其做什么呢？

ID-GNN的应用

• ID-GNN的作者们证明了一个非常nb的结论，至今都没有想明白，因为作者未在论文提供相关的证明。
  
  翻译过来就是得到的节点表示的第j个维度代表了以该节点为起点和终点的一个长度为j的环的数量。这样有一个好处就是可以计算聚类系数。聚类系数的公式如下：

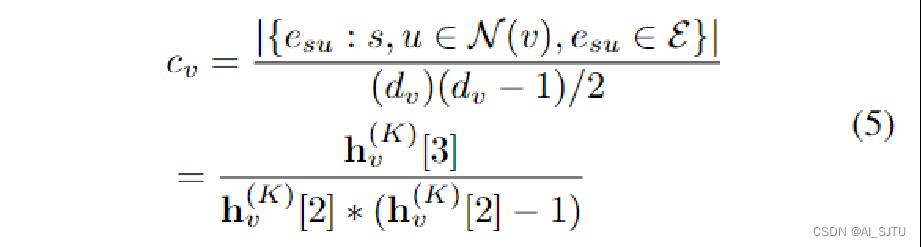
其实翻译过来就是以该节点为三角形的一个顶点的三角形的数量和度之间的一种度量。分母Hv(K)[3]毫无争议就是三角形的数量，而Hv（K）[2]代表了度可能有一些人不能理解，长度为二的环无非是两个节点形成的环，在有向图里面很直观。而在无向图中，我们可以将一个无向边拆分成两个有向边。

• 计算两个节点的可达性
  其实我们学过数据结构的话，是知道有很多算法来解决这类问题的，比如DFS,BFS。那如何通过GNN去计算呢，作者给出了对应的msg和agg。
  
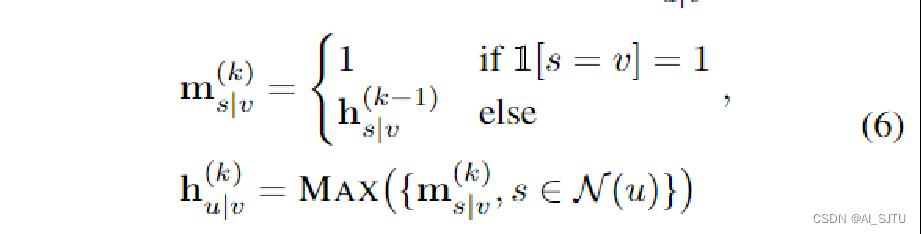
  每个节点的初始表示h为0，是一个数值，每个节点的表示非0就是1，就两种表示可能。我们把这个消息传递过程带入到前面的EGO，我们探求u和v之间是否可达，那么更新就是看u的邻居是否可到v来更新就可以了。以下面这个图为例：
  
  我们知道处理更新的顺序是无关的，我们看v1和v0之间是否可达，那么首先更新v1发现不可达，但是在第二层GNN时，v0和v1之间的节点标记为可达也就是1，那么在更新v1时也是可达。

ID-GNN Fast

每个节点使用环的计数作为增强节点特征来注入身份信息。那么如何得到每个顶点长度为k的环的数量呢？
正解：Diag(A^k)[v]就是顶点v的对应的长度为k的环的数量。如何理解：

我们知道矩阵的乘积是每一行与每一列相乘，矩阵中的每个元素的意义是如果Vi和Vj是相邻的就是1，否则为0.其中自身和自身默认是不可达的。也就是A的对角线元素为0。那么我们在计算乘积时会发现得到的结果矩阵A^2，就是每个节点i通过一跳到达另一个节点又跳到j的路径个数，对角线元素就代表回到自身的环的数量。得到了这个矩阵其实我们在回到之前的问题，如何找到节点i和节点j是否可达时又多了一个新的方法。但是我们知道矩阵的乘积为O（n3)，所以要根据具体的任务去决定使用哪种方法更适合。
本文到这里就结束了！